【深度学习】从实现异或运算开始
最近读到一本书,源码很清晰。结合之前自己的理解,想就此记几篇随笔,搬运在此,也方便后来查阅。
故事从单层感知器无法实现“异或”运算开始。
当感知器(Perception)第一次被提出时,作为发明者的罗森布拉特(Rosenblatt)霎时间受到了广泛的赞誉,但他的反对者以其无法解决“异或”问题为由,使得这个日后成为神经网络中最基本的神经元模型遭遇了人工智能发展史上的第一次寒冬,罗森布拉特也因此积郁而终。当时,罗森布拉特不知道的是,多层感知机就能解决以“异或”问题为代表的非线性问题,他更不知道的是,日后深度学习所采用的深度神经网络是如何带火了一批智能应用的出现。当然,当时没有找到针对多层神经网络进行训练的机制是卡住了进步的关键,随着反向传播(Backpropagation,BP)算法的提出,神经网络展现出面对复杂非线性问题强大的回归和分类能力。
单层感知器为什么无法实现“异或”运算
这要从单层感知器的结构谈起,即它本质上是一个 线性单元。
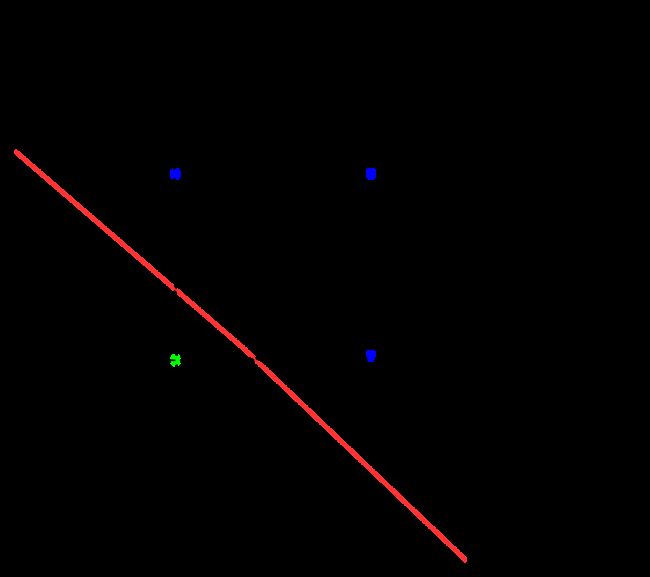
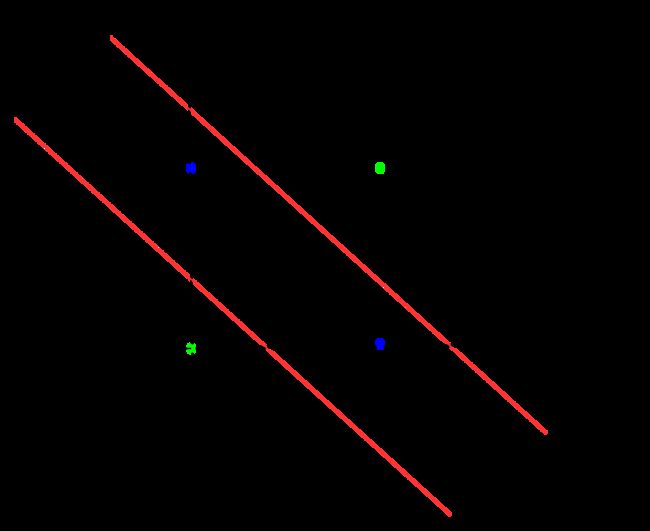
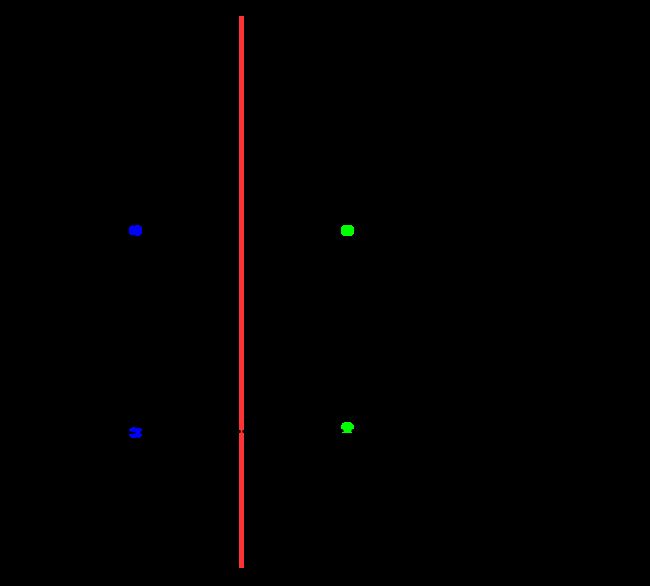
在平面中,针对“与”“或”“非”问题,我们都能画出一个线性的超平面对问题进行区分。但对于“异或”问题,我们无法找到这样一个线性的超平面,或者说:它至少需要两条分界线。
以二元为例,从数学公式上我们可以这样简要证明:假设存在一个这样线性的超平面,则
{ w 1 + θ > 0 ( 1 ) w 2 + θ > 0 ( 2 ) θ < 0 ( 3 ) w 1 + w 2 + θ < 0 ( 4 ) \left\{ \begin{aligned} w_1+ \theta > 0 &&(1) \\ w_2+\theta > 0 &&(2) \\ \theta< 0 &&(3) \\ w_1+w_2+\theta < 0 &&(4) \end{aligned} \right. ⎩ ⎨ ⎧w1+θ>0w2+θ>0θ<0w1+w2+θ<0(1)(2)(3)(4)
综合(1)-(3),我们可以得到
{ w 1 + θ > 0 w 2 > − θ > 0 ⇒ w 1 + w 2 + θ > 0 \left\{ \begin{aligned} w_1+\theta>0 \\ w_2 > -\theta >0 \end{aligned} \right. \Rightarrow w_1+w_2+\theta>0 {w1+θ>0w2>−θ>0⇒w1+w2+θ>0
而这显然与(4)是相矛盾的,即不存在这样一个线性的超平面。
两层感知机实现"异或"运算
通过PyTorch,我们利用两层神经网络来实现对"异或"运算的模拟(笔者因为cuda版本不适配,未用与源码一致的GPU加速,而是直接在CPU上进行了训练)。
我们先需要构造的是四个输入输出关系对,即
x = [[0,0],[0,1],[1,0],[1,1]]
y = [[0],[1],[1],[0]] # 用列表构建输入和输出
之后我们再搭建一个两层的神经网络,即
net = nn.Sequential(
nn.Linear(2,20), # 全连接层,2个输入,20个输出
nn.ReLU(), # ReLU激活函数层
nn.Linear(20,1), # 全连接层,20个输入,1个输出
nn.Sigmoid() #Sigmoid 激活函数层
)
接下来就是正常的训练过程。训练的全流程代码如下:
import torch
import torch.nn as nn # 导入torch模块和nn模块
x = [[0,0],[0,1],[1,0],[1,1]]
y = [[0],[1],[1],[0]] # 用列表构建输入和输出
x_tensor = torch.tensor(x)
y_tensor = torch.tensor(y) # 将列表转换成Tensor变量
x_tensor = x_tensor.float()
y_tensor = y_tensor.float()
net = nn.Sequential(
nn.Linear(2,20), # 全连接层,2个输入,20个输出
nn.ReLU(), # ReLU激活函数层
nn.Linear(20,1), # 全连接层,20个输入,1个输出
nn.Sigmoid() #Sigmoid 激活函数层
)
print(net) # 输出网络结构,也可以去掉
optimizer = torch.optim.SGD(net.parameters(), lr = 0.05) # 设置优化器
loss_func = nn.MSELoss() # 设置损失函数,均方误差函数
for epoch in range(5000): # 训练部分
out = net(x_tensor) # 实际输出
loss = loss_func(out, y_tensor) # 实际输出和期望输出传入损失函数
optimizer.zero_grad() # 清除梯度
loss.backward() # 误差反向传播
optimizer.step() # 优化器开始迭代
if epoch % 1000 == 0: # 每1000epoch显示
print(f'迭代次数:{epoch}') # 输出迭代次数
print(f'误差:{loss}') # 输出损失函数的输出值
out = net(x_tensor)
print(f'out:{out.data}') # 输出训练到最后的结构
torch.save(net,'net.pkl') # 保存整个网络模型
看得出来,在4000次训练后,误差已经缩小为了仅为2‰。其中保存的”net.pkl"文件即是我们训练得到的网络,其中包括了网络的结构(如层数)和其权重。
接下来,我们加载已经训练好的模型并输入一组参数(0,1)进行验证。过程如下:
import torch # 导入torch模块
x = [[0,1]]
x_tensor = torch.tensor(x) # 设置输入
x_tensor = x_tensor.float() # 将Tensor变量转换成FloatTensor类型,直接传入CPU
net = torch.load('net.pkl') # 加载保存的网络模型
out = net(x_tensor) # 将输入传入网络得到输出
# out = out.cpu() # 将输出从GPU传入CPU
outfinal = out.data # 取输出的数据
if outfinal > 0.5: # 判断输出结果是否大于0.5,决定最终输出
outfinal = 1
else:
outfinal = 0
print(f'out={outfinal}') # 输出最终输出
可以发现out=1,与预期结果一致,读者也可以验证其他输入。“麻雀虽小五脏俱全”,尽管这仅是一个简单的“异或”运算,但读者可以从中一窥神经网络学习的基本流程,而我认为这正是这个例子的精妙之处。