【4】循环神经网络的直观理解

引子

  人类不会每时每刻都从头开始思考。正如你在阅读这篇文章的时候，你会根据前面出现的词语，来思考后面的每一个词语的含义。换句话说，你的大脑不会把之前阅读到的信息“扔掉”，而是将它们“存储”下来，用于对后续词语的理解。
  然而，传统的神经网络（也包括前面说的CNN），并不能做到这一点，这可是一个挺大的缺点。比如说，你想对电影中下一秒将会发生的事件进行预测，你该怎么做呢？目前还不清楚传统的神经网络如何利用它对电影中先前事件的来推理出后面将发生的事件。
  循环神经网络解决了这个问题。字面上理解，它是神经网络中存在循环的的网络，它最大的特点就是，允许信息持续存在，即信息持久化。下面咱们赶紧来看看RNN的神奇之处吧！

1. 序列数据

  RNN是一种擅长对序列数据进行建模的神经网络，为了理解这句话的含义，咱们先充分发挥一下想象力，假设有一颗小球正在朝某个方向运动，你刚好抓拍了一张小球的照片，如下图所示：

  如果你想预测球移动的方向，那么仅仅根据屏幕上方的信息，你该怎么做呢？恐怕仅仅根据这么一条信息，你也只能凭空猜测了。

  因此我们需要收集更多小球在不同时刻的位置信息， 这样才能做出一个有效的预测，如下所示：

  上面的例子，主要是解释了什么样的数据是序列数据，即数据之间存在着一个特定的顺序，一条数据紧紧跟随着上一条数据，有了这些信息，你现在可以看到球向右移动。

  我们所说的序列数据，根据不同的序列，表现出多种不同的形式。如音频数据是一种自然序列， 你可以把下方的音频频谱图切成有序的小块，然后输入RNN。

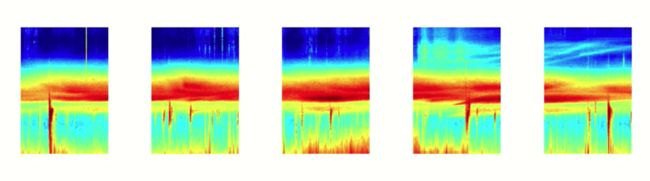
  文本就是另一种形式的序列了，你可以将文本划分成一系列的字符或一系列单词。

2. 顺序存储

  根据上面的说明，我们知道了RNN擅长处理序列数据，但是它是怎样实现的呢？

  实际上，RNN实现这个功能，主要是使用了顺序存储的概念，接下来我们再通过一个例子，来直观感受一下顺序存储的作用。

  我想请你在脑海中读一遍二十六个字母表：

   这个对你而言应该不难，毕竟现在的小孩们都会唱这个字母表，那么现在请你试着倒着读一遍字母表：

   哈哈，我打赌这个肯定比之前那个要吃力点吧~

   再来一个有趣的，从字母F开始，在脑海中读出后面剩下的字母表。

   我想，作为一个普通人，你一开始肯定会比较艰难的思考F之后到底是哪几个字母，终于回想起G、H、I、J、K、L、M、N之后，你的大脑又找到了之前的记忆，剩下的就又能很快的记起来了。

  经过上面的例子，我们可以直观的感受到，我们人类在学习字母表的时候，是把它当作一个序列来学习的，因此在按照顺序来记忆的时候，我们能很快找到字母之间的模式。顺序存储可以让我们的大脑更容易识别出序列中隐藏的模式。

3. 循环神经网络

  所以，上面说到的RNN中，主要体现了一个顺序存储的设计理念，那到底RNN是怎么实现顺序存储的呢？我们先举一个前馈神经网络的例子看看。

  我们如何让前馈神经网络能够使用先前的信息来影响后来的信息呢？如果我们在神经网络中增加一个可以传递先前信息的循环会怎么样？

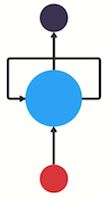
  实际上，上图就是循环神经网络的本质。RNN中有一个循环机制，充当一条信息高速公路，让信息可以从一个步骤流向下一个步骤，如下图所示：

  这个信息，指的是隐藏状态，它代表着神经网络中，早先输入的数据，那我们接下来通过一个RNN的用例，来更进一步地理解它的循环机制吧！

  假设我们想要构建一个聊天机器人，它的功能是可以根据用户输入的文本，来判断用户的意图，实现下图所示的效果：

  为了解决这个问题，我们可以分成“两步走策略”。

  （1）我们把输入的文本用RNN进行编码；
  （2）我们把上一步生成的编码，喂给一个前馈神经网络，实现分类任务的训练与预测；

  假设用户输入：$whattimeisit?$ 首先，我们将句子分解成单个的词语。因为RNN是按照顺序进行训练的，所以我们每次只能输入一个单词。

  我们第一步是把 $What$ 喂给RNN，经过编码后，输出一个中间结果。

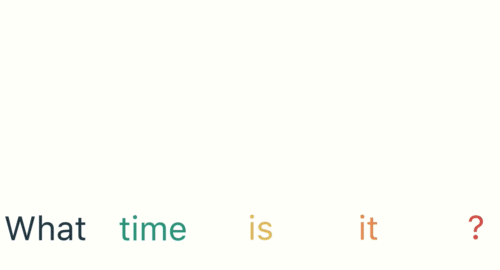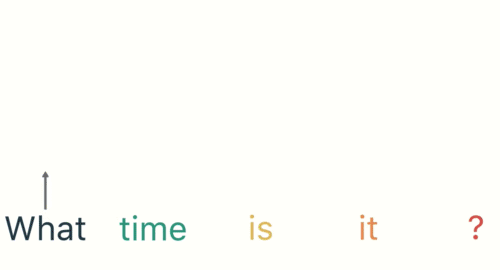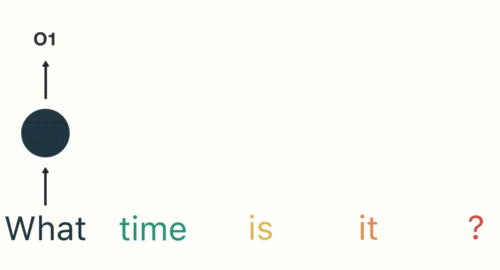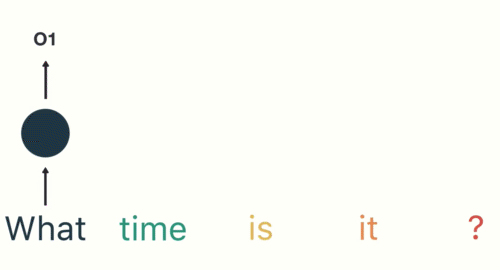
  在第二步中，我们把 $time$ 这个单词喂给 RNN，除了这个输入之外，还有上一步中的生成的中间结果（hidden state）。即此时的输入包含了 $What$ 和 $time$ 两个信息，然后再产生一个中间结果。

  重复上面的这个过程，直到最后一步。

  在最后一步中，你可以发现，此时 RNN 编码了前面所有输入的单词的信息，只不过每个单词的权重大小不一样（根据颜色判断）。

  最后一步中，RNN模型最后的输出 05，就是我们将序列数据编码后的最终结果，然后将它喂给前馈神经网络进行分类训练！

  俗话说，$Talkischeap,showmeyourcode.$ 我们可以将上述的流程，用一个简单的代码进行展示。

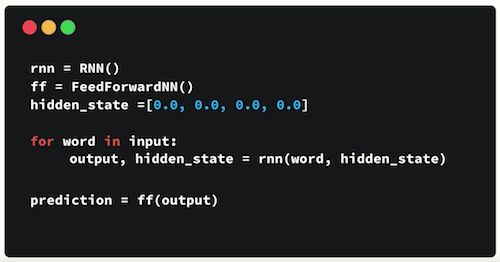
  我们来对上述代码逐行进行解读。

1. 前面两行分别初始化了两个神经网络，一个是循环神经网络，另一个是前馈神经网络；
2. 之后我们初始化了一个全为 0 的隐藏状态向量，它的维度由你的循环神经网络来决定；
3. 遍历输入的每一个单词，把当前单词和当前的隐藏状态向量传给RNN网络进行训练，训练完之后，返回一个输出结果和更新后的隐藏状态向量，我们发现 hidden_state 每一轮都会更新，然后喂给RNN模型；
4. 遍历完所有输入的单词之后，我们得到一个编码了全部输入信息的输出值output，这个 output 就是我们前馈神经网络的输入，然后得出最终的分类结果；

4. 梯度消失

  前面有简单提到过，RNN 最终输出的结果，有着不同比例的颜色分布，它其实是用来揭示 RNN 最大的弱点，短期记忆(short-term memory)问题.

  我们观察上图可以发现，在最后的输出中，$What$(黑色部分) 和 $time$(绿色部分) 这两个词的信息几乎不存在。短期记忆和梯度消失都是由于反向传播的性质引起的，我们知道现在训练神经网络的算法，基本是都是用的BP算法，接下来我们来看看反向传播对深度前馈神经网络的影响。

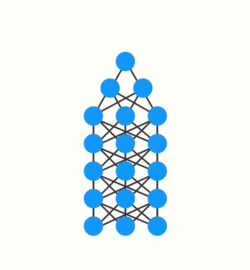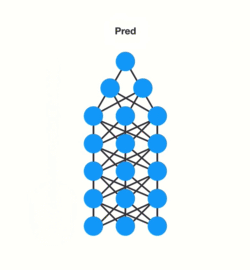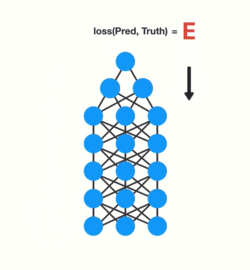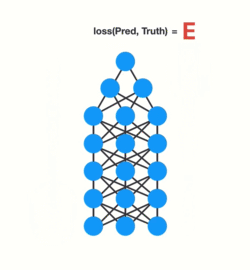
  我们都知道，梯度被用来调整神经网络中每一层的权重矩阵的值。梯度越大，权重参数的调整也就越大越大，反之亦然，这也就是问题所在。

  在进行反向传播时，层中的每个节点根据其前一层中的梯度效果来计算当前层的梯度值。也就是说，如果上一层中对权重的调整很小（梯度值较小），那么梯度对当前层的调整就会更小，这进而会导致梯度在向后传播时呈指数级收缩。由于梯度极小，内部权重几乎没有调整，因此层数较小的权重矩阵无法进行任何学习，这也被称作梯度消失。

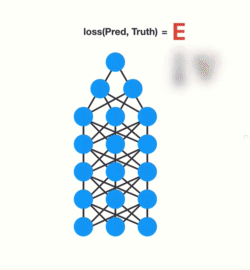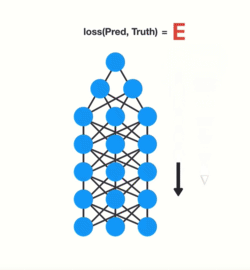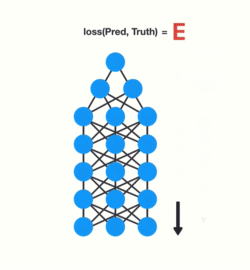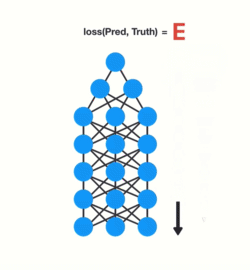
  这个性质也适用于循环神经网络，你可以将循环神经网络中的每个时间步骤视作一个网络层，为了训练一个循环神经网络，你使用了一种被称作 back-propagation through time (简称BPTT)的反向传播算法，它的梯度值在每一个时间步骤中以指数级收缩。

  由于梯度消失的问题，传统的RNN不能够跨越时间步骤学习到早期的信息。这意味着在尝试预测用户的意图时，有可能不会考虑 $What$ 和 $time$ 这两个词。然后网络就可能作出的猜测是 $“isit？”$。

  很明显，这个输入十分模糊，即使是人类也很难辨认这到底是什么意思。因此，如果我们不能解决梯度消失的问题，即无法学习出在较早的时间步骤的网络层的参数，将会导致RNN结构只具有短期记忆！

5. LSTM 与 GRU

  为了解决传统的RNN，仅仅具有短期记忆的不足，两种特别的循环神经网络被创造出来，解决这个问题。一种被称为 Long Short-Term Memory(简称LSTM)，另一种被称为 Gated Recurrent Units(简称GRU)。

  LSTM和GRU的基本功能与RNN一样，但它们能够使用称为 门 (gate) 的机制学习长期依赖关系。这些 门 是不同的张量操作，用来学习我们应该向隐藏状态中添加或删除什么信息。由于这种能力，短期记忆对他们来说就不那么大的问题了。

  下面我将详细阐述这两种神经网络的结构。

5.1 短期记忆的问题

  前面提到过，循环神经网络存在的最大问题，就是只能将序列数据编码之后，只能保留短期记忆。那么如果一个序列数据足够的长，它将很难把序列早期数据所携带的信息，传给序列后期的数据。所以如果你准备处理一段文本信息，并进行预测任务的话，RNN很有可能会遗漏掉文本开头所携带的重要信息。

  造成短期记忆的主要原因，是因为神经网络训练时用到的反向传播算法，然后带来的其固有的梯度消失问题，如果上一层中，传来的梯度值很小的话，本轮的权重值，几乎没怎么更新，如下图所示：

5.2 LSTM 和 GRU 的解决方案

  LSTM 和 GRU 都是用来解决短期记忆问题的循环神经网络，它们在内部都有一种被称为门的机制，用来调节信息流。如下图所示：

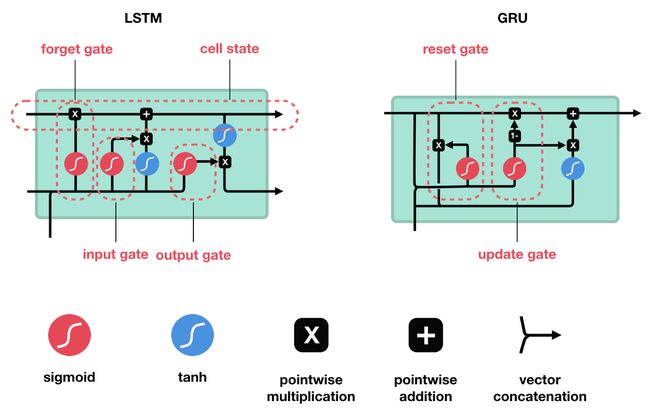
  这些门，可以学习出序列数据中的每个数据的重要性，从而决定是将其保留还是舍弃。 通过这个做法，它可以将相关信息传递到长序列中，从而作出预测。几乎目前所有的基于循环神经网络的技术成果，都是通过这两种网络实现的。

  LSTM和GRU在语音识别、语音合成和文本生成方面都有研究。你甚至可以用这两种循环神经网络为视频生成标题。

  这里呢，主要是想告诉你LSTM、GRU与传统RNN相比，主要做了哪些结构上的改变，接下来我们将从直观的角度，来理解它们为什么可以解决短期记忆的问题。

5.3 直觉

  我们继续和前面一样，发挥一下想象力，进行一个思想实验！

  首先，假设你在网上阅读某件商品的评价，根据这个评价，来分析该买家对这件商品的评价是好还是坏，具体如下：

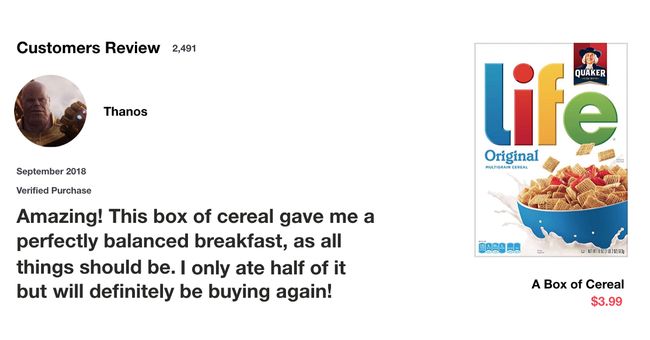
  当你阅读这个评价时，我想你的大脑，会在潜意识里仅仅记住几个关键词，如 $Amazing$、$perfectlybalancedbreakfast$这些词语。而相比之下，对于$This、gave、all、should$等词，你可能就没有太在意。

  等到第二天，你的朋友问你这件商品的评价时，你很有可能已经记不太清这条评价到底说了啥，可能只对 $willdefinitelybebuyingagain$像这样的中心意思比较有印象。

  实际上，这个就是 LSTM 或者 GRU 所做的事情！ 它们能学习出，仅仅保留与预测结果相关性较高的信息，然后舍弃掉那些相关性较低的数据，最终你的预测结果是 $Thisproductisgood.$

5.4 回顾一下循环神经网络

  为了搞清楚 LSTM 和 GRU 是怎么实现上面这个功能的，我们先来回顾一下一个普通的循环神经网络是如何工作的。

  它主要分成两个过程，一是文本转成向量的形式；二是将这些有序的向量，逐个的送给RNN模型进行编码。 大致过程如下：

  当它每一次处理信息时，都会把前面所更新的 hidden state 作为输入传进来，它把当前时间步骤之前输入的数据信息全都保留了下来。

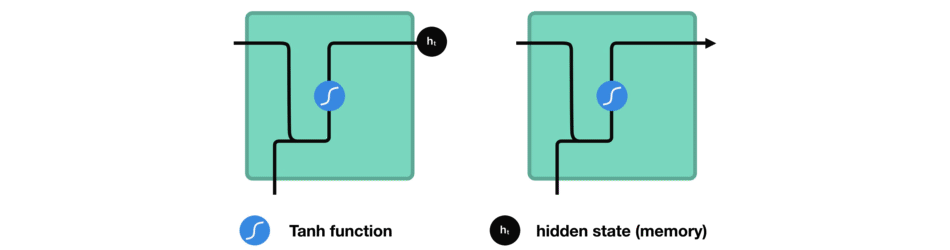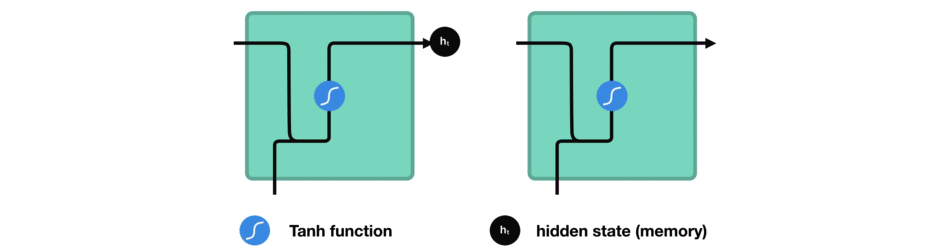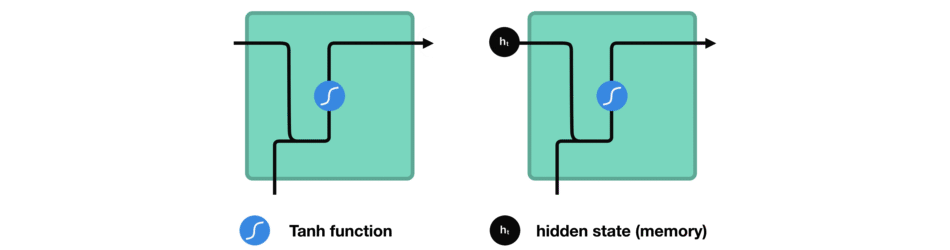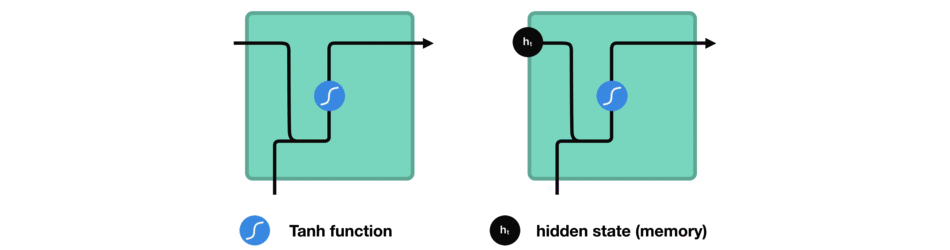
  我们来观察一下RNN中的某个神经单元，看看它是如何计算隐藏状态的。首先，我们将本轮的输入和先前的隐藏状态组合成一个向量。那么该向量现在有当前输入和先前输入的信息。该向量经过tanh函数激活之后，输出即是新的隐藏状态。

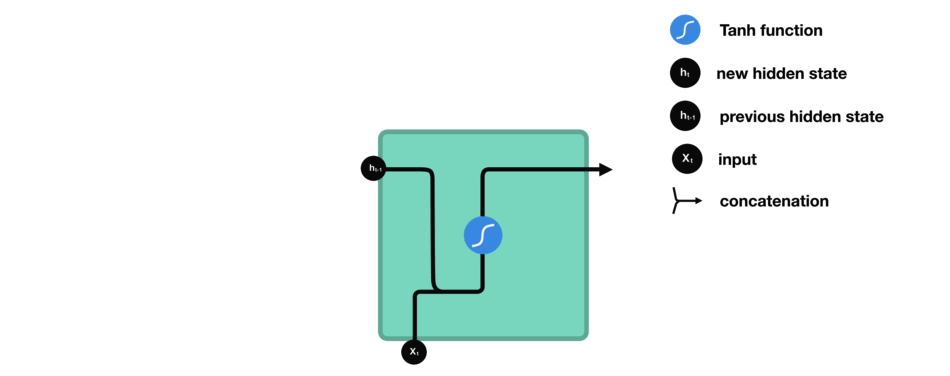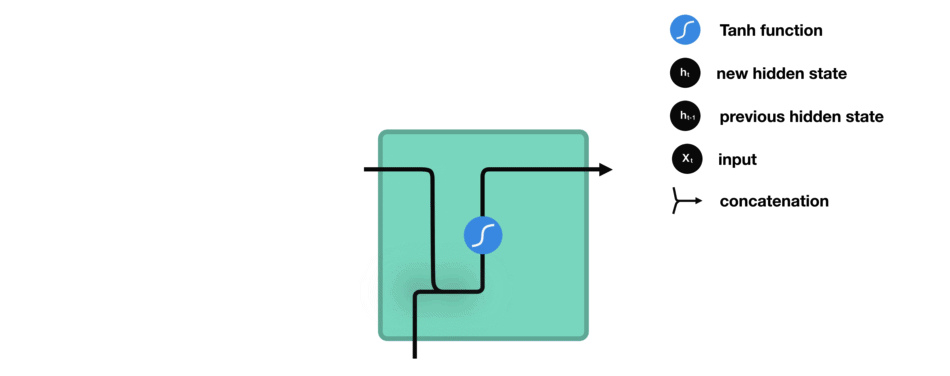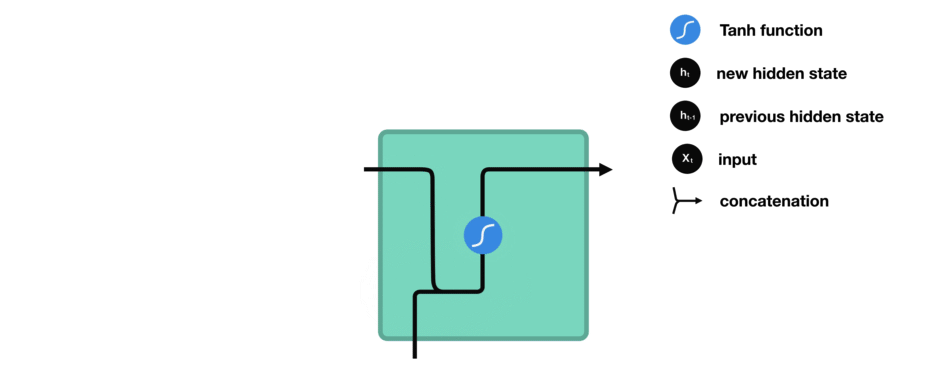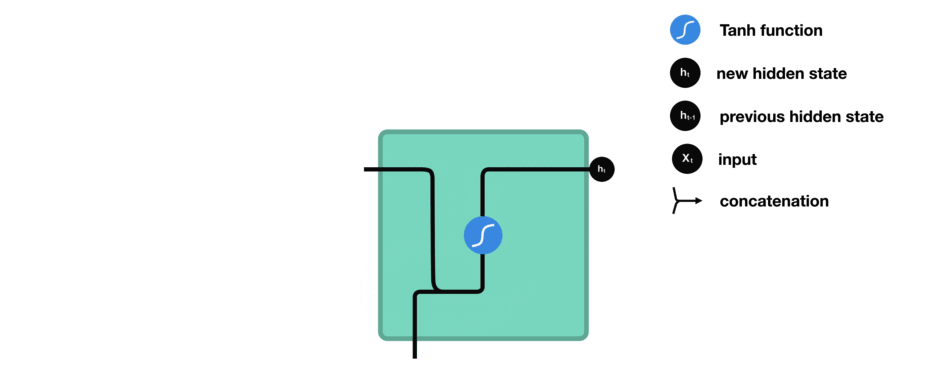
5.5 Tanh 激活函数

   Tanh激活函数用于调节流经网络的值，将这些值压缩到 -1 和 1 之间。

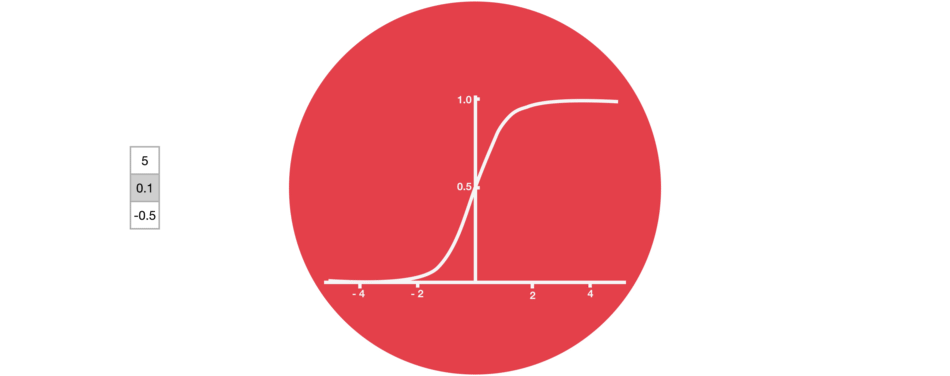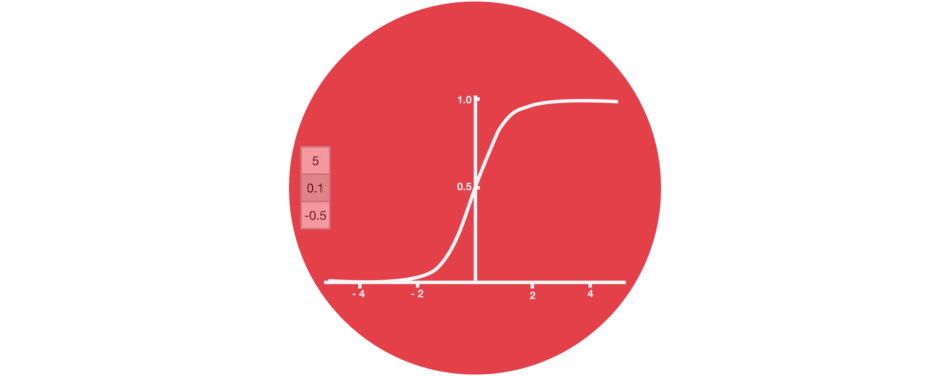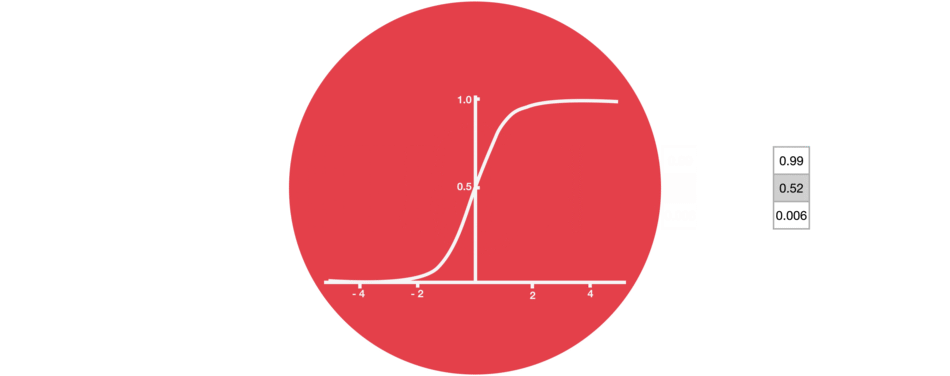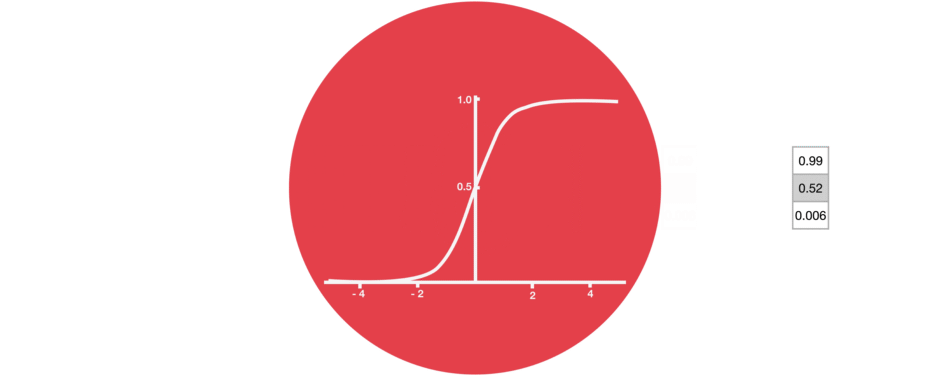
  当某个向量流经神经网络时，由于各种数学运算，它会经历许多次变换。假设一个值连续乘以3，并且变换次数足够的多，你将会发现这个值最终变成特别大的数字，导致向量中的其他值，显得微不足道！

  如下图所示，向量中的第一个元素5，最终变成了405，而向量中的其他元素，则显得微乎其微。

  那么在神经元的运算中，引入 Tanh 函数的作用就很明显了，它能保证网络中每一个节点的输出，都能处于$[-1,1]$的范围内，在上面的神经元中，引入一个 Tanh 函数，我们观察最终输出的差别。

  那么以上，就是一个经典的RNN的结构图。 它在处理短序列的数据问题中，预测效果是非常好的，并且相比于 LSTM 和 GRU ，它占用的计算资源要小的多。

5.6 LSTM

  LSTM具有与循环神经网络相似的控制流程，即它也是在向前传播时处理用于传递信息的数据， 主要差别在于是LSTM单元内的操作：

  上图出现的这些函数，使得 LSTM 能够存储或者舍弃传递的信息，我们接下来逐个解释这些函数的作用。

5.6.1 LSTM的核心概念

  LSTM的核心概念就是 Cell state (单元状态或者细胞状态），它有着各种各样的门。（Cell state 所在的区域，参考5.2节中的示意图）

  细胞状态充当着一条传输通道，用于在整个序列链中传输相关性信息，你可以把它看作是网络的“记忆”。

  理论上，细胞状态可以在整个序列数据处理过程中携带其相关性信息。因此，即使是来自早期时间步骤的信息也可以使其成为后期时间步骤的方法，从而减少短期记忆的影响。

  随着细胞状态的变化，信息可以通过细胞里的门，被添加或删除到细胞状态中。这些门是不同的神经网络，决定在细胞状态哪些信息是被允许通过的。在训练过程中，这些门可以学习出哪些信息是相关的，哪些信息是需要保留或舍弃的。

5.6.2 Sigmoid函数

  Sigmoid 激活函数和前面提到的 Tanh 激活函数是相似的，只不过它不是把值压缩到$[-1,1]$，而是压缩到$[0,1]$区间。这个性质有助于我们遗忘和更新序列数据，因为任何一个数乘以0都还是0，也就意味着这个值被遗忘了；任何一个数乘以1还是它本身，意味着这个被保留了下来。

  由于上述的 Sigmoid 函数的映射特点，它才可以成为 LSTM 或 GRU 神经单元中 门 的核心函数，请对此一定要留下深刻的印象，后面再在 门 的设计中具体感受！

  那我们接下来重点聊一聊LSTM结构中，设计的几个门吧，分别是 forget gate, input gate和 output gate。（忘记了这三个门在神经单元中的位置的同学，请翻到文章上面 5.2节进行回顾）

5.6.3 Forget gate

  从名字就可以看出来，Forget gate 中文名为遗忘门，这个门用来决定信息是应该被保留还是被丢掉。将先前隐藏状态的信息和来自当前输入的信息组合成一个向量，通过 Sigmoid 函数激活，激活值在0和1之间。越接近0越意味着忘记，越接近1越意味着保留。

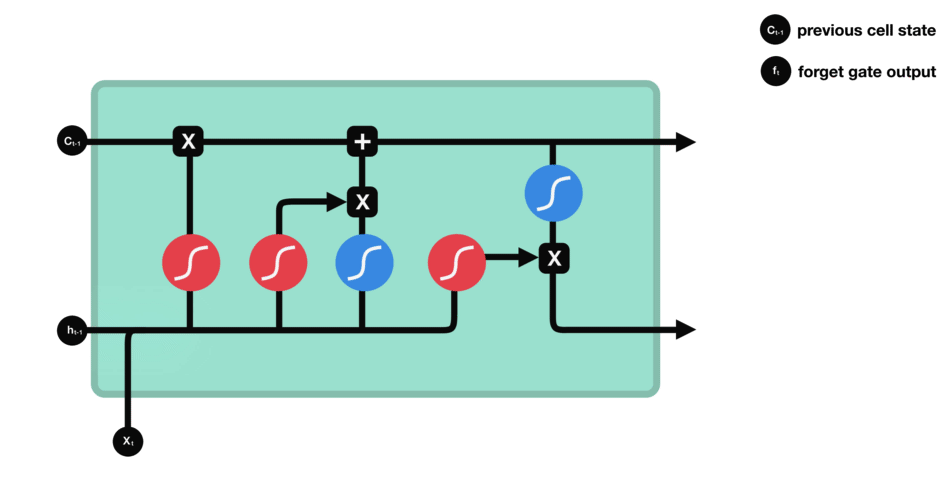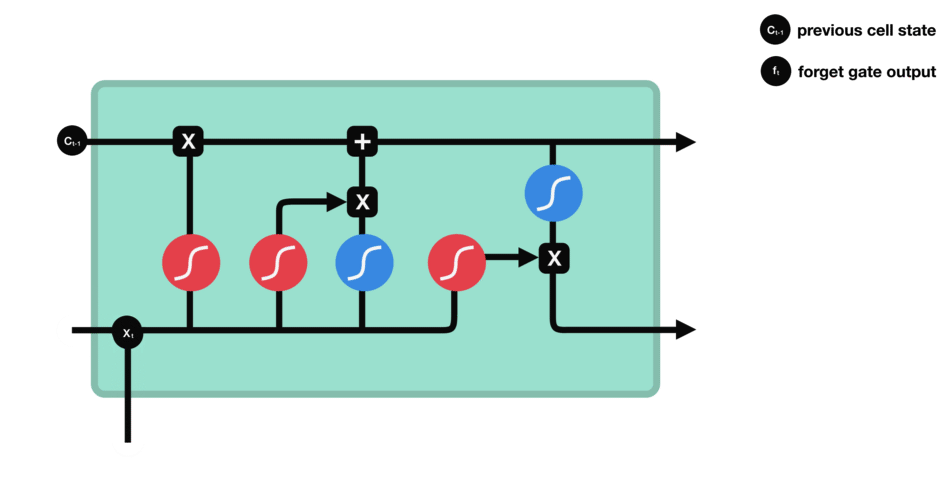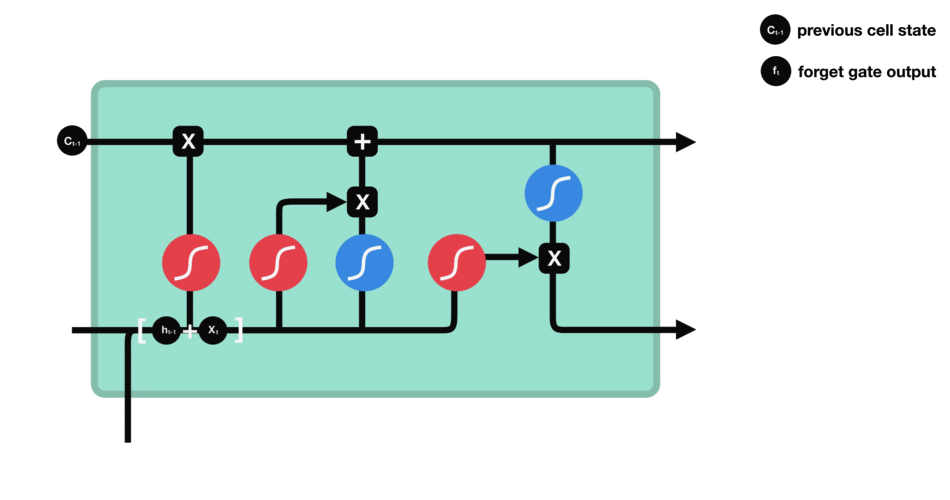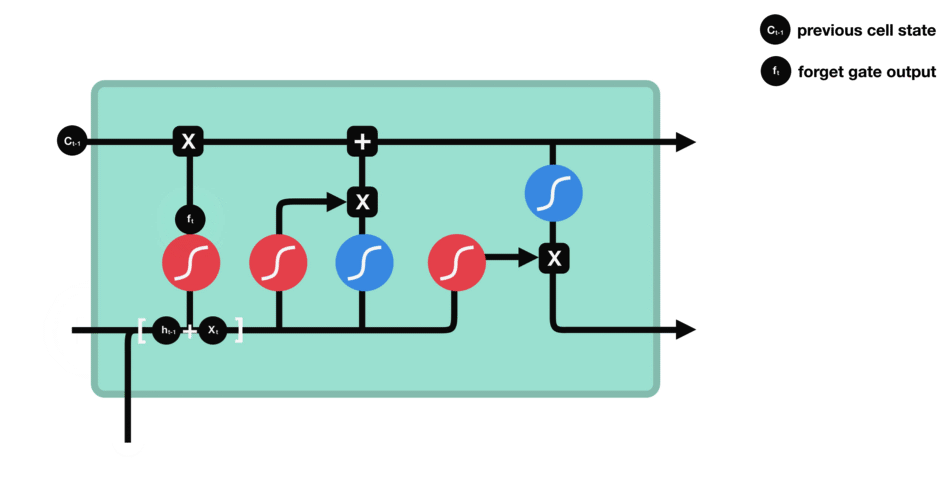
  在LSTM的单元中，最左边的Sigmoid激活函数，充当着 遗忘门 的作用！

  注意，在 t 时刻，当前输入的序列数据用$X_t$表示，传进来的上一个时刻得到的隐藏状态信息用$h_{t-1}$表示，Forget gate 的输出用 $f_t$ 表示，上一个时刻的细胞状态所携带的信息用 $C_{t-1}$表示！

5.6.4 Input gate

  为了更新在 t 时刻的细胞状态，我们还需要有一个输入门。首先呢，我们将上一步的隐藏状态信息和当前输入组合成一个向量，传递到左边第二个 Sigmoid 函数中，输出的向量用 $i_t$ 表示。它通过将值转换为介于0和1之间来决定要更新哪些值，0表示不重要，1表示重要。

  另外，您还需要将上一步的隐藏状态信息和当前输入传递到 tanh 激活函数中，将输入值压缩到$[-1,1]$区间，以帮助调节网络的参数。

  最后再将 tanh 的输出与 Sigmoid 的输出的对应元素相乘。（Sigmoid函数的输出，用来决定 Tanh 输出的哪些信息是重要的~）

5.6.5 Cell state

  在有了 遗忘门 和 输入门 的输出之后，我们可以计算出 cell state 的值了。

  $step1:$ 我们把上一个时刻的细胞状态向量 $C_{t-1}$ 与 遗忘门 的输出 $f_t$ 向量的对应元素相乘，得到一个新的向量 $ve{c}_1$；

  $step2:$ 将输入门 的输出的 $f_t$ 向量与 tanh 的输出向量的对应元素相乘，得到一个新的向量 $ve{c}_2$；

  $step3:$ 将向量 $ve{c}_1$ 和 向量 $ve{c}_2$ 的对应位置的元素相加，即得到 当前时刻 t 下的 cell state，即 $C_t$;

5.6.6 Output gate

  输出门的输出值，即为下一个时间状态 (t+1)下 的 hidden state，用符号 $h_t$ 来表示。你应该还记得， hidden state 的作用是保留早先输入的所有信息。

  计算向量 $h_t$ 的值，需要以下几个步骤。

  $step1:$ 把向量 $h_{t-1}$ 和当前输入的序列数据 $x_t$ 组合成一个向量，喂给输出门的 Sigmoid 激活函数，得到一个新的向量 $ve{c}_3$；

  $step2:$ 把前面计算出来的时刻 t 下的 cell state 向量 $C_t$ 喂给 tanh 激活函数， 得到一个新的向量 $ve{c}_4$；

  $step3:$ 把上面两步得到的向量 $ve{c}_3$ 和 向量 $ve{c}_4$ 中的对应位置元素相乘，得到一个最终的向量 $h_t$，即为我们在 t 时刻的 hidden state 信息 ;

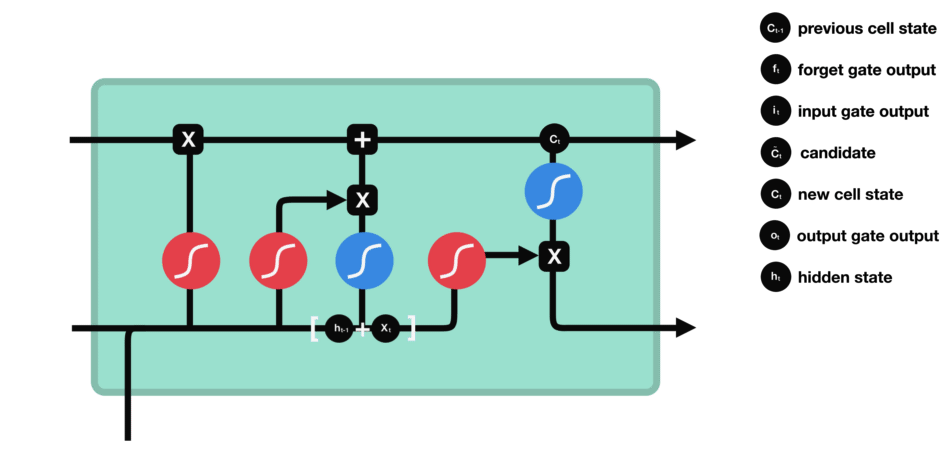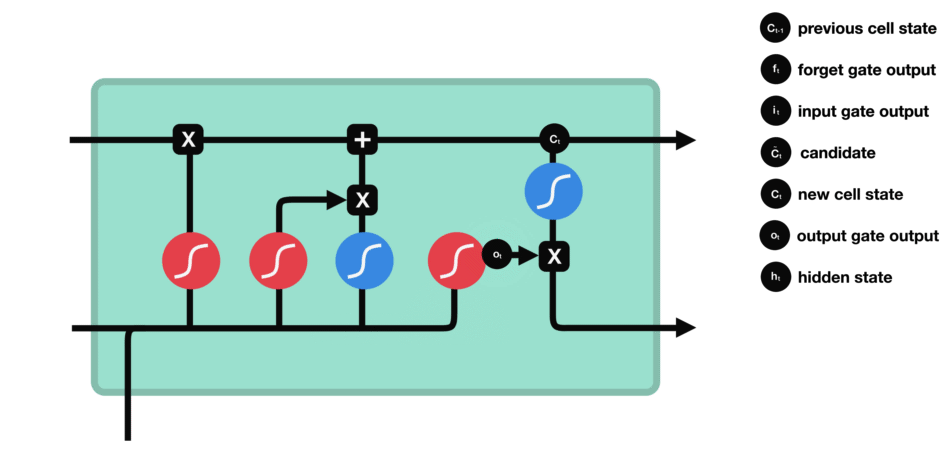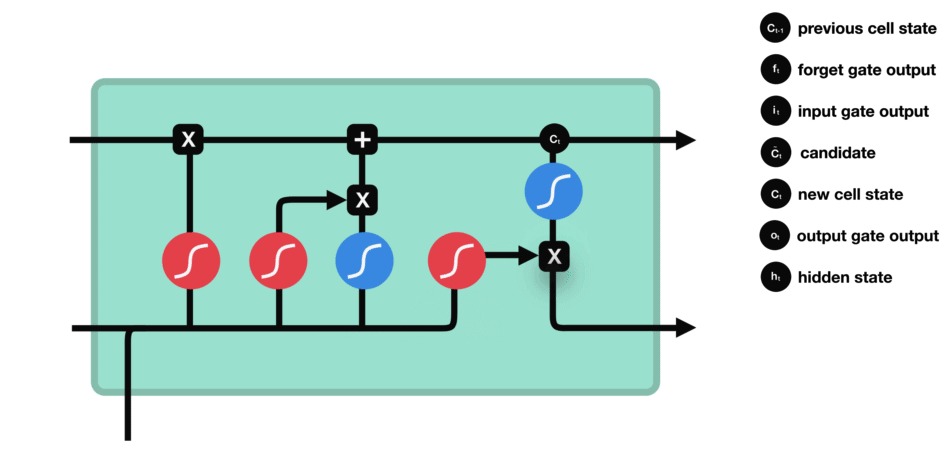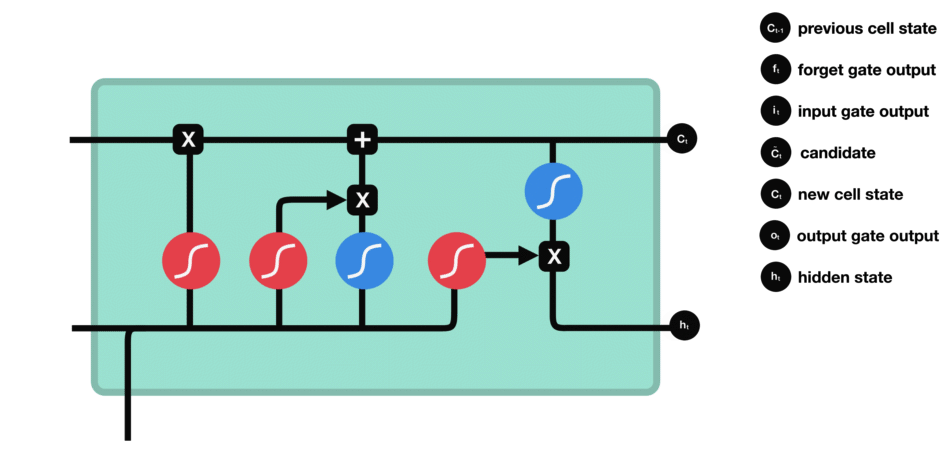
我们最后针对LSTM的几种门结构，做一个简短的总结：

1. Forget gate 的作用是决定与之前的步骤的数据保持相关性的信息；
2. Input gate 的作用是决定当前输入的序列数据中的哪些信息需要被添加进来；
3. Output gate 的作用是用来决定下一个隐藏状态应该是怎样的。

5.6.7 代码角度

  我们都知道，$Talkischeap,showmeyourcode.$ 咱们仍然可以把上面神经元里面的整个过程，从代码的角度进行理解，这样更容易明白信息流在 LSTM Cell 中具体的流动过程！

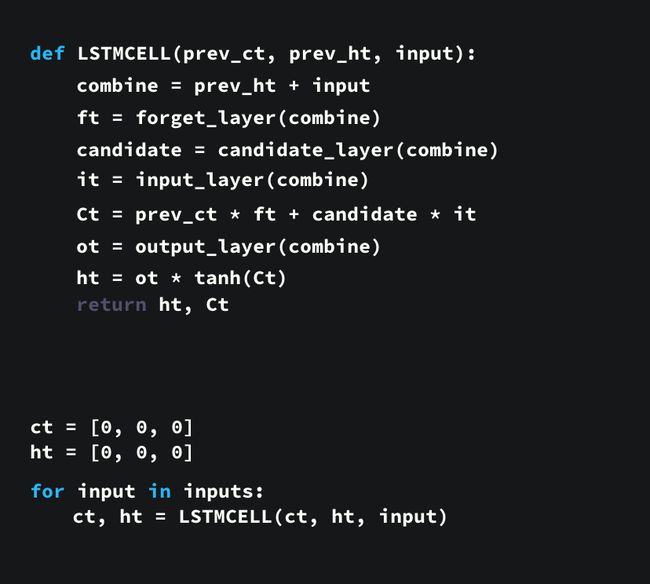
  对上述代码逐行进行解释。

1. 首先，我们把上一步得到的 hidden_state 向量和 当前序列数据的输入 input 向量组合成一个向量，命名为 combine 向量；
2. 把 combine 向量喂给 Forget_gate，即这里的 forget_layer()，Forget_gate 输出的向量用 ft 表示；
3. 把 combine 向量分别喂给 candidate() 和 input_layer()，输出的向量分别为 candadate 和 it；
4. 更新当前时刻 t 下的 cell_state，状态信息保存在 ct 向量中;
5. 把 combine 向量喂给 Output_gate，即这里的 output_layer()，Output_gate 输出的向量用 ot 表示；
6. 把前面得到的 ct 向量，喂给 tanh 激活函数，激活后的向量再与 ot 向量进行 Hadamard Product（对应位置元素相乘），最终得到当前时刻 t 下的 hidden_state 向量 ht；
7. 重复上面过程，把每一轮更新完的 ct 向量和 ht 向量，传递给 (t+1) 时刻的神经元进行训练，直至所有序列数据都编码完毕；

  就是这样！LSTM网络的控制流其实就是一些张量(tensor)运算和 for 循环。你可以使用这些 hidden state （隐藏状态信息）进行预测。结合所有的这些机制， LSTM 可以序列处理过程中选择哪些信息需要记忆、哪些信息需要遗忘！

5.7 GRU

  学习完 LSTM 的内部机制之后，咱们接下来简单看一看 GRU 的内部是如何设计的。GRU 是新一代的循环神经网络，并且它与 LSTM 十分相似，但是它更容易计算，对计算资源的要求相对低一些！

  主要的不同是，GRU 神经元中，去掉了 cell_state 这个状态信息，只用 hidden_state 来传递信息。它的内部机制中，只设置了两个门，分别是 reset gate 和 update gate.

  为了后面方便说明，我们对上图中流动的信息给出命名规则如下：

1. 左上方输入是上一步得到的 hidden state ，即 $h_{t-1}$ 向量；
2. 左下方输入是本轮序列数据的输入向量 $x_t$；
3. 右上方输出是本轮结束后得到的 hidden state 即 $h_t$ 向量；
4. reset gate 中有一个 Sigmoid 激活函数，它的输出值为 $r_t$ 向量；
5. update gate 中也有一个 Sigmoid 激活函数，它的输出值为 $z_t$ 向量；
6. 图中右侧还有一个 tanh 激活函数，它的输出值为 ${\tilde{y}}_t$ 向量；

5.7.1 reset gate

  我们来看看 重置门 做了哪些事情。

  $step1:$ 把 $h_{t-1}$ 向量与本轮的输入 $x_t$ 向量联合起来，组成一个新的向量，然后喂给 Sigmoid 函数激活，得到一个新的向量 $r_t$，即 $r_t=\sigma \left(W_r\cdot \left[h_{t-1},x_t\right]\right)$；

  $step2:$ 把生成的 $r_t$ 向量与输入的 $h_{t-1}$ 进行 Hadamard Product 运算，得到一个新的向量 $ve{c}_1$，其中 $ve{c}_1=r_t\odot h^{t-1}$；

  我们不难发现，重置门 的作用是来决定上一步中传进来的 hidden state 向量中，哪些元素需要保留下来，哪些元素需要舍弃！ 即它的核心是调整$h_{t-1}$向量中元素的重要程度。

5.7.2 update gate

   我们接下来再来看看 更新门 中具体做了哪些事情。

  $step1:$ 把 $h_{t-1}$ 向量与本轮的输入 $x_t$ 向量联合起来，组成一个新的向量，然后喂给 Sigmoid 函数激活，得到一个新的向量 $z_t$，即 $z_t=\sigma \left(W_z\cdot \left[h_{t-1},x_t\right]\right)$；

  $step2:$ 用一个元素全为1的向量，减去上面得到的 $z_t$ 向量，生成一个新向量 $ve{c}_2$，即 $ve{c}_2=1-z_t$；

  $step3:$ 将 $ve{c}_2$ 与 $h_{t-1}$ 进行 Hadamard Product 运算，得到一个新的向量 $ve{c}_3$，即 $ve{c}_3=ve{c}_2\odot h_{t-1}$；

5.7.3 hidden state

   我们再来看看，在 t 时刻，最终输出的 $h_t$ 是如何计算的。

  $step1:$ 在 reset gate 中，咱们最终得到了向量 $ve{c}_1$ (其中$ve{c}_1=r_t\odot h^{t-1}$)，我们再将 $ve{c}_1$ 与 $x_t$ 组合成一个新的向量 $ve{c}_4$，即 $ve{c}_4=[ve{c}_1,x_t]$；

  $step2:$ 把向量 $ve{c}_4$ 喂给 tanh 函数，输出向量为 ${\tilde{y}}_t$，即 ${\tilde{y}}_t=\tanh \left(W_{\tilde{h}}\cdot \left[r_t\ast h_{t-1},x_t\right]\right)$；

  $step3:$ 将 update gate 中 生成的 $z_t$ 向量与 ${\tilde{y}}_t$ 向量进行 Hadamard Product 运算，得到一个新的向量 $ve{c}_5$，即 $ve{c}_5=z_t\odot {\tilde{y}}_t$；

  $step4:$ 再把之前计算过的 $ve{c}_3$ 与 $ve{c}_5$ 的对应位置元素值相加，即得到我们最终的 hidden state 向量，即 $h_t=\left(1-z_t\right)\odot h_{t-1}+z_t\odot {\tilde{h}}_t$ 。

  那么以上就是 GRU 的内部机制！相比于 LSTM 神经元，GRU 设计到的张量(tensor)运算相对较少，因而运算速度更快一些。我们很难说这两种循环神经网络哪个更好，还是以具体应用为主进行比较！

Reference

  真心佩服国外大佬讲解问题的方式，请允许我先奉献出自己的膝盖 ~

1. Illustrated Guide to Recurrent Neural Networks
2. Illustrated Guide to LSTM’s and GRU’s: A step by step explanation