《深入浅出图神经网络》读书笔记（8. 图分类）

8. 图分类

对于非规则结构的图数据，之前的固定大小滑窗形式的池化操作不再适用，在图分类中实现层次化池化的机制，是GNN需要解决的基础问题。

8.1 基于全局池化的图分类

读出机制对经过K轮迭代的所有节点进行一次性聚合操作，从而输出图的全局表示：
$$y=R({h\text{h}h}_i^{(k)}|\forall v_i\in V)$$
读出机制可以使用MAX、SUM等函数；

还有一种做法是引入一个与所有节点相连的虚拟节点，将全图的表示等价于这个虚拟节点的表示。

注意：损失结构信息；适合小图数据。

8.2 基于层次化池化的图分类

三种方案：

1. 基于图坍缩的池化机制：将图划分为不同的子图，然后将子图视为超级节点，从而形成一个坍缩的图。
2. 基于TopK的池化机制：对图中的每个节点学习出一个分数，基于这个分数的排序丢弃一些低分数的节点，这类方法借鉴了CNN最大池化的思想：将更重要的信息筛选出来。不同的是图数据种难以实现局部滑窗操作，因此使用分数筛选；
3. 基于边收缩的池化机制：边收缩是指并行地将图中的边移除，并将被移除边的两个节点合并，保持它们的连接关系，其思路是通过归并操作来逐步学习图的全局信息的方法。

8.2.1 基于图坍缩的池化机制

1.图坍缩

图G，某种划分得到K个子图$\{G^{(k)}{\}}_{k=1}^K$,${\Gamma }^{(k)}$表示子图$G^{(k)}$中的节点列表。

簇分配矩阵$S\in R^{N\times K}$，其定义如下：$S_{ij}=1$当且仅当$v_i\in {\Gamma }^{(j)}$.

$S^{T}AS$的意义：第i个簇与第j个簇的连接强度。
$$A_{\text{coar}}=S^{T}AS$$
表述了图坍缩之后的超级节点之间的连接强度，其中包含了超级节点自身内部的连接强度，如果只需要考虑超级节点之间的连接强度$A_{\text{coar}}[i,i]=0$。

采样算子$C\in R^{N\times N_k}$,其定义为：$C_{ij}^{(k)}=1$,当且仅当${\Gamma }_j^{(k)}=v_i$.

C是节点在原图和子图中顺序关系的一个指示矩阵。

下采样：
$${x\text{x}x}^{(k)}=(C^{(k)}{)}^{T}x\text{x}x$$
上采样：
$$\overline{x\text{x}x}=C^{(k)}x\text{x}x$$
邻接矩阵A的划分使用采样算子：
$$A^{(k)}=(C^{(k)}{)}^{T}A{C}^{(k)}$$
这样就可以计算簇内之间的连接关系。

确定簇内节点的融合方法，可以将结果表示为超级节点上的信号。迭代重复上述过程，就能获得越来越全局的图信号。一个实例如下：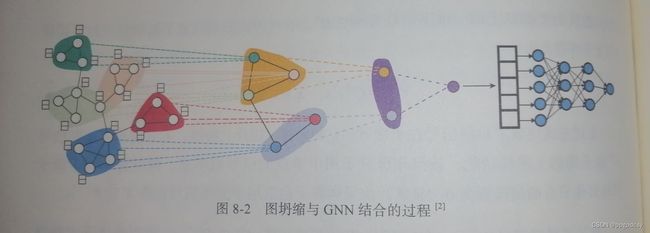

2.DIFFPOOL

首个将图坍缩与GNN结合起来的图层面任务学习的算法。DIFFPOOL提出了一个可学习的簇分配矩阵。具体来说，首先通过一个GNN对每个节点进行特征学习，然后通过另一个GNN为每个节点学习出所属各个簇的概率分布：
$$\begin{gathered} Z^{(l)}=GN{N}_{l,embed}(A^{(l)},H^{(l)}) \\ {S}^{(l)}=\text{softmax}(GN{N}_{l,pool}(A^{(l)},H^{(l)})) \\ {H}^{(l+1)}={S^{(l)}}^T{Z}^{(l)} \\ {A}^{(l+1)}={S^{(l)}}^{T}A{S}^{(l)} \end{gathered}$$
后两个公式被称为DIFFPOOL层，前一个是融合，明显是加和节点特征，后一个是簇间邻接矩阵的计算。

前两个式子是通过GNN学习得到的，学习目的不同，参数不同。

DIFFPOOL有一个非常重要的特性：排列不变性。GCN也是具有排列不变性的，因此上述使用GNN若是GCN，那么节点是否重新排列并不影响节点聚合成簇的结果。

3.EigenPooling

图坍缩使用谱聚类算法来进行划分，基本思路是先将数据变换到特征空间以凸显更好的区分度，然后执行聚类操作（比如选择Kmeans算法进行聚类，此时簇分配就是一种硬分配，保证了稀疏性）。

池化操作选用频谱信息来表示子图信息的统一整合：

假设子图$G^{(k)}$的拉普拉斯矩阵为$L^{(k)}$，对应特征向量${u\text{u}u}_1^{(k)},{u\text{u}u}_2^{(k)},...,{u\text{u}u}_{N_k}^{(k)}$，可以使用上采样算子$C^{(k)}$将该特征向量（子图上的傅里叶基）上采样到整个图：
$${\overline{u\text{u}u}}_l^{(k)}=C^{(k)}{u\text{u}u}_l^{(k)}$$
池化算子${\Theta }_l\in R^{N\times K}$，我们将所有子图的第$l$个特征向量按行方向组织起来形成矩阵${\Theta }_l$，即：
$${\Theta }_l=[{u\text{u}u}_l^{(1)},...,{u\text{u}u}_l^{(k)}]$$
由于子图的节点数量不同，因此特征向量的数量也不同。用$N_{max}={\max }_{k=1,...,K}{N}_k$表示子图中的最大节点数。然后，若子图$G^{(k)}$的节点数小于$N_{max}$，可以将${u\text{u}u}_l^{(k)}(N_k<l<N_{max})$设置为$0\text{0}0\in R^{N_k\times 1}$.

池化过程如下：
$$X_l={\Theta }_l^{T}X$$
$X_l$在每个子图第$l$个特征向量作用下得到的,$X_l$的第k行表示的是第k个超级节点在${\Theta }_l$的作用下的表示向量。按照该机制，我们需要设计$N_{max}$个池化算子进行同样的操作，再进行列方向拼接，结果如下：
$$X_{pooled}=[X_0,...,X_{N_{max}}]$$
具体实例可见下图：

由于低频信息的有效性，取$H<<N_{\max }$
$$X_{\text{coar}}=X_{pooked}=[X_0,...,X_H]$$
设全图上的信号为$x\text{x}x$，有
$$({\overline{u\text{u}u}}_l^{(k)}{)}^{T}x\text{x}x=({u\text{u}u}_l^{(k)}{)}^T(C^{(k)}{)}^{T}x\text{x}x=({u\text{u}u}_l^{(k)}{)}^T{x\text{x}x}^{(k)}$$
其输出表示子图上的信号在子图上对应的第$l$个特征向量上的傅里叶系数。

8.2.2 基于TopK的池化机制

这是一个不断丢弃节点的过程。具体来说，首先设置一个表示池化率的超参数$k$,$k\in (0,1)$,接着学习出一个表示节点重要度的值z并并对其进行降序排序，将全图$N$个节点下采样到$kN$​个节点。
$$\begin{gathered} i\text{i}i=\text{top}-\text{rank}(z\text{z}z,kN) \\ {X}^{{}^{\prime }}=X_{i,:} \\ {A}^{{}^{\prime }}=A_{i,i} \end{gathered}$$
$X_{i,:}$表示按照向量i的值对特征矩阵进行行切片，$A_{i,i}$表示按照向量$i\text{i}i$的值对邻接矩阵同时进行行切片和列切片。DIFFPOOL分配同样的问题需要$k{N}^2$的空间复杂度来分配簇信息，而基于Topk的池化机制，每次只需要从原图中丢弃$(1-k)N$的节点即可。

节点重要度的计算：

a.为图分类模型设置一个全局的基向量$p\text{p}p$,将节点特征向量在该基向量上的投影当作重要度：
$$z\text{z}z=\frac{X_{p\text{p}p}}{||p\text{p}p||}$$
两个作用：

1. 可以以投影大小来确定Topk的排序；
2. 投影大小还起到了一个梯度门限的作用，投影较小的节点仅有较小的梯度更新幅度，相对地，投影较大的节点会获得更加充分的梯度信息。

$$\begin{gathered} z\text{z}z=\frac{X_{p\text{p}p}}{||p\text{p}p||},i\text{i}i=\text{top}-\text{rank}(z\text{z}z,kN) \\ {X}^{{}^{\prime }}={(X\odot \text{tanh}(z\text{z}z))}_{i,:} \\ {A}^{{}^{\prime }}=A_{i,i} \end{gathered}$$

点乘是利用节点的重要度对节点特征做了一次收缩变换，进一步强化了对重要度高的节点的梯度学习。——gpool层。

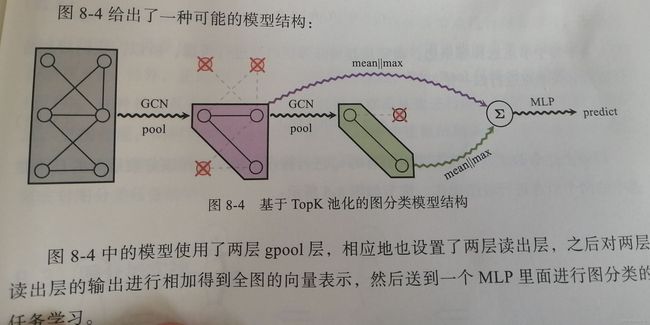
但是上述做法缺乏对所有节点的有效信息的融合，因此在gpool层后跟一个读出层，实现该尺度下的图全局信息的一次性聚合。具体实现是将全局平均池化和全局最大池化拼接起来：
$$s\text{s}s=\frac{1}{N}\sum _{i=1}^N{x\text{x}x}_i^{{}^{\prime }}||\underset{i=1}{\overset{N}{\max }}{x\text{x}x}_i^{{}^{\prime }}$$
全图表示，将各层s相加：
$$s\text{s}s=\sum _{l=1}^L{s\text{s}s}^{(l)}$$

b.使用一个GNN对节点重要度进行学习，这样能更好地利用图的结构信息对节点的重要度进行学习。

8.2.3 基于边收缩的池化机制

基本思想：迭代式地对每条边上的节点进行两两归并形成一个新的节点，同时保留合并前两个节点的连接关系到新节点上。

存在问题：每个节点有多条边，但是每个节点只能从属于一条边进行边收缩，如何选择？

EdgePool设计了一个边上的分数，根据该分数进行非重复式地挑选与合并。

过程如下：

计算每条边的原始分数：
$$r_{ij}={w\text{w}w}^T[{h\text{h}h}_i||{h\text{h}h}_j]+b$$
对原始分数沿邻居节点进行归一化：
$$s_{ij}={\text{softmax}}_j(r_{ij})$$
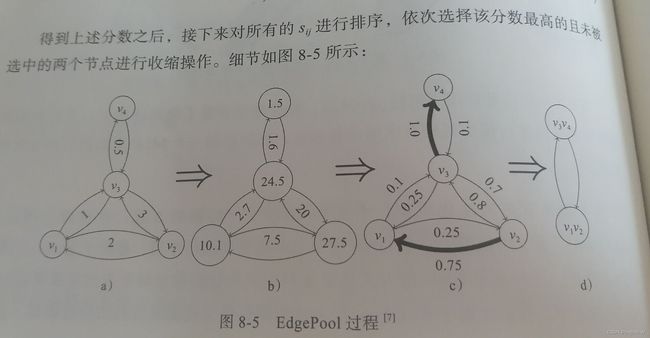
得到上述分数之后，接下来对所有的$s_{ij}$进行排序，依次选择该分数最高并且未被选中的两个节点进行收缩操作。细节如下：

a为原始分数，b为$e^r$，c为归一化之后的结果，先合并最高的$v_3,v_4$，再合并较高的$v_1,v_2$.

合并之后的节点特征可以使用求和的方式：
$${h\text{h}h}_{ij}=s({h\text{h}h}_i+{h\text{h}h}_j),s=\max (s_{ij},s_{ji})$$
s同样是收缩作用。

oe4-1669389714951)]

a为原始分数，b为$e^r$，c为归一化之后的结果，先合并最高的$v_3,v_4$，再合并较高的$v_1,v_2$.

合并之后的节点特征可以使用求和的方式：
$${h\text{h}h}_{ij}=s({h\text{h}h}_i+{h\text{h}h}_j),s=\max (s_{ij},s_{ji})$$
s同样是收缩作用。

这种方法节点的融合都是从边进行的，契合了图的结构信息；保留了融合之后图中连接的稀疏性，空间复杂度低；作为一种端到端的池化机制，可以广泛地整合到各个GNN模型中，以完成图分类任务的学习。