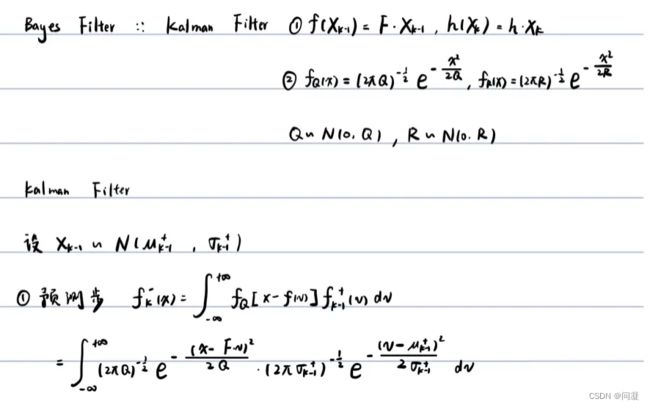【卡尔曼滤波的原理以及Matlab和python代码实现】

---

前言

本文主要讲解卡尔曼滤波的原理以及Matlab和python代码实现。

---

一、卡尔曼滤波原理

最后对卡尔曼滤波的预测步和更新步公式进行总结：

二、Matlab代码

%X(K)=F*X(K-1)+Q
%Y(K)=H*X(K)+R
%%%第一个问题，生成一段随机信号，并滤波

%生成一段时间t
t=0.1:0.01:1;
L=length(t);
%生成真实信号x，以及观测y
%首先初始化
x=zeros(1,L);
y=x;
y2=x;
%生成信号，设x=t^2
for i=1:L
    x(i)=t(i)^2;
    y(i)=x(i)+normrnd(0,0.1);%正态分布，参数为期望和标准差
    y2(i)=x(i)+normrnd(0,0.1);
end

%观测方程好写Y(K)=X(K)+R R~N(0,1)
%模型一，最粗糙的建模
%X(K)=X(K-1)+Q
%Y(K)=X(K)+R
%猜Q~N(0,1);
F1=1;
H1=1;
Q1=1;
R1=1;
%初始化x(k)+
Xplus1=zeros(1,L);%plus + 的英语 minus -的英语
%我们会经常用到Xplus,Xminus,Pplus,Pminus
%设置一个初值，假设Xplus1(1)~N(0.01,0.01^2)
Xplus1(1)=0.01;
Pplus1=0.01^2;
%%%卡尔曼滤波算法
%X(K)minus=F*X(K-1)plus
%P(K)minus=F*P(K-1)plus*F'+Q
%K=P(K)minus*H'*inv(H*P(K)minus*H'+R)
%X(K)plus=X(K)minus+K*(y(k)-H*X(K)minus)
%P(K)plus=(I-K*H)*P(K)minus
for i=2:L
    %%%%预测步%%%%%%
    Xminus1=F1*Xplus1(i-1);
    Pminus1=F1*Pplus1*F1'+Q1;
    %%%%%更新步%%%%%
    K1=(Pminus1*H1')*inv(H1*Pminus1*H1'+R1);
    Xplus1(i)=Xminus1+K1*(y(i)-H1*Xminus1);
    Pplus1=(1-K1*H1)*Pminus1;
end
%模型2
%X(K)=X(K-1)+X'(K-1)*dt+X''(K-1)*dt^2*(1/2!)+Q2
%Y(K)=X(K)+R R~N(0,1)
%此时状态变量X=[X(K)    X'(K)    X''(K) ]T(列向量）
%Y(K)=H*X+R    H=[1   0   0](行向量）
%预测方程
%X(K)=X(K-1)+X'(K-1)*dt+X''(K-1)*dt^2*(1/2!)+Q2
%X'(K)=0*X(K-1)+X'(K-1)+X''(K-1)*dt+Q3
%X''(K)=0*X(K-1)+0*X'(K-1)+X''(K-1)+Q4  %%多项式信号多求几阶导数，总会比较平缓，而
%X''(K)=X''(K-1)+Q3正是描述平缓的随机过程，这种建模相对精细一些，适用范围也较广
%F= 1    dt     0.5*dt^2
%      0     1         dt
%      0      0         1
%H=[1     0     0]
%Q= Q2   0    0
%      0     Q3   0
%       0     0     Q4 协方差矩阵
dt=t(2)-t(1);
F2=[1,   dt,   0.5*dt^2;0,   1,   dt;0,   0,     1];%%%此处要注意矩阵是否病态，若dt特别小，易导致矩阵病态或精度丢失
H2=[1,0,0];
Q2=[1,  0,  0;0,  0.01,  0;0,  0,  0.0001];
R2=3;
%%%设置初值%%%%
Xplus2=zeros(3,L);
Xplus2(1,1)=0.1^2;
Xplus2(2,1)=0;
Xplus2(3,1)=0;
Pplus2=[0.01, 0,   0;0,    0.01,   0;0,   0,    0.0001];
for i=2:L
    %%%预测步%%%
    Xminus2=F2*Xplus2(:,i-1);
    Pminus2=F2*Pplus2*F2'+Q2;
    %%%更新步%%%%
    K2=(Pminus2*H2')*inv(H2*Pminus2*H2'+R2);
    Xplus2(:,i)=Xminus2+K2*(y(i)-H2*Xminus2);
    Pplus2=(eye(3)-K2*H2)*Pminus2;
end

%问题2，两个传感器，进行滤波
% Y1(K)=X(K)+R
% Y2(K)=X(K)+R
%H=[1 1]T (列向量) X=X(K)
%H=1   0     0     X=X(K)   X'(K)   X''(K)
%     1   0     0
F3=[1,   dt,   0.5*dt^2;0,   1,   dt;0,   0,     1];%%%此处要注意矩阵是否病态，若dt特别小，易导致矩阵病态或精度丢失
H3=[1,0,0;1,0,0];
Q3=[1,  0,  0;0,  0.01,  0;0,  0,  0.0001];
R3=[3,0;0,3];%%%%%一定要注意是协方差矩阵
Xplus3=zeros(3,L);
Xplus3(1,1)=0.1^2;
Xplus3(2,1)=0;
Xplus3(3,1)=0;
Pplus3=[0.01, 0,   0;0,    0.01,   0;0,   0,    0.0001];
for i=2:L
   %%%预测步%%%
    Xminus3=F3*Xplus3(:,i-1);
    Pminus3=F3*Pplus3*F3'+Q3;
    %%%更新步%%%%
    K3=(Pminus3*H3')*inv(H3*Pminus3*H3'+R3);
    Y=zeros(2,1);
    Y(1,1)= y(i);
    Y(2,1)=y2(i);
    Xplus3(:,i)=Xminus3+K3*(Y-H3*Xminus3);
    Pplus3=(eye(3)-K3*H3)*Pminus3;
end
plot(t,x,'r',t,y,'g',t,Xplus2(1,:),'k',t,Xplus3(1,:),'m','LineWidth',2); 

三、Python代码

import numpy as np
import matplotlib.pyplot as plt

t = []

for ele in range(10,100,1):
    t.append(0.01 * ele)

L = len(t)

x = np.zeros((1,L))

y = np.zeros((1,L))

for i in range(1,L):
    x[0,i] = t[i] * t[i]
    y[0,i] = x[0,i] + np.random.normal(0.0,0.1)

ylll = []
for ele in range(L):
    ylll.append(y[0,ele])

 模型1
 X(k) = X(k-1) + Q1
Y(k) = X(k) + R1   Q1为预测噪声,R1为观测噪声

F1 = 1
H1 = 1
Q1 = 0.1
R1 = 1
Xplus1 = np.zeros((1,L))

Xplus1[0,0] = 0.01
Yplus1 = 0.01 * 0.01

for j in range(1,L):
    Xminus1 = F1 * Xplus1[0,j-1]
    Yminus1 = F1 * Xminus1 * np.transpose(F1) + Q1

    K = Yminus1 * np.transpose(H1) / (H1*Yminus1*np.transpose(H1)+R1)#np.linalg.inv(H1*Yminus1*np.transpose(H1)+R1)
    Xplus1[0,j] = Xminus1 + K * (y[0,j] - H1 * Xminus1)
    Yplus1 = (np.eye(1) - K * H1) * Yminus1

xls = []
yls = []
Xplus1ls = []

for e in range(L):
    xls.append(x[0,e])
    yls.append(y[0,e])
    Xplus1ls.append(Xplus1[0,e])

模型2
X(k) = X(k-1) + X‘(k-1) * dt + 0.5 * X‘’(k-1) * (dt)^2+ Q2
 Y(k) = X(k) + R   Q2为预测噪声,R2为观测噪声
dt = 0.01
F2 = np.array([[1,dt,0.5*dt*dt],[0,1,dt],[0,0,1]])
H2 = np.array([[1,0,0]])
Q2 = np.array([[1,0,0],[0,0.01,0],[0,0,0.0001]])
R2 = 0.5

Xplus2 = np.zeros((3,L))
Xplus2[0,0] = 0.1 * 0.1
Xplus2[1,0] = 0
Xplus2[2,0] = 0
Yplus2 = np.array([[0.01,0,0],[0,0.01,0],[0,0,0.0001]])

for m in range(L):

    # 预测步
    Xminus2 = np.dot(F2,Xplus2[:,m])
    Yminus2 = np.dot(np.dot(F2,Yplus2),np.transpose(F2)) + Q2

    # 更新步
    K2 = np.dot(Yminus2,np.transpose(H2)) * np.linalg.inv(np.dot(np.dot(H2,Yminus2),np.transpose(H2)) + R2)
    Xplus2[:,m] = Xminus2 + np.dot(K2,ylll[m] - np.dot(H2,Xminus2))
    Yplus2 = np.dot(np.identity(3) - np.dot(K2,H2),Yminus2)

Xplus2ls = []
print(Xplus2)
print(np.identity(3))

for uu in range(L):
    Xplus2ls.append(Xplus2[0,uu])


plt.plot(t,xls,'k')  # xls为抛物线x^2的函数上一些点绘制的曲线
plt.plot(t,yls,'r')  # yls为在xls上添加服从均值为 0方差 0.1的一些正态分布的噪点绘制而成的曲线
plt.plot(t,Xplus1ls,'c') # Xplus1ls为用模型1卡尔曼滤波后得到的点绘制而成的曲线
plt.plot(t,Xplus2[0,:],'g') # Xplus2[0,:]为用模型2卡尔曼滤波后得到的点绘制而成的曲线
plt.show()

以上就是卡尔曼滤波的原理以及代码实现，变量的含义在代码的注释中写的很清楚，欢迎大家来一起学习卡尔曼滤波。