经纬度坐标转换为工程坐标

1. 绪论

在施工和工程测量时，经常需要将GPS坐标转换为工程中所使用的坐标。在Bing上检索到的类似问题，基本描述为两个坐标系的转换，但实际上并非如此。

本文将详细解释转换过程和转换方法。

1.1 GPS接收的坐标

GPS使用的坐标系称为大地坐标系。在GPS信号中，其所返回的经度、维度、和高程坐标一般分为以下几种：

1. WGS84坐标系：美国建立的世界大地坐标系(World Geodetic System, WGS)WGS-60、WGS-66、WGS-72，1984年修正完善为更精确的系统。
2. GCJ02坐标系：即火星坐标系，国测局坐标系。是由中国国家测绘局制定。由WGS84坐标系经加密后的坐标系。谷歌中国和搜搜中国采用的GCJ02地理坐标系。
3. BD09坐标系：百度坐标系，GCJ02坐标系经加密后的坐标系。
   
   图1 GPS组网，来源北斗导航系统官网

一般而言，GPS中的坐标为WGS84坐标系（《大地测量学基础》350页）。

GPS接收的坐标，一般通过对GPGGA 或者 GNGGA的信号解析得到经纬度和高程信息，两者遵循统一的标准，解析格式详见GPGGA格式详解。标准来源于NMEA 1803。

NMEA 0183是用于海洋电子设备之间通信的电气和数据规范，如回声探测仪、声纳、风速计、陀螺罗盘、自动驾驶仪、GPS接收器和许多其他类型的仪器。它由国家海洋电子协会(NMEA)定义和控制。

1.2 工程坐标系

施工一般是局部 施工，采用平面直角坐标来进行表达，因此，出现了工程坐标系。它实际是设计、施工 时采用的一种平面投影坐标系。我们工程中产生了一些和上述地心坐标系相同的叫法，本质上是由椭球+投影构成，通常而言：。

• 北京 54，多数是指：北京 54 椭球+高斯投影
• 西安 80，多数是指：西安 80 椭球+高斯投影
• 国家 2000，多数是指：国家 2000 椭球+高斯投影

坐标系之间转换方式，也会有：

• 三参数
• 四参数+高程拟合
• 七参数
• 一步法

那么，这些坐标系、投影方式、转换方式在经纬度坐标转换为工程坐标有什么作用？

2. 坐标系统

2.1 椭球

上述的各种坐标系他们都属于坐标系统，是描述地球上一点位置的不同表达。我们在描述地球时，把地球简化为一个椭球。在数学上，这个椭球通过一些几何参数确定，例如，长半轴、短半轴、扁率、偏心率等。现在坐标系中常用的椭球有：

表1 常见椭球参数

参数	克拉索夫斯基椭球体	1975年国际椭球体	WGS-84 椭球体	2000中国大地坐标系(CGCS2000)
a	6 378 245(m)	6 378 140(m)	6 378 137(m)	6 378 137(m)
b	6 356 863.018 773 047 3(m)	6 356 755.288 157 528 7(m)	6 356 752. 314 2(m)	6 356 752. 314 1(m)
c	6 399 698.901 782 711 0(m)	6 399 596.651 988 010 5(m)	6 399 593.625 8(m)	6 399 593.625 9(m)
$\alpha$	1/298.3	1/298.257	1/298.257 223 563	1/298.257 222 101
$e^2$	0.006 693 421 622 966	0. 006 694 384 999 588	0. 006 694 379 990 13	0. 006 694 380 022 90
$e^{\prime 2}$	0.006 738 525 414 683	0. 006 739 501 819 473	0.006 739 496 742 27	0. 006 739 496 775 48

图2 不规则地球的椭圆描述

2.2 椭球面上的坐标系

想要描述椭球上点的位置，就需要建立坐标系。坐标系统分为：天球坐标系和地球坐标系。地球坐标系又叫做地固坐标系。

• 天球坐标系，研究天体和人造卫星的定位和运动。 本文不予讨论。
• 地球坐标系，研究地球大气内物体的定位和运动。分为大地坐标系 和 空间直角坐标系。同时，也可以分为地心坐标系 和 参心坐标系。

所谓地心坐标系，原点与地球质心重合，以地球椭球为基准
所谓参心坐标系，原点与参考椭球中心重合，以参考椭球为基准

因此，无论是地心坐标系 还是 参心坐标系，均可分为大地坐标系 和 空间直角坐标系两种。这两种坐标之间的相互关系和推导过程，参见charlee44的博客2.1节。可见，他们之间可以相互转换。

常见的参心坐标系：

• 1954年北京坐标系（北京54坐标系）
• 1980年国家大地坐标系（西安80坐标系）
• 新1954年北京坐标系（BJ54_新）

常见的地心坐标系：

• WGS-84世界大地坐标系（WGS84）
• CGCS2000中国大地坐标系

但是，这里所说的空间直角坐标系，并不是我们工程中经常见到的直角坐标系。它的坐标原点在图3所示的球心。此球心可以是地球质心（地心坐标系）也可以是椭球中心（参心坐标系）。

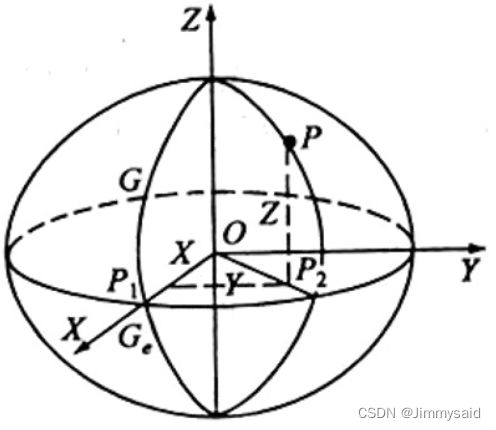
图3 空间直角坐标系

2.3 投影

说起投影，就涉及到地图数学投影，简单的说就是将表1所列举的某个椭球面上的坐标、方位、距离按照一定的数学法则投影到平面：
$$\{\begin{array}{rl}x& =F_1(L,B)\\ y& =F_2(L,B)\end{array}$$
式中，$F_1$、$F_2$是投影函数；$L$，$B$是椭球面上某点的大地坐标；$x$，$y$是该点投影后的平面直角坐标，这里的平面也叫投影面。
其实这样的坐标系我们生活中就可以见到，例如，办公室内挂着的全国地图。

投影按照不同的方式 有很多种的分类，具体可以参见《大地测量学基础》157页。现在很多国家使用高斯-克里格投影。

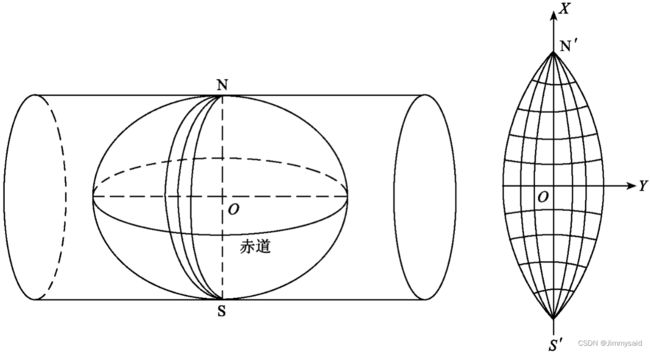
高斯平面直角坐标系

高斯平面直接坐标系，以中央子午线的投影为纵轴，以赤道的投影为横轴，两交点为原点。
有时候，会说投影按照某一带去投影。这里的“带”是指

测量上将很大的区域按照一定的规律分成若干小区域，又叫带。

它的出现，是因为毕竟是曲面到平面的投影，必然会产生变形。在某些区域，这样的变形很大。为了避免大变形带来的扭曲，我们把区域按照一定的规律分成若干小区域，在小区域中去投影。

我国按照经差6°和3°进行投影分带。

图4 高斯克里格投影

在我国x坐标都是正数，y最大值约为330km。为避免出现负的横坐标，一般加了500km。例如$Y=19123456.789m$，代表在19带内，其相对中央子午线的横坐标是：去掉带号19，再减去500km，得到$Y=-376543.211m$。

因此，利用高斯投影函数，可将上述大地坐标系的坐标转换为在高斯投影下的平面坐标。

3. 坐标系与投影方式的关系

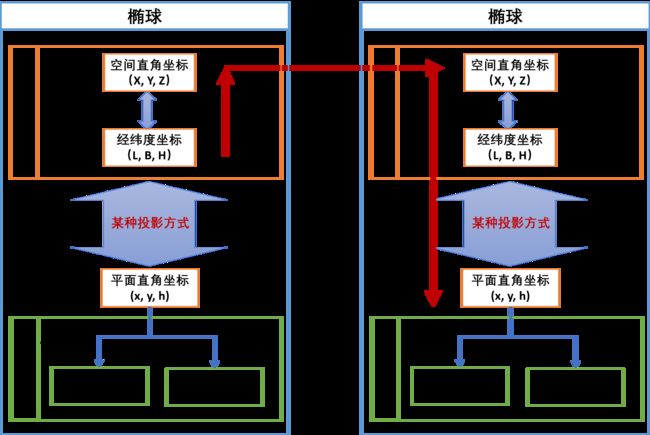
据此，可以将上述 大地坐标系、投影方式之间的关系用如下表示：

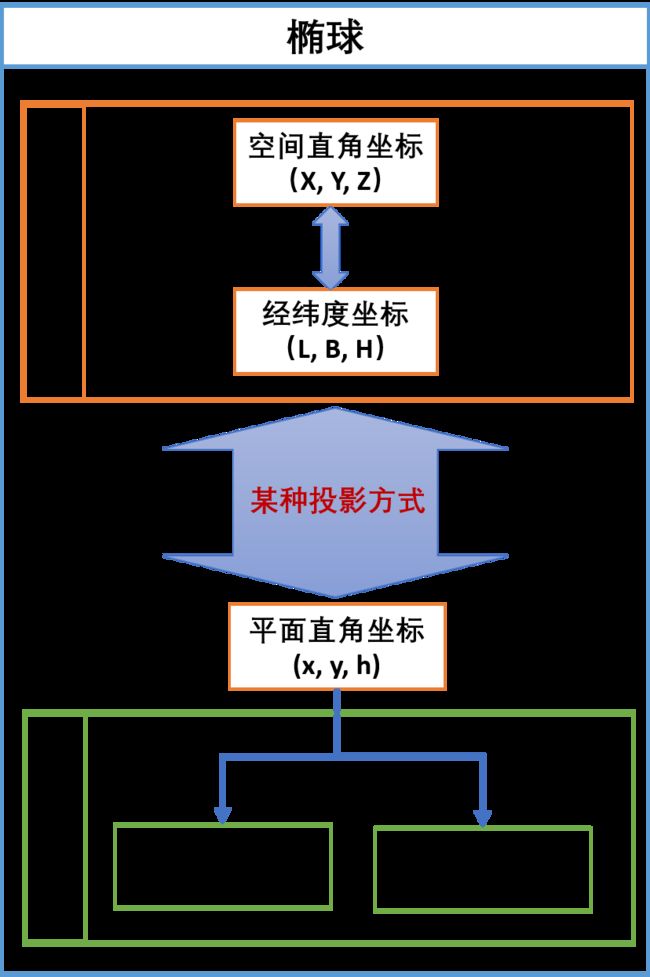
图5 大地坐标系与投影关系

上图中，空间直角坐标 与 经纬度坐标 可以按照charlee44的博客2.1节方式转换。
某种投影方式，一般为高斯-克里格投影。
当地坐标系中，按照工程需求，如果高程可以忽略，则可以经过平面转换，使用当地平面坐标。

4. 经纬度坐标转换为工程坐标

至此，经纬度坐标转换为工程坐标这一过程可以按照如下步骤：

1. GPS接收信号坐标为WGS-84大地坐标系的经纬度坐标$(L_{source},B_{source},H_{source})$
2. 利用charlee44的博客2.1节，将经纬度坐标$(L_{source},B_{source},H_{source})$转换为空间直角坐标系$(X_{source},Y_{source},Z_{source})$
3. 确定工程坐标所使用的大地坐标系所属目标椭球和投影方式
4. 利用7参数，将$(X_{source},Y_{source},Z_{source})$转换为目标椭球下的$(X_{target},Y_{target},Z_{target})$
5. 利用charlee44的博客2.2节，将空间直角坐标系$(X_{target},Y_{target},Z_{target})$转换为经纬度坐标$(L_{target},B_{target},H_{target})$
6. 利用投影方式，将经纬度转换为当地坐标系下的坐标