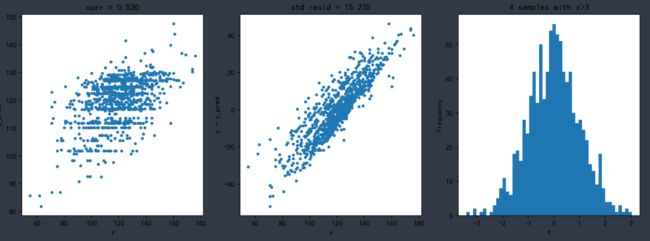
机器学习案例：孕妇吸烟与胎儿健康

导言

• 最近在入门机器学习，学了一段时间觉得需要尝试做一个案例，巩固学过的知识，查漏补缺。
• 想到刚刚入门数学建模时《数学模型》中统计学习的第一章，孕妇吸烟与胎儿健康问题。数据集在这
• 这里以孕妇吸烟与胎儿健康为例，建立模型，希望通过各类特征预测新生儿体重。（注：因为此问题中各特征与新生儿体重间并无强烈相关性，导致各类模型效果可能都不会特别理想，这里只讨论方法）
• 代码我基本一行一行注释，应该不会出现看不明白的情况。

数据处理

导入包

#加载包
import numpy as np
import pandas as pd
from plotnine import*
from scipy import stats
import seaborn as sns
import statsmodels.api as sm
import matplotlib as mpl
import matplotlib.pyplot as plt
#中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# notebook嵌入图片
%matplotlib inline
# 提高分辨率
%config InlineBackend.figure_format='retina'

from sklearn.model_selection import learning_curve
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV, RepeatedKFold, cross_val_score,cross_val_predict,KFold
from sklearn.metrics import make_scorer,mean_squared_error
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.svm import LinearSVR, SVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor,AdaBoostRegressor
from xgboost import XGBRegressor
from sklearn.preprocessing import PolynomialFeatures,MinMaxScaler,StandardScaler

# 忽略警告
import warnings
warnings.filterwarnings('ignore')

导入数据

name = ['序号','新生儿体重','孕妇怀孕期','新生儿胎次状况','孕妇怀孕时年龄','孕妇怀孕前身高','孕妇怀孕前体重','孕妇吸烟状况']
data = pd.read_csv("D:/学习资料/数学/数学建模培训与比赛/孕妇吸烟与胎儿健康/data0901.txt", sep = '\t',names = name,encoding="gbk",index_col = '序号')
data.head()

输出：

检查数据类型

data.dtypes

输出：

计算基础统计量

data.describe()

输出：

剔除缺失值

• 文中提到，使用9、99、999标记缺失值，我们直接剔除缺失样本。

# 剔除缺失值
data = data[(data['孕妇吸烟状况'] < 9) &
            (data['孕妇怀孕前体重'] < 999) & 
            (data['孕妇怀孕前身高'] < 99) & 
            (data['孕妇怀孕时年龄'] < 99) & 
            (data['孕妇怀孕期'] < 999)]

异常值检查

• 使用箱型图进行异常值检查

# 绘制箱型图进行异常值检查
i = 0
frows = 2
fcols = 2
plt.figure(figsize=(12, 8))
for lab in data.columns[[1,3,4,5]]:
    i += 1
    plt.subplot(frows,fcols,i)
    plt.boxplot(x=data[lab].values,labels=[lab])

输出：

检查线性相关性

# 获取列标签
column = data.columns.tolist()  
mcorr = data[column].corr(method="spearman")  
mcorr=mcorr.abs()
numerical_corr=mcorr['新生儿体重']
index0 = numerical_corr.sort_values(ascending=False).index

# 将各变量与结果相关性的降序排列赋值给features_corr
features_corr = numerical_corr.sort_values(ascending=False).reset_index()
# 更改features_corr列标签
features_corr.columns = ['features_and_wight', 'corr']
features_corr

输出：

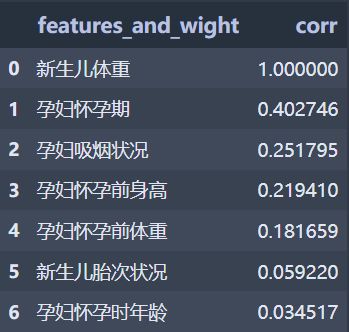
特征优化

确定组合形式

epsilon=1e-5

#组交叉特征，可以自行定义，如增加： x*x/y, log(x)/y 等等
func_dict = {
            'add': lambda x,y: x+y,
            'mins': lambda x,y: x-y,
            'div': lambda x,y: x/(y+epsilon),
            'multi': lambda x,y: x*y
            }

定义组合函数

def auto_features_make(train_data,func_dict,col_list):
    # 将训练样本复制
    train_data = train_data.copy()
    # 遍历列索引
    for col_i in col_list:
        cs = col_list[col_list != col_i]
        # 遍历列索引
        for col_j in cs:
            # 遍历操作名称，匿名函数
            for func_name, func in func_dict.items():
                # 将训练样本的副本赋值给data
                data = train_data
                # 将两列标签进行特征组合
                func_features = func(data[col_i],data[col_j])
                # 命名新列
                col_func_features = '-'.join([col_i,func_name,col_j])
                data[col_func_features] = func_features
    return train_data

基于原始数据进行组合

# 将除'新生儿体重'以外的非0,1变量列进行特征组合
data_temp = auto_features_make(data,func_dict,col_list=data.columns[[1,3,4,5]])
data = data_temp
data.shape

输出：

(1174, 55)

• 这里可以看到组合后的变量达到了55个

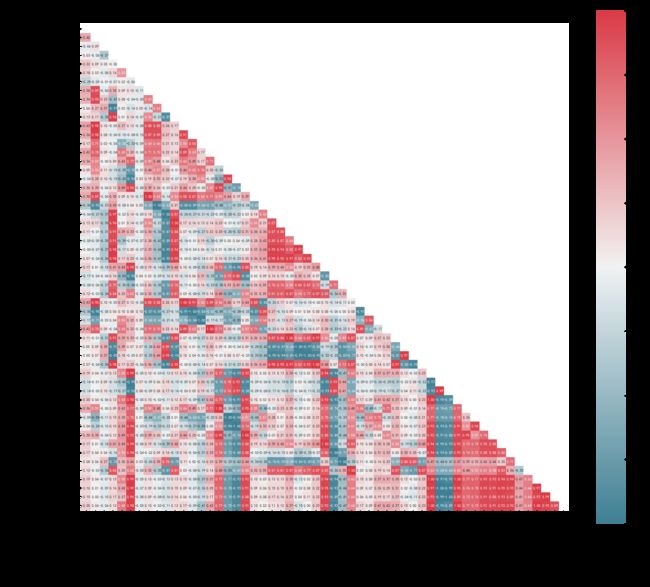
绘制相关性热力图

# 绘制相关性热力图
plt.figure(figsize=(30, 26))
# 获取列标签
column = data.columns.tolist()  
mcorr = data[column].corr(method="spearman")  
# 创建一个和相关性矩阵相同维度的空矩阵
mask = np.zeros_like(mcorr, dtype=np.bool)  
mask[np.triu_indices_from(mask)] = True  
cmap = sns.diverging_palette(220, 10, as_cmap=True)  
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')  
plt.savefig('2.png')
plt.show()

输出：

特征降维

# 取相关性矩阵的绝对值
mcorr=mcorr.abs()
# 筛选与新生儿体重相关性大于0.1的变量
numerical_corr=mcorr[mcorr['新生儿体重']>0.1]['新生儿体重']
index0 = numerical_corr.sort_values(ascending=False).index

# 将各变量与结果相关性的降序排列赋值给features_corr
features_corr = numerical_corr.sort_values(ascending=False).reset_index()
# 更改features_corr列标签
features_corr.columns = ['features_and_wight', 'corr']
# 筛选出大于相关性大于0.3的特征
features_corr_select = features_corr[features_corr['corr']>0.3] 
features_corr_select

输出：

特征提取

# 将除结果列的其他相关性大于0.3的列提取出来
select_features = [col for col in features_corr_select['features_and_wight'] if col not in ['新生儿体重']]
# 提取
data = data[['新生儿体重']+select_features]
data

数据归一化

from sklearn import preprocessing 

features_columns = [col for col in data.columns if col not in ["新生儿体重"]]

min_max_scaler = preprocessing.MinMaxScaler()

min_max_scaler = min_max_scaler.fit(data[features_columns])

data_scaler = min_max_scaler.transform(data[features_columns])

data_scaler = pd.DataFrame(data_scaler)
data_scaler.columns = features_columns
temp = pd.DataFrame(np.array(data["新生儿体重"]))

data_scaler['新生儿体重'] = temp[0]
data = data_scaler[['新生儿体重']+features_columns]

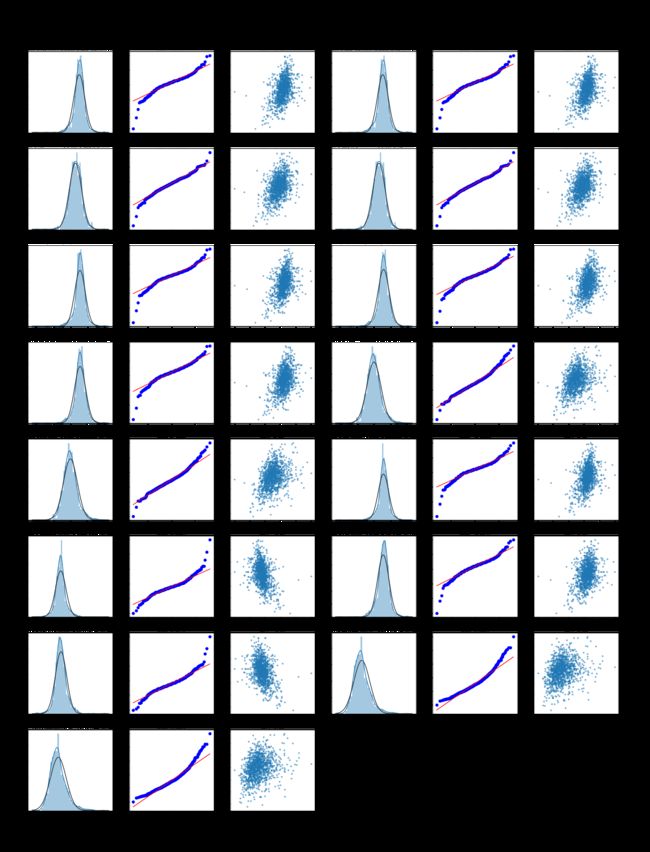
绘制数据分布图与QQ图

# 一行6个子图
cols_numeric=list(data.iloc[:,1:].columns)
fcols = 6
# 一列len(cols_numeric)-1个子图，剔除结果target列
frows = len(cols_numeric)
plt.figure(figsize=(4*fcols,4*frows))
i=0

for var in cols_numeric:
    # dropna()删除所有包含NaN的行
    # 按顺序取列标签和结果列，组成表
    dat = data[[var, '新生儿体重']].dropna()
        
    i+=1
    # 子图顺序
    plt.subplot(frows,fcols,i)
    # 绘制特征列核密度估计图
    sns.distplot(dat[var] , fit=stats.norm);
    plt.title(var+' Original')
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    # 绘制特征列QQ图
    _=stats.probplot(dat[var], plot=plt)
    # stats.skew计算数据集的偏度
    plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    # 绘制散点图
    plt.plot(dat[var], dat['新生儿体重'],'.',alpha=0.5)
    # 计算与结果列的相关性
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var], dat['新生儿体重'])[0][1]))
plt.savefig('3.png')

输出：

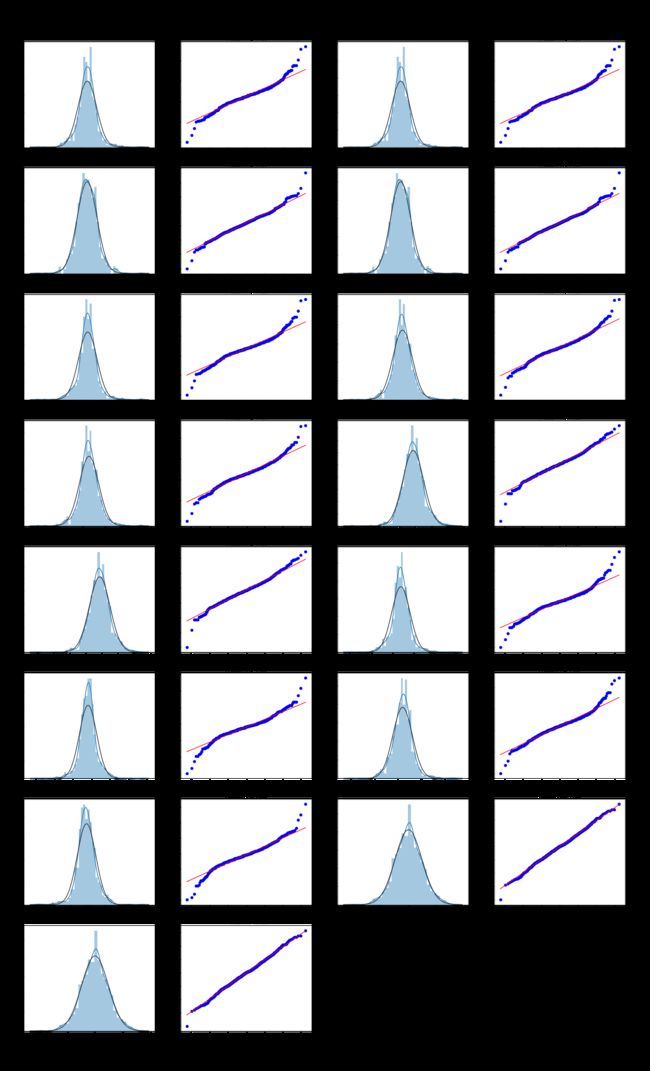
Box-Cox变换

• Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法，是统计建模中常用的一种数据变换，用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的（引自百度百科）

数据变换

# box变换使数据更具有正态性
# 去除'新生儿体重列'
cols_transform=data.columns[1:]
for col in cols_transform:   
    # transform column
    data.loc[:,col], _ = stats.boxcox(data.loc[:,col]+1)

可视化展示

# 一行4个子图
fcols = 4
# 一列len(cols_numeric)-1个子图，剔除结果target列
frows = len(cols_transform)
plt.figure(figsize=(25,80))
i=0
for temp in cols_transform:
    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(data[temp], fit=stats.norm)
    
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(data[temp], plot=plt)
plt.savefig('4.png')

输出：

划分数据集

• 将数据集划分为测试集与训练集，其中训练集占数据集的80%，测试集占数据集的20%。

# 划分训练集与测试集
X_train,X_valid,y_train,y_valid=train_test_split(data.iloc[:,1:],data.iloc[:,0],test_size=0.2,random_state=42)

模型建立

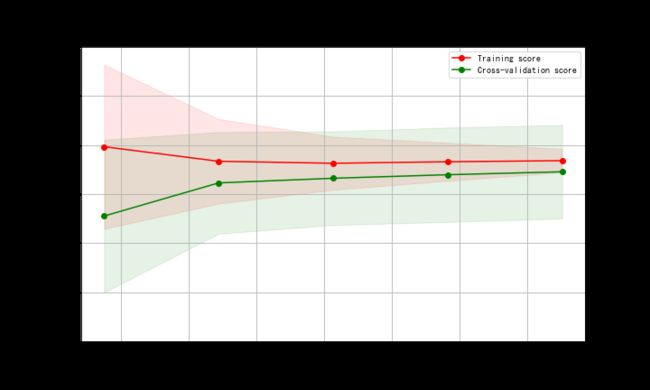
绘制学习曲线函数

• 其中有两个函数需要注意：learning_curve()函数、fill_between()函数
• learning_curve()函数参数及含义解释，参照
• fill_between()函数参数及含义解释，参照

# 绘制学习曲线
# 输入参数：模型，名称，自变量，因变量，绘图时y轴的上下限，交叉验证折数，要并行运行的作业数，训练示例的相对或绝对数量
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
                        n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
    # 画布大小
    plt.figure(figsize=(10,6))
    # 图标题
    plt.title(title)
    if ylim is not None:
        plt.ylim(*ylim)
    # x轴标题
    plt.xlabel("Training examples")
    # y轴标题
    plt.ylabel("Score")
    # learning_curve学习曲线函数
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    # 输出训练集的平均分
    print(train_scores_mean)
    # 输出测试集的平均分
    print(test_scores_mean)
    # 为图形添加网格
    plt.grid()
    # fill_between()函数用于阴影形成
    # 训练集曲线
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,
                     color="r")
    # 测试集学习曲线
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1, color="g")
    # 测试集平均得分
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
             label="Training score")
    # 训练集平均得分
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")
 
    plt.legend(loc="best")
    return plt

建立岭回归模型

• 评估模型分数的指标为：mse

# 构建岭回归模型
from sklearn.linear_model import RidgeCV
# 建立模型
ridge = RidgeCV(alphas=np.arange(0.5,3.1,0.5))
ridge.fit(X_train, y_train)
# 计算模型在测试集上分数
score_mse = mean_squared_error(y_valid, ridge.predict(X_valid))
print("alpha:   ",ridge.alpha_)
print("Ridge_mse:   ", score_mse)

输出：

alpha:    2.0
Ridge_mse:    293.99217110325054

学习曲线

X = X_train
y = y_train

title = r"Ridge"
from sklearn.model_selection import ShuffleSplit
# ShuffleSplit随机排列交叉验证
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = RidgeCV(alphas=np.arange(0.5,3.1,0.5))    #建模
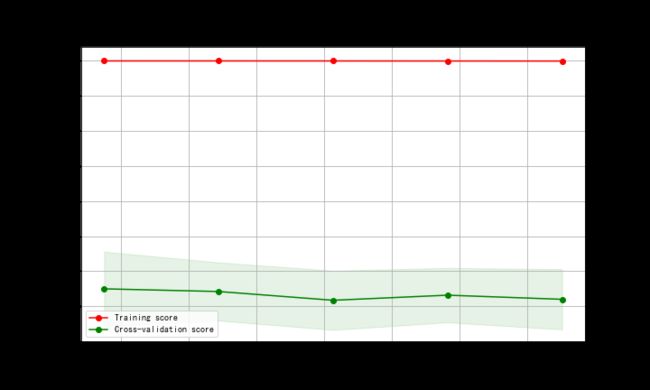
plot_learning_curve(estimator, title, X, y, ylim=(0, 0.3), cv=cv, n_jobs=1)

输入：

建立K邻近回归模型

knn = KNeighborsRegressor(n_neighbors=11)
knn.fit(X_train, y_train)
score_mse = mean_squared_error(y_valid, knn.predict(X_valid))
print("KNN_mse:   ", score_mse)

输出：

KNN_mse:    273.5592052048532

学习曲线

X = X_train
y = y_train
 
title = r"KNeighborsRegressor"
from sklearn.model_selection import ShuffleSplit
# ShuffleSplit随机排列交叉验证
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = KNeighborsRegressor(n_neighbors=11)    #建模
plot_learning_curve(estimator, title, X, y, ylim=(0, 0.4), cv=cv, n_jobs=1)

输出：

决策树回归模型

from sklearn.tree import DecisionTreeRegressor     #决策树回归
decis = DecisionTreeRegressor()
decis.fit(X_train, y_train)
score_mse = mean_squared_error(y_valid, decis.predict(X_valid))
print("Decis_mse:   ", score_mse)

输出：

Decis_mse:    574.3234042553191

学习曲线

X = X_train
y = y_train
 
title = r"DecisionTreeRegressor"
from sklearn.model_selection import ShuffleSplit
# ShuffleSplit随机排列交叉验证
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = DecisionTreeRegressor()    #建模
plot_learning_curve(estimator, title, X, y, ylim=(-1, 1.1), cv=cv, n_jobs=1)

输出：

总结

• 以上构建的为简单模型，并且未进行任何调参处理。

模型	在测试集上MSE
岭回归	293.99
K邻近回归	273.55
决策树回归	574.32

• 可以看到三种简单模型中岭回归模型在测试集上表现最好，而决策树表现最差。
• 下面对其他模型进行调参与优化。

定义模型评分函数

# 定义模型评估分数
from sklearn.metrics import make_scorer

def rmse(y_true, y_pred):
    diff = y_pred - y_true
    sum_sq = sum(diff**2)    
    n = len(y_pred)   
    
    return np.sqrt(sum_sq/n)
def mse(y_ture,y_pred):
    return mean_squared_error(y_ture,y_pred)

# 拟合过程中使用的评估器
rmse_scorer = make_scorer(rmse, greater_is_better=False)
mse_scorer = make_scorer(mse, greater_is_better=False)

定义模型训练与评估函数

from sklearn.preprocessing import StandardScaler
# 输入参数为：模型，网格搜索集合，自变量，因变量，交叉检验折数，交叉检验重复次数
def train_model(model, param_grid=[], X=[], y=[], 
                splits=5, repeats=5):
    # RepeatedKFold函数：K折交叉检验
    rkfold = RepeatedKFold(n_splits=splits, n_repeats=repeats)
    # 如果网格搜索集合不为空
    if len(param_grid)>0:
        # 准备网格搜索
        gsearch = GridSearchCV(model, param_grid, cv=rkfold,
                               scoring="neg_mean_squared_error",
                               verbose=1, return_train_score=True)

        # 网格搜索
        gsearch.fit(X,y)

        # 固定最优网络(输出值)
        model = gsearch.best_estimator_        
        best_idx = gsearch.best_index_

        # 获得最佳模型的分数(输出值)
        grid_results = pd.DataFrame(gsearch.cv_results_)     
        # 模型平均得分(越高越好)
        cv_mean = abs(grid_results.loc[best_idx,'mean_test_score'])
        # 模型得分标准差(越低越好)
        cv_std = grid_results.loc[best_idx,'std_test_score']

    # 没有网格搜索，只需对给定模型进行评分 
    else:
        grid_results = []
        cv_results = cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=rkfold)
        cv_mean = abs(np.mean(cv_results))
        cv_std = np.std(cv_results)
    
    # 将平均值和分数组合成一个表(输出值)
    cv_score = pd.Series({'mean':cv_mean,'std':cv_std})

    # 利用最优模型得到测试集的预测值
    y_pred = model.predict(X)
    
    # 打印输出
    print('----------------------')
    # 输出网格搜索中的最优参
    print(gsearch.best_params_)
    print('----------------------')
    print('score=',model.score(X,y))
    print('rmse=',rmse(y, y_pred))
    print('mse=',mse(y, y_pred))
    print('cross_val: mean=',cv_mean,', std=',cv_std)
    
    # 将测试集预测值转换为一维数组(基于Numpy的ndarray),行标签不变
    y_pred = pd.Series(y_pred,index=y.index)
    # 计算残差
    resid = y - y_pred
    # 计算残差绝对值
    mean_resid = resid.mean()
    # 计算残差标准差
    std_resid = resid.std()
    # 标准化残差
    z = (resid - mean_resid)/std_resid    
    # 大于3sigma的为粗大误差
    n_outliers = sum(abs(z)>3)
    
    # 设置画布大小
    plt.figure(figsize=(15,5))
    
    # 相关系数散点图
    ax_131 = plt.subplot(1,3,1)
    # x轴为测试集真实结果，y轴为预测结果
    plt.plot(y,y_pred,'.')
    plt.xlabel('y')
    plt.ylabel('y_pred');
    # 计算相关系数
    plt.title('corr = {:.3f}'.format(np.corrcoef(y,y_pred)[0][1]))
    
    # 残差图
    ax_132=plt.subplot(1,3,2)
    plt.plot(y,y-y_pred,'.')
    plt.xlabel('y')
    plt.ylabel('y - y_pred');
    plt.title('std resid = {:.3f}'.format(std_resid))
    
    # 标准化残差的直方图
    ax_133=plt.subplot(1,3,3)
    z.plot.hist(bins=50,ax=ax_133)
    plt.xlabel('z')
    plt.title('{:.0f} samples with z>3'.format(n_outliers))
    # 返回模型，交叉检验分数，最优网络返回值
    return model, cv_score, grid_results

定义默认参数

# 存储最佳模型及分数
# dict()函数，生成字典
opt_models = dict()
score_models = pd.DataFrame(columns=['mean','std'])

# 要划分的折数(默认值)
splits=10
# 迭代次数(默认值)
repeats=5

Lasso回归模型

model = 'Lasso'

opt_models[model] = Lasso()
alph_range = np.arange(1e-4,1e-3,4e-5)
param_grid = {'alpha': alph_range}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid,
                                                        X = X_train, y = y_train,
                                              splits=splits, repeats=repeats)

cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(alph_range, abs(grid_results['mean_test_score']),abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('alpha')
plt.ylabel('score')

输出：

Fitting 50 folds for each of 23 candidates, totalling 1150 fits
----------------------
{'alpha': 0.0009800000000000002}
----------------------
score= 0.18601358023857617
rmse= 16.17030489660215
mse= 261.4787604490757
cross_val: mean= 265.6104966889251 , std= 40.643975957336544

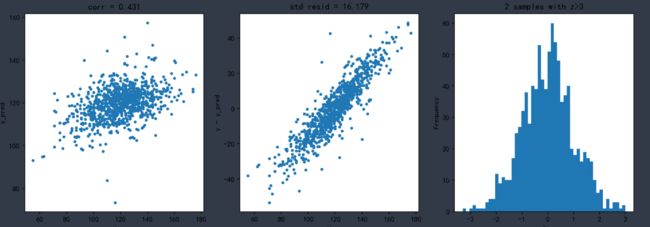
结果可视化

ElasticNet回归模型

model ='ElasticNet'
opt_models[model] = ElasticNet()

param_grid = {'alpha': np.arange(1e-4,1e-3,1e-4),
              'l1_ratio': np.arange(0.1,1.0,0.1),
              'max_iter':[100000]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                                        X = X_train, y = y_train,
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

输出：

----------------------
{'alpha': 0.0009000000000000001, 'l1_ratio': 0.1, 'max_iter': 100000}
----------------------
score= 0.18478760823526608
rmse= 16.182477631735292
mse= 261.8725823016132
cross_val: mean= 265.4672534048344 , std= 30.190083240495404

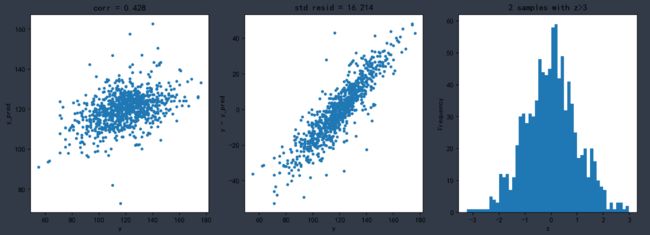
结果可视化

SVR回归模型

model='LinearSVR'
opt_models[model] = LinearSVR()

crange = np.arange(16,21,1)
param_grid = {'C':crange,
             'max_iter':[1000]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                                         X = X_train, y = y_train,
                                              splits=splits, repeats=repeats)


cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(crange, abs(grid_results['mean_test_score']),abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('C')
plt.ylabel('score')

输出：

Fitting 50 folds for each of 5 candidates, totalling 250 fits
----------------------
{'C': 19, 'max_iter': 1000}
----------------------
score= 0.18226265038475586
rmse= 16.20751925540868
mse= 262.68368041444296
cross_val: mean= 265.14517245054805 , std= 32.50920665687631

结果可视化

集成学习Boosting模型

model = 'GradientBoosting'
opt_models[model] = GradientBoostingRegressor()

param_grid = {'n_estimators':np.arange(200,301,10),
              'max_depth':[1,2,3],
              'min_samples_split':[2,3,4]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                                        X = X_train, y = y_train,
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

输出：

Fitting 10 folds for each of 99 candidates, totalling 990 fits
----------------------
{'max_depth': 1, 'min_samples_split': 2, 'n_estimators': 220}
----------------------
score= 0.29654627870797934
rmse= 15.032367855102477
mse= 225.97208333111834
cross_val: mean= 260.88322945349813 , std= 41.78155070729958

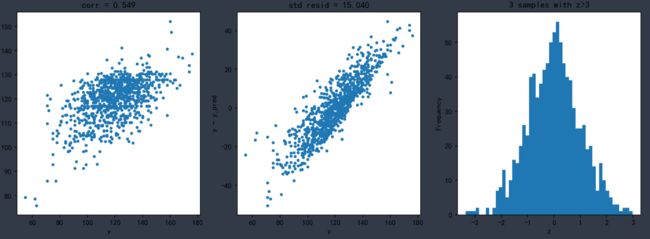
结果可视化

集成学习xgboost模型

model = 'XGB'
opt_models[model] = XGBRegressor()

param_grid = {'n_estimators':np.arange(40,61,5),
              'max_depth':[1,2,3],
             }

opt_models[model], cv_score,grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                                       X = X_train, y = y_train,
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

输出：

Fitting 10 folds for each of 15 candidates, totalling 150 fits
----------------------
{'max_depth': 1, 'n_estimators': 50}
----------------------
score= 0.27819320903214373
rmse= 15.227202067564829
mse= 231.86768280645057
cross_val: mean= 259.6649297403458 , std= 46.54327232363794

结果可视化

随机森林回归模型

model = 'RandomForest'
opt_models[model] = RandomForestRegressor()

param_grid = {'n_estimators':np.arange(190,195,1),
              'max_features':np.arange(1,3,1),
              'min_samples_split':[5,7,9]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                                        X = X_train, y = y_train,
                                              splits=5, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

输出：

Fitting 5 folds for each of 30 candidates, totalling 150 fits
----------------------
{'max_features': 1, 'min_samples_split': 7, 'n_estimators': 191}
----------------------
score= 0.6761201603637153
rmse= 10.200033235707894
mse= 104.04067800954564
cross_val: mean= 267.41833075031957 , std= 21.408381740568544

结果可视化

定义各模型预测函数

# 输入参数为：测试集自变量，测试集因变量
def model_predict(test_data,test_y=[],stack=False):
    i=0
    # 创建与测试集行数相等的1列空向量
    y_predict_total=np.zeros((test_data.shape[0],))
    # 字典中的k表示键，即各类模型的名字
    for model in opt_models.keys():
        # 如果模型不为K邻近和SVR回归模型
        if model!="LinearSVR" and model!="KNeighbors":
            y_predict=opt_models[model].predict(test_data)
            y_predict_total+=y_predict
            i+=1
        # 如果测试集有真实值输入
        if len(test_y)>0:
            # 计算与真实值的mse
            print("{}_mse:".format(model),mean_squared_error(y_predict,test_y))
    # 对平均值小数点3位进行四舍五入操作
    y_predict_mean=np.round(y_predict_total/i,3)
    if len(test_y)>0:
        # 输出模型平均mse
        print("mean_mse:",mean_squared_error(y_predict_mean,test_y))
    else:
        y_predict_mean=pd.Series(y_predict_mean)
        return y_predict_mean

各模型在测试集上表现

model_predict(X_valid,y_valid)

输出：

Lasso_mse: 293.54406861378794
ElasticNet_mse: 294.06036201775856
LinearSVR_mse: 294.06036201775856
GradientBoosting_mse: 265.33372076064626
XGB_mse: 268.5055199887331
RandomForest_mse: 287.10684591621344
mean_mse: 275.1018021319149

• 可以看到，集成学习方法中xgboost模型、Boosting模型在测试集上的表现明显优于其他模型，其次是随机深林模型。这里倒是充分证明了“三个臭皮匠顶个诸葛亮”