神经网络与深度学习作业8：RNN - 简单循环网络

---

  简单循环网络 （ Simple Recurrent Network ， SRN） 只有一个隐藏层的神经网络 。

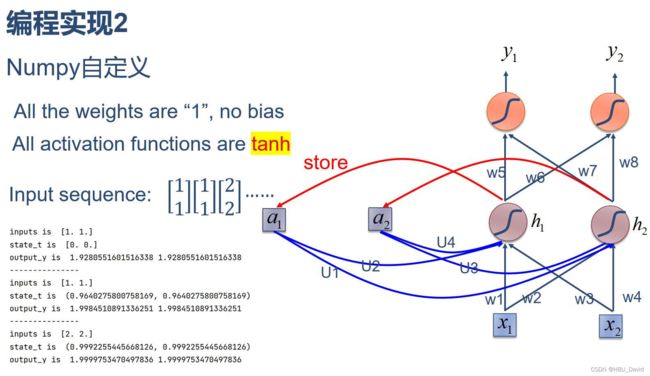
1. 使用Numpy实现SRN

import numpy as np

inputs = np.array([[1., 1.],
                   [1., 1.],
                   [2., 2.]])  # 初始化输入序列
print('inputs is ', inputs)

state_t = np.zeros(2, )  # 初始化存储器
print('state_t is ', state_t)

w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
    print('inputs is ', input_t)
    print('state_t is ', state_t)
    in_h1 = np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t)
    in_h2 = np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t)
    state_t = in_h1, in_h2
    output_y1 = np.dot([w5, w7], [in_h1, in_h2])
    output_y2 = np.dot([w6, w8], [in_h1, in_h2])
    print('output_y is ', output_y1, output_y2)
    print('---------------')

 运行结果如图：

2. 在1的基础上，增加激活函数tanh

import numpy as np
 
inputs = np.array([[1., 1.],
                   [1., 1.],
                   [2., 2.]])  # 初始化输入序列
print('inputs is ', inputs)
 
state_t = np.zeros(2, )  # 初始化存储器
print('state_t is ', state_t)
 
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
    print('inputs is ', input_t)
    print('state_t is ', state_t)
    in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
    in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
    state_t = in_h1, in_h2
    output_y1 = np.dot([w5, w7], [in_h1, in_h2])
    output_y2 = np.dot([w6, w8], [in_h1, in_h2])
    print('output_y is ', output_y1, output_y2)
    print('---------------')

 运行结果如图

3. 分别使用nn.RNNCell、nn.RNN实现SRN

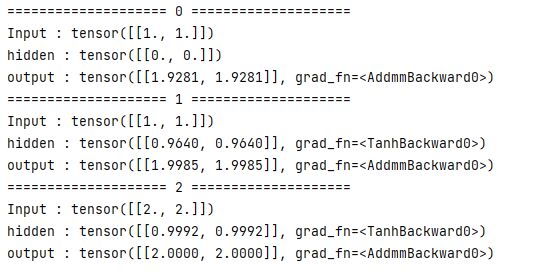
 使用nn.RNNCell实现SRN：

import torch
 
batch_size = 1
seq_len = 3  # 序列长度
input_size = 2  # 输入序列维度
hidden_size = 2  # 隐藏层维度
output_size = 2  # 输出层维度
 
# RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# 初始化参数 https://zhuanlan.zhihu.com/p/342012463
for name, param in cell.named_parameters():
    if name.startswith("weight"):
        torch.nn.init.ones_(param)
    else:
        torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
 
seq = torch.Tensor([[[1, 1]],
                    [[1, 1]],
                    [[2, 2]]])
hidden = torch.zeros(batch_size, hidden_size)
output = torch.zeros(batch_size, output_size)
 
for idx, input in enumerate(seq):
    print('=' * 20, idx, '=' * 20)
 
    print('Input :', input)
    print('hidden :', hidden)
 
    hidden = cell(input, hidden)
    output = liner(hidden)
    print('output :', output)

 运行结果如图：

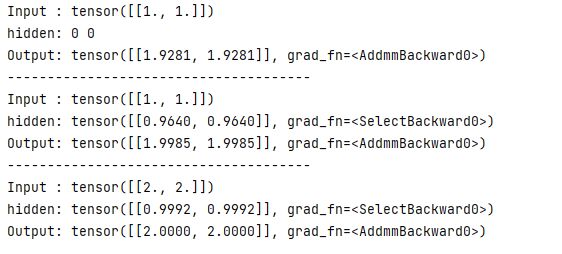
 使用torch.nn.RNN：

import torch
 
batch_size = 1
seq_len = 3
input_size = 2
hidden_size = 2
num_layers = 1
output_size = 2
 
cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)
for name, param in cell.named_parameters():  # 初始化参数
    if name.startswith("weight"):
        torch.nn.init.ones_(param)
    else:
        torch.nn.init.zeros_(param)
 
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
 
inputs = torch.Tensor([[[1, 1]],
                       [[1, 1]],
                       [[2, 2]]])
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
 
print('Input :', inputs[0])
print('hidden:', 0, 0)
print('Output:', liner(out[0]))
print('--------------------------------------')
print('Input :', inputs[1])
print('hidden:', out[0])
print('Output:', liner(out[1]))
print('--------------------------------------')
print('Input :', inputs[2])
print('hidden:', out[1])
print('Output:', liner(out[2]))

 运行结果如图：

4. 分析“二进制加法” 源代码

 源代码：

import copy, numpy as np

np.random.seed(0)


#定义sigmoid函数
def sigmoid(x):
    output = 1 / (1 + np.exp(-x))
    return output


#定义sigmoid导数
def sigmoid_output_to_derivative(output):
    return output * (1 - output)


#训练数据的产生
int2binary = {}
binary_dim = 8 #定义二进制位的长度

largest_number = pow(2, binary_dim)#定义数据的最大值
binary = np.unpackbits(
    np.array([range(largest_number)], dtype=np.uint8).T, axis=1)#函数产生包装所有符合的二进制序列
for i in range(largest_number):#遍历从0-256的值
    int2binary[i] = binary[i]#对于每个整型值赋值二进制序列
print(int2binary)
# 产生输入变量
alpha = 0.1         #设置更新速度（学习率）
input_dim = 2       #输入维度大小
hidden_dim = 16     #隐藏层维度大小
output_dim = 1      #输出维度大小

# 随机产生网络权重
synapse_0 = 2 * np.random.random((input_dim, hidden_dim)) - 1
synapse_1 = 2 * np.random.random((hidden_dim, output_dim)) - 1
synapse_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1

#梯度初始值设置为0
synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)

#训练逻辑
for j in range(10000):

    # 产生一个简单的加法问题
    a_int = np.random.randint(largest_number / 2)  # 产生一个加法操作数
    a = int2binary[a_int]   # 找到二进制序列编码

    b_int = np.random.randint(largest_number / 2)  # 产生另一个加法操作数
    b = int2binary[b_int]   # 找到二进制序列编码

    # 计算正确值（标签值）
    c_int = a_int + b_int
    c = int2binary[c_int]   # 得到正确的结果序列

    # 设置存储器，存储中间值（记忆功能）
    d = np.zeros_like(c)

    overallError = 0        #设置误差

    layer_2_deltas = list()
    layer_1_values = list()
    layer_1_values.append(np.zeros(hidden_dim))

    # moving along the positions in the binary encoding
    for position in range(binary_dim):
        # 产生输入和输出
        X = np.array([[a[binary_dim - position - 1], b[binary_dim - position - 1]]])
        y = np.array([[c[binary_dim - position - 1]]]).T

        # 隐藏层计算
        layer_1 = sigmoid(np.dot(X, synapse_0) + np.dot(layer_1_values[-1], synapse_h))

        # 输出层
        layer_2 = sigmoid(np.dot(layer_1, synapse_1))
        # 计算差别
        layer_2_error = y - layer_2
        #计算每个梯度
        layer_2_deltas.append((layer_2_error) * sigmoid_output_to_derivative(layer_2))
        #计算所有损失
        overallError += np.abs(layer_2_error[0])

        # 编码记忆的中间值
        d[binary_dim - position - 1] = np.round(layer_2[0][0])

        # 拷贝副本
        layer_1_values.append(copy.deepcopy(layer_1))

    future_layer_1_delta = np.zeros(hidden_dim)

    for position in range(binary_dim):
        X = np.array([[a[position], b[position]]])
        layer_1 = layer_1_values[-position - 1]
        prev_layer_1 = layer_1_values[-position - 2]

        # 输出层误差
        layer_2_delta = layer_2_deltas[-position - 1]
        # 隐藏层误差
        layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(
            synapse_1.T)) * sigmoid_output_to_derivative(layer_1)

        # 计算梯度
        synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
        synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
        synapse_0_update += X.T.dot(layer_1_delta)

        future_layer_1_delta = layer_1_delta
    #梯度下降
    synapse_0 += synapse_0_update * alpha
    synapse_1 += synapse_1_update * alpha
    synapse_h += synapse_h_update * alpha
    #重新初始化
    synapse_0_update *= 0
    synapse_1_update *= 0
    synapse_h_update *= 0

    # 打印训练过程
    if (j % 1000 == 0):
        print("Error:" + str(overallError))
        print("Pred:" + str(d))
        print("True:" + str(c))
        out = 0
        for index, x in enumerate(reversed(d)):
            out += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out))
        print("------------")

 运行结果如图：

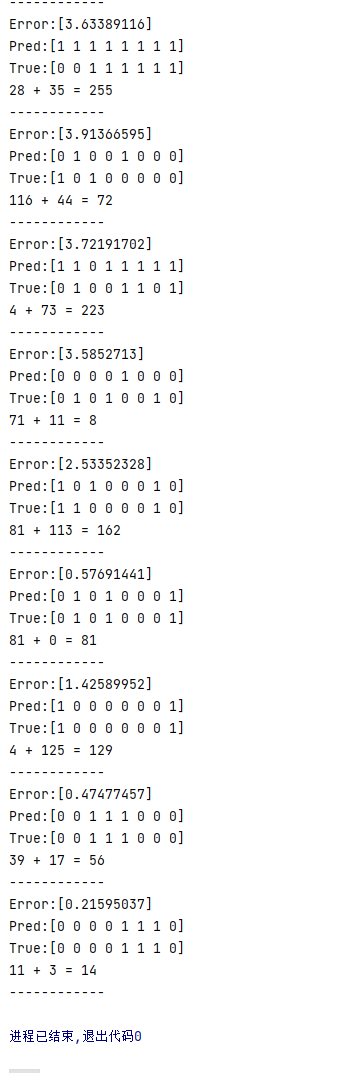
  代码注释给出了很多，可以自行去理解，可以看到，5000次训练以后，就逐渐正确了起来，可以看到RNN训练起来还是很有效的。

5. 实现“Character-Level Language Models”源代码

import numpy as np
import random
#utils.py中定义了本次实验所需要的辅助函数
#包括朴素RNN的前向/反向传播  和我们在上一个实验中实现的差不多
from utils import *
data = open('dinos.txt', 'r').read() #读取dinos.txt中的所有恐龙名字 read()逐字符读取 返回一个字符串
data= data.lower()#把所有名字转为小写
chars = list(set(data))#得到字符列表并去重
print(chars)  #'a'-'z' '\n'  27个字符
data_size, vocab_size = len(data), len(chars)
print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))
char_to_ix = { ch:i for i,ch in enumerate(sorted(chars)) }
ix_to_char = { i:ch for i,ch in enumerate(sorted(chars)) }
print(ix_to_char)

def softmax(x):
    ''''softmax激活函数'''
    e_x = np.exp(x - np.max(x))  # 首先对输入做一个平移 减去最大值 使其最大值为0 再取exp 避免指数爆炸
    return e_x / e_x.sum(axis=0)


def smooth(loss, cur_loss):
    return loss * 0.999 + cur_loss * 0.001


def print_sample(sample_ix, ix_to_char):
    '''
    得到采样的索引对应的字符
    sample_ix:采样字符的索引
    ix_to_char:索引到字符的映射字典
    '''
    txt = ''.join(ix_to_char[ix] for ix in sample_ix)  # 连接成字符串
    txt = txt[0].upper() + txt[1:]  # 首字母大写
    print('%s' % (txt,), end='')


def get_initial_loss(vocab_size, seq_length):
    return -np.log(1.0 / vocab_size) * seq_length


def initialize_parameters(n_a, n_x, n_y):
    """
    用小随机数初始化模型参数

    Returns:
    parameters -- Python字典包含:
                        Wax -- 与输入相乘的权重矩阵, 维度 (n_a, n_x)
                        Waa -- 与之前隐藏状态相乘的权重矩阵, 维度 (n_a, n_a)
                        Wya -- 与当前隐藏状态相乘用于产生输出的权重矩阵, 维度(n_y,n_a)
                        ba --  计算当前隐藏状态的偏置参数  维度 (n_a, 1)
                        by --  计算当前输出的偏置参数  维度 (n_y, 1)
    """
    np.random.seed(1)
    Wax = np.random.randn(n_a, n_x) * 0.01
    Waa = np.random.randn(n_a, n_a) * 0.01
    Wya = np.random.randn(n_y, n_a) * 0.01
    b = np.zeros((n_a, 1))
    by = np.zeros((n_y, 1))

    parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}

    return parameters
### GRADED FUNCTION: clip

def clip(gradients, maxValue):
    '''
    把每个梯度值剪切到 minimum 和 maximum之间.

    Arguments:
    gradients -- Python梯度字典 包含 "dWaa", "dWax", "dWya", "db", "dby"
    maxValue -- 每个大于maxValue或小于-maxValue的梯度值 被设置为该值

    Returns:
    gradients -- Python梯度字典 包含剪切后的切度
    '''

    # 取出梯度字典中存储的梯度
    dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients[
        'dby']

    # 对每个梯度[dWax, dWaa, dWya, db, dby]进行剪切
    for gradient in [dWax, dWaa, dWya, db, dby]:
        # gradient[gradient>maxValue] = maxValue
        # gradient[gradient<-maxValue] = -maxValue
        np.clip(gradient, -maxValue, maxValue, out=gradient)

    gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}

    return gradients


# GRADED FUNCTION: sample

def sample(parameters, char_to_ix, seed):
    """
    根据朴素RNN输出的概率分布对字符序列进行采样

    Arguments:
    parameters --Python字典 包含模型参数 Waa, Wax, Wya, by, and b.
    char_to_ix -- Python字典 把每个字符映射为索引
    seed -- .
    Returns:
    indices -- 包含采样字符索引的列表.
    """

    # 得到模型参数 和相关维度信息
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    vocab_size = by.shape[0]  # 字典大小  输出单元的数量
    n_a = Waa.shape[1]  # 隐藏单元数量

    # Step 1: 创建第一个时间步骤上输入的初始向量 初始化序列生成
    x = np.zeros((vocab_size, 1))
    # Step 1': 初始化a_prev
    a_prev = np.zeros((n_a, 1))

    # 保存生成字符index的列表
    indices = []

    # 检测换行符, 初始化为 -1
    idx = -1

    # 在每个时间步骤上进行循环.在每个时间步骤输出的概率分布上采样一个字符
    # 把采样字典的index添加到indices中. 如果达到50个字符就停止 (说明模型训练有点问题)
    #  用于终止无限循环   模型如果训练的不错的话  在遇到换行符之前不会达到50个字符
    counter = 0
    newline_character = char_to_ix['\n']  # 换行符索引

    while (idx != newline_character and counter != 50):  # 如果生成的字符不是换行符且循环次数小于50  就继续

        # Step 2: 对x进行前向传播   公式(1), (2) and (3)
        a = np.tanh(Wax.dot(x) + Waa.dot(a_prev) + b)  # (n_a,1)
        z = Wya.dot(a) + by  # (n_y,1)
        y = softmax(z)  # (n_y,1)

        np.random.seed(counter + seed)

        # Step 3:从输出的概率分布y中 采样一个字典中的字符索引
        idx = np.random.choice(range(vocab_size), p=y.ravel())
        indices.append(idx)

        # Step 4: 根据采样的索引 得到对应字符的one-hot形式 重写输入x
        x = np.zeros((vocab_size, 1))
        x[idx] = 1

        # 更新a_prev
        a_prev = a

        seed += 1
        counter += 1

    if (counter == 50):
        indices.append(char_to_ix['\n'])

    return indices


def rnn_step_forward(parameters, a_prev, x):
    '''朴素RNN单元的前行传播'''
    # 从参数字典中取出参数
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    # 计算当前时间步骤上的隐藏状态
    a_next = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)
    # 计算当前时间步骤上的预测输出  通过一个输出层(使用softmax激活函数，多分类 ，类别数为字典大小)
    p_t = softmax(np.dot(Wya, a_next) + by)

    return a_next, p_t


def rnn_step_backward(dy, gradients, parameters, x, a, a_prev):
    '''朴素RNN单元的反向传播'''
    gradients['dWya'] += np.dot(dy, a.T)
    gradients['dby'] += dy
    da = np.dot(parameters['Wya'].T, dy) + gradients['da_next']  # backprop into h
    daraw = (1 - a * a) * da  # backprop through tanh nonlinearity
    gradients['db'] += daraw
    gradients['dWax'] += np.dot(daraw, x.T)
    gradients['dWaa'] += np.dot(daraw, a_prev.T)
    gradients['da_next'] = np.dot(parameters['Waa'].T, daraw)
    return gradients


def update_parameters(parameters, gradients, lr):
    '''
    使用随机梯度下降法更新模型参数
    parameters：模型参数字典
    gradients：对模型参数计算的梯度
    lr：学习率
    '''
    parameters['Wax'] += -lr * gradients['dWax']
    parameters['Waa'] += -lr * gradients['dWaa']
    parameters['Wya'] += -lr * gradients['dWya']
    parameters['b'] += -lr * gradients['db']
    parameters['by'] += -lr * gradients['dby']
    return parameters


def rnn_forward(X, Y, a0, parameters, vocab_size=27):
    '''朴素RNN的前行传播
    和上一个实验实验的RNN有所不同，之前我们一次处理m个样本/序列 要求m个序列有相同的长度
    本次实验的RNN，一次只处理一个样本/序列(名字单词) 所以不用统一长度。
     X -- 整数列表，每个数字代表一个字符的索引。 X是一个训练样本 代表一个单词
     Y -- 整数列表，每个数字代表一个字符的索引。 Y是一个训练样本对应的真实标签 为X中的索引左移一位
    '''

    # Initialize x, a and y_hat as empty dictionaries
    x, a, y_hat = {}, {}, {}

    a[-1] = np.copy(a0)

    # initialize your loss to 0
    loss = 0

    for t in range(len(X)):

        # 设置x[t]为one-hot向量形式.
        # 如果 X[t] == None, 设置 x[t]=0向量. 设置第一个时间步骤的输入为0向量
        x[t] = np.zeros((vocab_size, 1))  # 设置每个时间步骤的输入向量
        if (X[t] != None):
            x[t][X[t]] = 1  # one-hot形式 索引位置为1 其余为0

        # 运行一步RNN前向传播
        a[t], y_hat[t] = rnn_step_forward(parameters, a[t - 1], x[t])
        # 得到当前时间步骤的隐藏状态和预测输出

        # 把预测输出和真实标签结合 计算交叉熵损失
        loss -= np.log(y_hat[t][Y[t], 0])

    cache = (y_hat, a, x)

    return loss, cache


def rnn_backward(X, Y, parameters, cache):
    '''朴素RNN的反向传播'''
    # Initialize gradients as an empty dictionary
    gradients = {}

    # Retrieve from cache and parameters
    (y_hat, a, x) = cache
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']

    # each one should be initialized to zeros of the same dimension as its corresponding parameter
    gradients['dWax'], gradients['dWaa'], gradients['dWya'] = np.zeros_like(Wax), np.zeros_like(Waa), np.zeros_like(Wya)
    gradients['db'], gradients['dby'] = np.zeros_like(b), np.zeros_like(by)
    gradients['da_next'] = np.zeros_like(a[0])

    ### START CODE HERE ###
    # Backpropagate through time
    for t in reversed(range(len(X))):
        dy = np.copy(y_hat[t])
        dy[Y[t]] -= 1
        gradients = rnn_step_backward(dy, gradients, parameters, x[t], a[t], a[t - 1])
    ### END CODE HERE ###

    return gradients, a


# GRADED FUNCTION: optimize

def optimize(X, Y, a_prev, parameters, learning_rate=0.01):
    """
    执行一步优化过程(随机梯度下降，一次优化使用一个训练训练).

    Arguments:
    X -- 整数列表，每个数字代表一个字符的索引。 X是一个训练样本 代表一个单词
    Y -- 整数列表，每个数字代表一个字符的索引。 Y是一个训练样本对应的真实标签 为X中的索引左移一位
    a_prev -- 上一个时间步骤产生的隐藏状态
    parameters -- Python字典包含:
                        Wax -- 与输入相乘的权重矩阵, 维度 (n_a, n_x)
                        Waa -- 与之前隐藏状态相乘的权重矩阵, 维度 (n_a, n_a)
                        Wya -- 与当前隐藏状态相乘用于产生输出的权重矩阵, 维度 (n_y, n_a)
                        ba --  计算当前隐藏状态的偏置参数  维度 (n_a, 1)
                        by --  计算当前输出的偏置参数  维度 (n_y, 1)
    learning_rate -- 学习率

    Returns:
    loss -- loss函数值(交叉熵)
    gradients -- python dictionary containing:
                        dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
                        dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
                        dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
                        db -- Gradients of bias vector, of shape (n_a, 1)
                        dby -- Gradients of output bias vector, of shape (n_y, 1)
    a[len(X)-1] -- 最后一个隐藏状态 (n_a, 1)
    """

    # 通过时间前向传播
    loss, cache = rnn_forward(X, Y, a_prev, parameters, vocab_size=27)

    # 通过时间的反向传播
    gradients, a = rnn_backward(X, Y, parameters, cache)

    # 梯度剪切 -5 (min)  5 (max)
    gradients = clip(gradients, maxValue=5)

    # 更新参数
    parameters = update_parameters(parameters, gradients, lr=learning_rate)

    return loss, gradients, a[len(X) - 1]


# GRADED FUNCTION: model

def model(data, ix_to_char, char_to_ix, num_iterations=35000, n_a=50, dino_names=7, vocab_size=27):
    """
    训练模型生成恐龙名字.

    Arguments:
    data -- 文本语料(恐龙名字数据集)
    ix_to_char -- 从索引到字符的映射字典
    char_to_ix -- 从字符到索引的映射字典
    num_iterations -- 随机梯度下降的迭代次数  每次使用一个训练样本(一个名字)
    n_a -- RNN单元中的隐藏单元数
    dino_names -- 采样的恐龙名字数量
    vocab_size -- 字典的大小  文本语料中不同的字符数

    Returns:
    parameters --  训练好的参数
    """

    # 输入特征向量x的维度n_x, 输出预测概率向量的维度n_y  2者都为字典大小
    n_x, n_y = vocab_size, vocab_size

    # 初始化参数
    parameters = initialize_parameters(n_a, n_x, n_y)

    # 初始化loss (this is required because we want to smooth our loss, don't worry about it)
    loss = get_initial_loss(vocab_size, dino_names)

    # 得到所有恐龙名字的列表 (所有训练样本).
    with open("dinos.txt") as f:
        examples = f.readlines()  # 读取所有行 每行是一个名字 作为列表的一个元素
    examples = [x.lower().strip() for x in examples]  # 转换小写 去掉换行符

    # 随机打乱所有恐龙名字 所有训练样本
    np.random.seed(0)
    np.random.shuffle(examples)

    # 初始化隐藏状态为0
    a_prev = np.zeros((n_a, 1))

    # 优化循环
    for j in range(num_iterations):

        # 得到一个训练样本 (X,Y)
        index = j % len(examples)  # 得到随机打乱后的一个名字的索引
        X = [None] + [char_to_ix[ch] for ch in examples[index]]  # 把名字中的每个字符转为对应的索引 第一个字符为None翻译为0向量
        Y = X[1:] + [char_to_ix['\n']]

        # 随机梯度下降 执行一次优化: Forward-prop -> Backward-prop -> Clip -> Update parameters
        # 学习率 0.01
        curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate=0.01)

        # 使用延迟技巧保持loss平稳. 加速训练
        loss = smooth(loss, curr_loss)

        # 每2000次随机梯度下降迭代, 通过sample()生成'n'个字符(1个名字)  来检查模型是否训练正确
        if j % 2000 == 0:

            print('Iteration: %d, Loss: %f' % (j, loss) + '\n')

            seed = 0
            for name in range(dino_names):  # 生成名字的数量

                # 得到采样字符的索引
                sampled_indices = sample(parameters, char_to_ix, seed)
                # 得到索引对应的字符 生成一个名字
                print_sample(sampled_indices, ix_to_char)

                seed += 1  # To get the same result for grading purposed, increment the seed by one.

            print('\n')

    return parameters
parameters = model(data, ix_to_char, char_to_ix) #训练模型

运行结果如下：

['o', 'a', 'u', 'z', 'f', 'l', 'w', 'y', 's', 'x', 'm', 'g', 'j', 'i', 'b', 'v', 'd', 't', 'e', 'p', 'h', 'c', 'n', 'r', 'k', 'q', '\n']
There are 19909 total characters and 27 unique characters in your data.
{0: '\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}
Iteration: 0, Loss: 23.087336

Nkzxwtdmfqoeyhsqwasjkjvu
Kneb
Kzxwtdmfqoeyhsqwasjkjvu
Neb
Zxwtdmfqoeyhsqwasjkjvu
Eb
Xwtdmfqoeyhsqwasjkjvu


Iteration: 2000, Loss: 27.884160

Liusskeomnolxeros
Hmdaairus
Hytroligoraurus
Lecalosapaus
Xusicikoraurus
Abalpsamantisaurus
Tpraneronxeros


Iteration: 4000, Loss: 25.901815

Mivrosaurus
Inee
Ivtroplisaurus
Mbaaisaurus
Wusichisaurus
Cabaselachus
Toraperlethosdarenitochusthiamamumamaon


Iteration: 6000, Loss: 24.608779

Onwusceomosaurus
Lieeaerosaurus
Lxussaurus
Oma
Xusteonosaurus
Eeahosaurus
Toreonosaurus


Iteration: 8000, Loss: 24.070350

Onxusichepriuon
Kilabersaurus
Lutrodon
Omaaerosaurus
Xutrcheps
Edaksoje
Trodiktonus


Iteration: 10000, Loss: 23.844446

Onyusaurus
Klecalosaurus
Lustodon
Ola
Xusodonia
Eeaeosaurus
Troceosaurus


Iteration: 12000, Loss: 23.291971

Onyxosaurus
Kica
Lustrepiosaurus
Olaagrraiansaurus
Yuspangosaurus
Eealosaurus
Trognesaurus


Iteration: 14000, Loss: 23.382338

Meutromodromurus
Inda
Iutroinatorsaurus
Maca
Yusteratoptititan
Ca
Troclosaurus


Iteration: 16000, Loss: 23.265759

Meustoloplohus
Imeda
Iutosaurus
Maca
Yuspanenphurus
Daaisicachtitan
Trodon


Iteration: 18000, Loss: 22.901372

Phytrohaesaurus
Melaaisaurus
Mystoosaurus
Peeamosaurus
Ytronosaurus
Eiakosaurus
Trogonosaurus


Iteration: 20000, Loss: 22.924847

Nixusaurus
Llecalosaurus
Lxusodon
Necalosaurus
Ystrengosaurus
Eg
Trochkosaurus


Iteration: 22000, Loss: 22.759659

Piustolonosaurus
Migbaeron
Myrrocepholus
Peeadosaurus
Yusodomincteros
Eiadosaurus
Trocephods


Iteration: 24000, Loss: 22.695558

Meutosaurus
Incacasaurosbluchesaurus
Jwrosaurus
Mecalosaurus
Yusmanasaurus
Ekagosaurus
Usicheronychus


Iteration: 26000, Loss: 22.697213

Meutrodon
Ingaahus
Itrosaurus
Meeadromaastrumalus
Ytrocenithyptor
Eeberteia
Trochinnhyinntarkicus


Iteration: 28000, Loss: 22.518451

Mevusceratops
Kracaerosaurus
Lwstodoniomunisanosaurus
Ndabasceia
Ystodonosaurus
Eiacosaurus
Trsarisaurus


Iteration: 30000, Loss: 22.503530

Nivusaurus
Jicaaesthaaosaurus
Lustrephus
Ndaadosaurus
Yusmandosaurus
Efagosaurus
Trochisaurus


Iteration: 32000, Loss: 22.237665

Maxusaurus
Jkacalosaurus
Justodon
Macaishalanthuchithedun
Yusianasaurus
Egakosaurus
Trodonathyluskarchasafrushamahaltallang


Iteration: 34000, Loss: 22.426674

Mayusaurus
Ingaagosaurus
Iussqceniravenosaurus
Macaistag
Yrosaurus
Elafosaurus
Trodon

翻译：
Okay, so we have an idea about what RNNs are, why they are super exciting, and how they work. We’ll now ground this in a fun application: We’ll train RNN character-level language models. That is, we’ll give the RNN a huge chunk of text and ask it to model the probability distribution of the next character in the sequence given a sequence of previous characters. This will then allow us to generate new text one character at a time.
好的，我们对RNN是什么已经有了一定的条件，以及为什么他们这么优秀，和他们是怎样工作的，下面我们来围绕一个有趣的应用我们训练RNN模型，我们给RNN一块文章并且询问模型在这句中下个单词的的句子通过上一个字母来判断，这就允许我们每次一个字母形成一个新的文章。
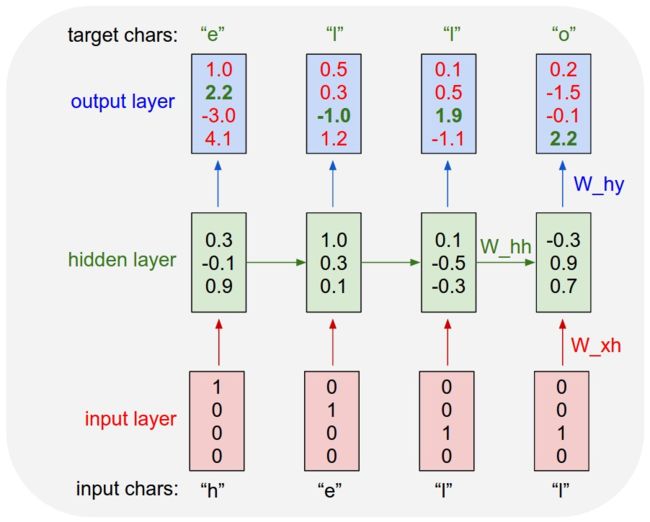
As a working example, suppose we only had a vocabulary of four possible letters “helo”, and wanted to train an RNN on the training sequence “hello”. This training sequence is in fact a source of 4 separate training examples: 1. The probability of “e” should be likely given the context of “h”, 2. “l” should be likely in the context of “he”, 3. “l” should also be likely given the context of “hel”, and finally 4. “o” should be likely given the context of “hell”.
我们举一个例子，我们有一个单词是helo，并且想要训练一个RNN模型寻连hello，这个训练的序列是由四个单独的训练例子担任的，第一个字母e应该由h来给出，l应该由he来给出，l应该由hel来给出，最后一个o应该由hell给出。
Concretely, we will encode each character into a vector using 1-of-k encoding (i.e. all zero except for a single one at the index of the character in the vocabulary), and feed them into the RNN one at a time with the step function. We will then observe a sequence of 4-dimensional output vectors (one dimension per character), which we interpret as the confidence the RNN currently assigns to each character coming next in the sequence.
我们将每个字母进行独热编码（每个向量只有一个为1，其余为0，并且用RNN对每一步进行训练，我们将会观测出一个四个维度的输出向量代表每个字母)，我们用RNN去判断出每个字母。如下图所示。

7. “编码器-解码器”的简单实现

 完整代码如下：

# code by Tae Hwan Jung(Jeff Jung) @graykode, modify by wmathor
import torch
import numpy as np
import torch.nn as nn
import torch.utils.data as Data

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# S: Symbol that shows starting of decoding input
# E: Symbol that shows starting of decoding output
# ?: Symbol that will fill in blank sequence if current batch data size is short than n_step

letter = [c for c in 'SE?abcdefghijklmnopqrstuvwxyz']
letter2idx = {n: i for i, n in enumerate(letter)}

seq_data = [['man', 'women'], ['black', 'white'], ['king', 'queen'], ['girl', 'boy'], ['up', 'down'], ['high', 'low']]

# Seq2Seq Parameter
n_step = max([max(len(i), len(j)) for i, j in seq_data]) # max_len(=5)
n_hidden = 128
n_class = len(letter2idx) # classfication problem
batch_size = 3

def make_data(seq_data):
    enc_input_all, dec_input_all, dec_output_all = [], [], []

    for seq in seq_data:
        for i in range(2):
            seq[i] = seq[i] + '?' * (n_step - len(seq[i])) # 'man??', 'women'

        enc_input = [letter2idx[n] for n in (seq[0] + 'E')] # ['m', 'a', 'n', '?', '?', 'E']
        dec_input = [letter2idx[n] for n in ('S' + seq[1])] # ['S', 'w', 'o', 'm', 'e', 'n']
        dec_output = [letter2idx[n] for n in (seq[1] + 'E')] # ['w', 'o', 'm', 'e', 'n', 'E']

        enc_input_all.append(np.eye(n_class)[enc_input])
        dec_input_all.append(np.eye(n_class)[dec_input])
        dec_output_all.append(dec_output) # not one-hot

    # make tensor
    return torch.Tensor(enc_input_all), torch.Tensor(dec_input_all), torch.LongTensor(dec_output_all)

'''
enc_input_all: [6, n_step+1 (because of 'E'), n_class]
dec_input_all: [6, n_step+1 (because of 'S'), n_class]
dec_output_all: [6, n_step+1 (because of 'E')]
'''
enc_input_all, dec_input_all, dec_output_all = make_data(seq_data)

class TranslateDataSet(Data.Dataset):
    def __init__(self, enc_input_all, dec_input_all, dec_output_all):
        self.enc_input_all = enc_input_all
        self.dec_input_all = dec_input_all
        self.dec_output_all = dec_output_all
    
    def __len__(self): # return dataset size
        return len(self.enc_input_all)
    
    def __getitem__(self, idx):
        return self.enc_input_all[idx], self.dec_input_all[idx], self.dec_output_all[idx]

loader = Data.DataLoader(TranslateDataSet(enc_input_all, dec_input_all, dec_output_all), batch_size, True)

# Model
class Seq2Seq(nn.Module):
    def __init__(self):
        super(Seq2Seq, self).__init__()
        self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
        self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
        self.fc = nn.Linear(n_hidden, n_class)

    def forward(self, enc_input, enc_hidden, dec_input):
        # enc_input(=input_batch): [batch_size, n_step+1, n_class]
        # dec_inpu(=output_batch): [batch_size, n_step+1, n_class]
        enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
        dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]

        # h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
        _, h_t = self.encoder(enc_input, enc_hidden)
        # outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
        outputs, _ = self.decoder(dec_input, h_t)

        model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
        return model

model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

for epoch in range(5000):
  for enc_input_batch, dec_input_batch, dec_output_batch in loader:
      # make hidden shape [num_layers * num_directions, batch_size, n_hidden]
      h_0 = torch.zeros(1, batch_size, n_hidden).to(device)

      (enc_input_batch, dec_intput_batch, dec_output_batch) = (enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
      # enc_input_batch : [batch_size, n_step+1, n_class]
      # dec_intput_batch : [batch_size, n_step+1, n_class]
      # dec_output_batch : [batch_size, n_step+1], not one-hot
      pred = model(enc_input_batch, h_0, dec_intput_batch)
      # pred : [n_step+1, batch_size, n_class]
      pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
      loss = 0
      for i in range(len(dec_output_batch)):
          # pred[i] : [n_step+1, n_class]
          # dec_output_batch[i] : [n_step+1]
          loss += criterion(pred[i], dec_output_batch[i])
      if (epoch + 1) % 1000 == 0:
          print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
          
      optimizer.zero_grad()
      loss.backward()
      optimizer.step()
    
# Test
def translate(word):
    enc_input, dec_input, _ = make_data([[word, '?' * n_step]])
    enc_input, dec_input = enc_input.to(device), dec_input.to(device)
    # make hidden shape [num_layers * num_directions, batch_size, n_hidden]
    hidden = torch.zeros(1, 1, n_hidden).to(device)
    output = model(enc_input, hidden, dec_input)
    # output : [n_step+1, batch_size, n_class]

    predict = output.data.max(2, keepdim=True)[1] # select n_class dimension
    decoded = [letter[i] for i in predict]
    translated = ''.join(decoded[:decoded.index('E')])

    return translated.replace('?', '')

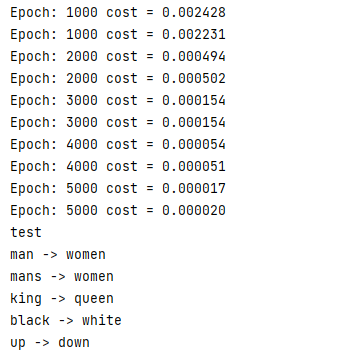
print('test')
print('man ->', translate('man'))
print('mans ->', translate('mans'))
print('king ->', translate('king'))
print('black ->', translate('black'))
print('up ->', translate('up'))

 运行结果如图：

参考文献

https://blog.csdn.net/ABU366/article/details/127824295?spm=1001.2014.3001.5502

http://karpathy.github.io/2015/05/21/rnn-effectiveness/