二分类器的常用评价指标
所谓分类器,就是一种处理分类任务的模型。这个模型既可以是人工设定的某些规则的集合,也可以是通过机器学习得到的分类模型,根据类别多少,有二分类器和多分类器之别。
有一些比较经典的应用场景,比如说:
短视频、新闻、广告等个性化推荐;
投资、借贷等涉及到的风险管理场景;
垃圾邮件、垃圾短信的识别;
图像识别等
那问题来了,怎么能够判断某分类器是否可以胜任一个业务场景,又如何比较分类器之间的优劣呢,这就引出本文要讨论的6种分类指标了。
不过,在介绍分类指标之前,我们先引入一个重要概念——混淆矩阵。
混淆矩阵
所谓混淆矩阵,就是记录分类结果的一张表格的矩阵表示,在二分类场景里是一个2x2的矩阵。如下图。

TP(True Positive):真正例,实际上和预测中都是正例;
FP(False Positive):假正例,实际上是负例,但是被预测为正例了;
FN(False Negative):假负例,实际上是正例,但是被预测为负例了;
TN(True Negative):真负例,实际上和预测中都是负例。
上述四种情况定义了二分类器的所有分类结果,我们接下来介绍的所有指标,都基于这四种基本情况。
常用指标汇总
| 计算方法 | 关注点 | 缺陷 | |
|---|---|---|---|
| Accuracy | T P + T N T P + F P + T N + F N \frac{TP+TN}{TP+FP+TN+FN} TP+FP+TN+FNTP+TN | 预测正确的概率 | 无法数据不平衡的情况下使用 |
| Precision | T P T P + F P \frac{TP}{TP+FP} TP+FPTP | 预测正例也是实际正例的概率 | 无法单独使用 |
| Recall | T P T P + F N \frac{TP}{TP+FN} TP+FNTP | 实际正例也是预测正例的概率 | 无法单独使用 |
| F1 | 2 × P R P + R \frac{2\times PR}{P+R} P+R2×PR | PR值的调和平均 | 无法反映排序情况 |
| ROC-AUC | ROC与坐标轴围成的面积 | 提高召回率R的代价 | 极端不平衡时数值会膨胀到失去分辨能力 |
| PR-AUC | PR曲线与坐标轴围成的面积 | 综合考虑PR值 | 不好看 :) |
我们直接把缺陷列在了表格的最后一列,下面我们通过一个简单的例子说明之。
举例:杀人游戏
现有12个人参与一场“杀人游戏”,设有好人9人,杀手3人。杀手势力每晚可以杀一个人,所有人白天可以投票驱逐一个人,被杀者和被驱逐者视为被淘汰,当场上只有一方势力时,游戏结束。
没有参考价值的指标 acc、p、r
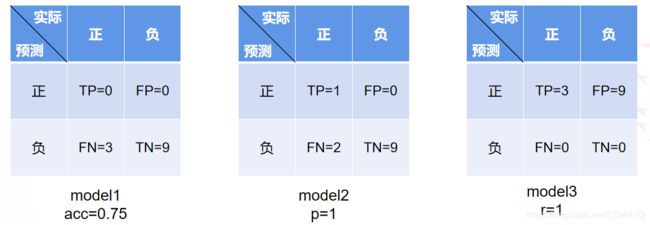
现在参与者们捡到了三个分类器,我们记为model1、model2和model3,分别用acc、p和r标明了性能,乍一看都很不错:
- model1 : acc=0.75
model2 : p=1
model3 : r=1
- 对于model1,只需要把所有人都判作平民,就可保证 75% 的 acc 性能;
- 对于model2,只需要蒙对一个杀手,其他都判做平民,就可保证 p 值为 1;
- 对于model3,只需要把所有人都判作杀手,就可保证 100% 的召回率
显然,三个模型唯有 model2 对局面有所贡献,其他两者的分类结果都有可能毫无意义,并且连 model2 也可能只找到 1/3 的杀手,作用有限。因此,上述三种指标可以说是没有参考价值的指标。
究其关键,一是数据不平衡的情况下,acc 指标确实没有参考意义;二是只关注 p 值可能造成大量漏网之鱼,只关注 r 值又可能产生毫无意义的分类结果。顺理成章的,一种关注 PR 平均性能的指标 F1 值出现了。但我们要说,F1 值虽可以大致描述模型性能,但在一些注重排序的业务场景下,仍可能没有比较价值。
没有比较价值的指标 F1
参与者们放弃了上述三个模型,幸运地又找到了三个新模型,我们记为 model4, model5 和 model6。它们都用 P、R 和 F1 值标注了性能表现,并且为了提高容错率、尽可能多的找出杀手,三个模型都将6人判作为杀手,它们的 P 值都等于 0.5 ,R 值都等于 1 ,F1 值也都等于 0.75。由于误判了三个好人,三个模型还输出了每个预测正例的概率。
有平民认为,即使 F1 值都等于 0.75,这三个模型之间的差异仍有可能非常巨大,比如说下图这种情况。

- model4 预测概率前三的样本都是误判样本
- model5 预测概率前三的样本有两个是误判样本
- model6 前三只有一个误判样本
model4~6 之间的区别如此之大——如果选择 model4 策略一定会输,model5 赢的惊险, model6 则轻松搞定——让人难以想象三个模型的 F1 值都是 0.75。
造成这种情况的主要原因是参与者们选择按照预测概率大小进行决策,如果他们选择直接投骰子决定归票人选,那这三个模型确实没有差异。
可是,人们总是排斥不确定性的。
从一种名叫ROC(受试者操作曲线)的图形就可以看出不同模型输出结果顺序的好坏。
ROC的绘制
介绍ROC之前,我们得介绍两个新的指标,TPR和FPR。
| 计算方法 | 关注点 | |
|---|---|---|
| TPR(True Positive Rate) | T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP | 即召回率 |
| FPR(False Positive Rate) | F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP | 预测正例不是实际正例的概率 |
我们之前介绍的 4 个指标都先验地确定了正例和负例地分类阈值,TP、FP、TN和FN的数量也是固定的,但是 ROC 和后文介绍的 PR 值则不然,它没有预定的分类阈值,而是让阈值在 [0,1] 上滑动,每次滑动都记录一次 TPR 和 FPR,最后再把两个序列的相关信息制成图表。
正如图中所绘,ROC 图以 FPR 为横轴,以 TPR 为纵轴。当分类阈值为1时,所有样本都被判作负例,TP和FP、TPR和FPR都为0;当分类阈值为0时,所有样本都被判作正例,FN和TN都为0,TPR和FPR都为1。
ROC 可以直观地显示三个模型的优劣,与 F1 值相比,它对性能的展现增加了两个维度,一个是滑动阈值下的整体性能,另一个是分类结果的排序好坏。后者可以说是前者的延申。
我们之前讲到 ROC 的关注点是提高召回率的代价,召回率就是ROC的TPR,而这个代价的直观体现就是ROC的斜率,当斜率较大时,TPR向上提高只会造成FPR向右移动较小的量,而斜率减小时,FPR向右移动的量就会相应增加,模型必须作出更多误判才能使召回率得到提高。
由于我们无法直接量化比较两条曲线,通常用ROC-AUC(ROC-Area Under Curve,ROC下面积)代替ROC图进行比较,越大越好。
虽然说 ROC 不关心实际正例和实际负例的数量关系,并因此被很多人认为能很好地衡量模型在数据不平衡情况下的性能,但其实不然,实践上,ROC容易数值膨胀的特点让其无法很好地衡量模型的优劣,我们仍然举例说明。
当平民人数到达900人时。。。
我们以 model4 为例,使 model4 的 TPR 上升到 1 的代价是错判 3 个好人,即:
- 当好人只有 9 人时,FPR 代价为: F P R = F P F P + T N = 3 3 + 6 = 0.33 FPR=\frac{FP}{FP+TN}=\frac{3}{3+6}=0.33 FPR=FP+TNFP=3+63=0.33
- 而当好人变成 900 人时,FPR 代价为: F P R = F P F P + T N = 3 3 + 897 = 0.0033 FPR=\frac{FP}{FP+TN}=\frac{3}{3+897}=0.0033 FPR=FP+TNFP=3+8973=0.0033
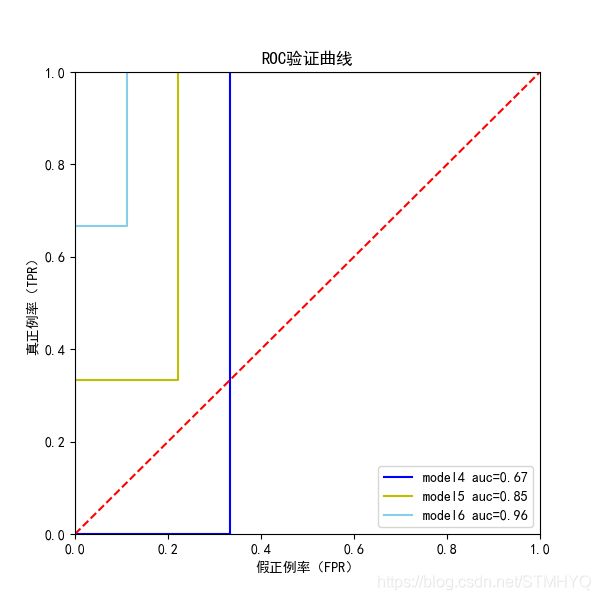
这个区别反映到图像上,如图。

通常来讲,我们描述数据的精度是小数点后两位,这个精度下 model4~6 的性能是相同的,ROC曲线彻底失去分辨能力。
我们应该使用PR曲线(900平民)
与 ROC 的绘制方法类似,只不过这次我们记录的是每个阈值的 P 和 R 值,制成曲线图后是这样的。
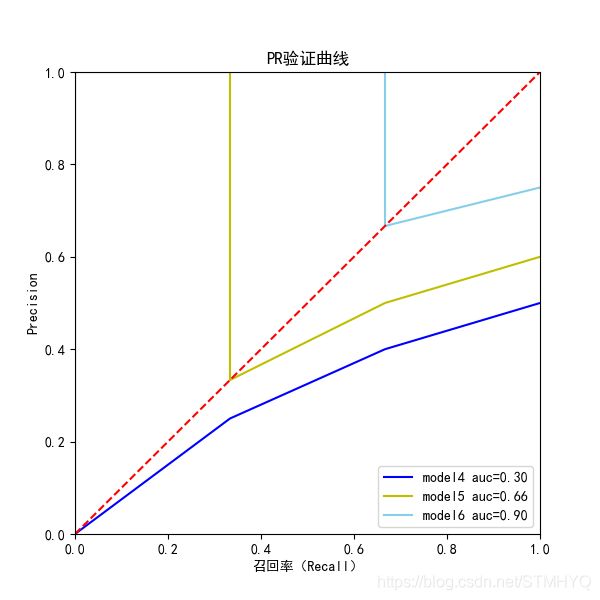
同样是 900 平民 3 杀手的配置,PR 曲线完美地区分开了三个模型的性能表现。可以说,PR 曲线在数据极度不平衡的情况下依然保持了良好的分辨能力和参考意义。
总结
本篇博文主要针对的是二分类器,且由于经验所限,也只列出了一些最常用最经典的评价,另有其他指标如 KS、 F β F\beta Fβ等没有涉及,期待有其他同学予以补充。
虽说评价指标之间却有全面和局部、对数据不平衡敏感和不敏感之别,但是希望诸位读者和我自己都不要孤立和教条地看待和选择指标,不同的业务场景、不同的目的有不同的要求,运用智慧和经验灵活运用才是我们所追求的境界。
最后,用个表格总结一下本文介绍的指标吧。
| 应用场景 | |
|---|---|
| Accuracy | 数据平衡,注重所有类别的分类情况 |
| Precision | 和Recall一起用,当误判造成的损失较大时。例如垃圾邮件 |
| Recall | 和Precision一起用,当遗漏造成的损失较大时。例如违约预测 |
| F1 | 不注重排序的业务场景,只关注正例的分类情况。例如广告点击预测 |
| ROC-AUC | 数据不平衡情况没有非常严重,同时注重两种类别的分类情况 |
| PR-AUC | 只关注正例的分类情况 |
参考文献
[1] Davis J . The Relationship Between Precision-Recall and ROC Curves[C]// Proceedings of the 23th International Conference on Machine Learning, 2006. 2006.