pytorch中的NLLLoss和CrossEntropy
直接计算CrossEntropy
import torch
import torch.nn.functional as F
先按照流程手动计算CrossEntropy
class_dim = 3
z = torch.Tensor([[3, 1, -3]])
z
tensor([[ 3., 1., -3.]])
y = torch.nn.Softmax(dim=1)(z)
y
tensor([[0.8789, 0.1189, 0.0022]])
注意:交叉熵在信息论中log是以2为底,在pytorch中log是以e为底
计算CrossEntropy过程,图片来自这里
y_log = torch.log(y)
y_log
tensor([[-0.1291, -2.1291, -6.1291]])
y_hat = torch.tensor([1], dtype=int)
y_hat
tensor([1])
y_1_hot = torch.nn.functional.one_hot(y_hat, class_dim)
y_1_hot
tensor([[0, 1, 0]])
l = torch.tensor(0, dtype=torch.float32)
for y_log_, y_1_hot_ in zip(y_log, y_1_hot):
l += torch.dot(-y_log_.to(torch.float32), y_1_hot_.to(torch.float32))
l = torch.div(l, len(y_log))
l
tensor(2.1291)
最终对多笔数据求的是平均交叉熵
NLLLoss
The negative log likelihood loss.
def nll_loss(y_log, y_hat):
y_1_hot = torch.nn.functional.one_hot(y_hat, class_dim)
l = torch.tensor(0, dtype=torch.float32)
for y_log_, y_1_hot_ in zip(y_log, y_1_hot):
l += torch.dot(-y_log_.to(torch.float32), y_1_hot_.to(torch.float32))
l = torch.div(l, len(y_log))
return l
F.nll_loss(y_log, y_hat)
tensor(2.1291)
nll_loss(y_log, y_hat)
tensor(2.1291)
可以发现,nll_loss输入为经过了softmax和log后值,nll_loss所做的操作就是对y_log取负号,然后对y_index进行one hot编码,最后取真实类标位置上的-y_log值,即体现在点乘上
CrossEntropyLoss
def cross_entropy(z, y_hat):
y = torch.nn.Softmax(dim=1)(z)
y_log = torch.log(y)
return nll_loss(y_log, y_hat)
F.cross_entropy(z, y_hat)
tensor(2.1291)
cross_entropy(z, y_hat)
tensor(2.1291)
可以发现,cross_entropy输入是未经过softmax和log后值,cross_entropy所做的操作就是对y进行softmax和取log,最后对y_log进行nll_loss
往往数据不会只有1笔,由于计算过程已经对多笔数据支持,所以只需在输入数据上增加
class_dim = 3
data_num = 5
z = torch.randn(data_num, class_dim)
y_hat = torch.ones(data_num, dtype=int).random_(class_dim)
z, y_hat
(tensor([[ 0.2319, 0.2875, -0.2994],
[ 0.7351, -1.3286, -0.4470],
[ 0.9836, -0.5633, -0.3552],
[ 0.8043, -0.3892, 1.2848],
[ 0.9196, 2.2589, -1.3184]]),
tensor([2, 0, 2, 1, 1]))
cross_entropy(z, y_hat)
tensor(1.2223)
F.cross_entropy(z, y_hat)
tensor(1.2223)
CrossEntropy
上面计算过程有个疑问,就是交叉熵为什么要这么求?
首先需要理解交叉熵含义,可以查看这个知乎回答加以理解,简单来说,交叉熵损失核心是熵的计算。所以有取log运算和取负号,而 − l n x -lnx −lnx函数长这样:
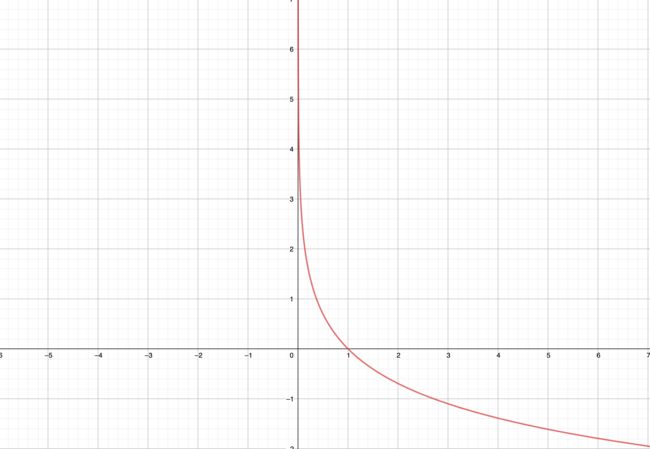
可以发现经过softmax函数后的值域为[0,1],很好的满足了 − l n x -lnx −lnx取值范围。上图也很好体现了信息量关系:概率越小,信息量越大。而信息熵是同分布下信息量在其概率下的期望。
交叉熵求的是非真实分布的信息量在真实分布概率下期望:
∑ k = 1 N p k log 2 1 q k \sum_{k=1}^{N} p_{k} \log _{2} \frac{1}{q_{k}} k=1∑Npklog2qk1
或者是机器学习中常用表示(e为低,取负号)
∑ k = 1 N − p k ln q k \sum_{k=1}^{N} -p_{k} \ln {q_{k}} k=1∑N−pklnqk
其中 p k p_{k} pk 表示真实分布, q k \quad q_{k} qk 表示非真实分布(预测分布)。
交叉熵在非真实分布与真实分布一样时取得最小。怎么样更好解释这个结论暂时没找到。
那么为什么要求交叉熵最小呢?
实践上我们求的相对熵(KL散度)要最小,即真实分布和非真实分布差异,只是其中的真实分布的信息熵我们已经知道,求相对熵最小即求交叉熵最小。

