matlab编写程序实现dft和fft算法（不使用matlab自带的函数）

matlab编写程序实现dft和fft算法（不使用matlab自带的函数）
一、dft算法
利用dft的定义公式，进行程序设计

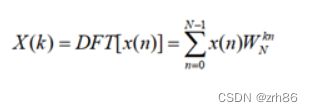
其中WN=exp(-j2pi/N)
二、fft算法
fft作为dft的一种快速算法，主要利用旋转因子的特性(周期性、对称性、可约性)，把长序列的dft分解为几个短序列的dft。
以基2dit-fft为例，计算N=2^M 点的dft，要进行M级运算，每级有N/2个蝶形运算。
第L级运算的蝶形节点的间距为2^(L-1)。
L=1：M
J=0：2^(L-1)-1
旋转因子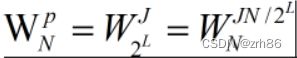
程序框图

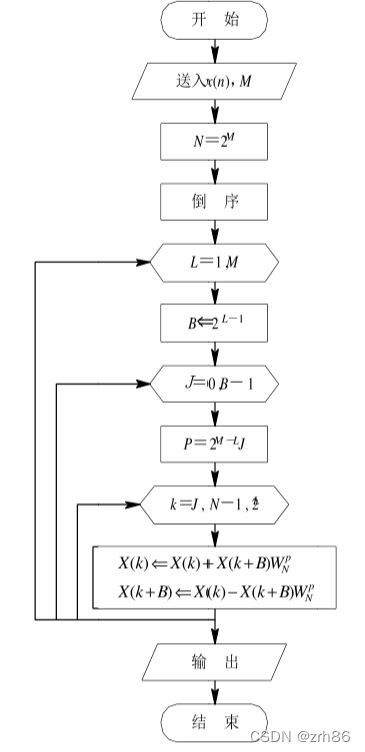
三、算法实现
1.dft(定义法)代码：

tic;%dft的matlab程序
clc;
clear all;
close all;
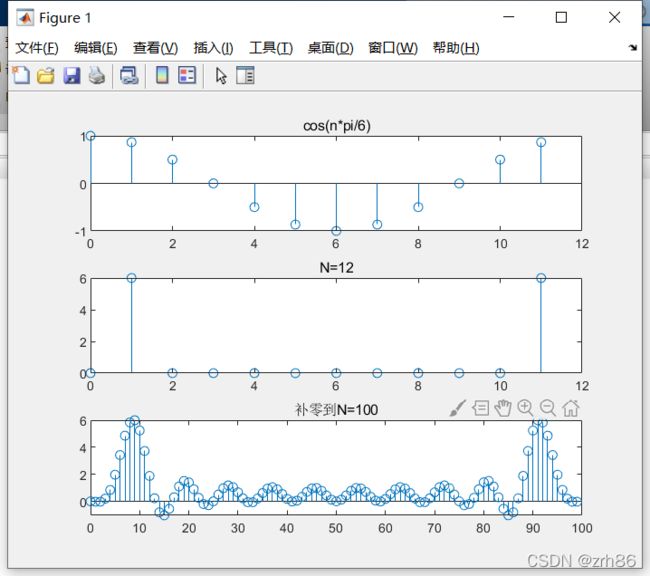
N=12;
n=0:N-1;
k=0:N-1;
xn=cos(n*pi/6);
subplot(3,1,1);
stem(n,xn);title('cos(n*pi/6)');
W=exp(-j*2*pi/N);
kn=n'*k;
Xk=xn*(W.^kn);
subplot(3,1,2);
stem(n,Xk);title('N=12');

N=100;
n=0:N-1;
k=0:N-1;
xn=cos(n*pi/6);
xn=[xn(1:1:12),zeros(1,N-12)];%补零到N个
W=exp(-j*2*pi/N);
kn=n'*k;
Xk=xn*(W.^kn);
subplot(3,1,3);
stem(n,Xk);title('补零到N=100');

toc;
%补零后，其实是对DFT结果做了插值，克服栅栏效应，使谱外观平滑化

2.把dft封装成函数，再调用

function [X]=dft_di(xn,N)
n=0:N-1;
k=0:N-1;
W=exp(-j*2*pi/N);
kn=n'*k;
X=xn*(W.^kn);
end

调用：

clc;clear all;close all;
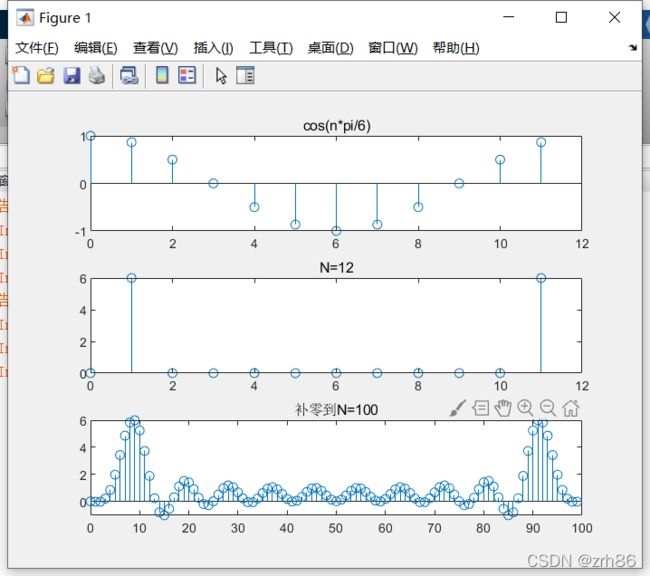
N=12;
n=0:N-1;
k=0:N-1;
xn=cos(n*pi/6);
subplot(3,1,1);
stem(n,xn);title('cos(n*pi/6)');
Xk=dft_di(xn,N);
subplot(3,1,2);
stem(k,Xk);title('N=12');

N=100;
n=0:N-1;
k=0:N-1;
xn=cos(n*pi/6);
xn=[xn(1:1:12),zeros(1,N-12)];
Xk=dft_di(xn,N);
subplot(3,1,3);
stem(k,Xk);title('补零到N=100');

%补零后，其实是对DFT结果做了插值，克服栅栏效应，使谱外观平滑化

3.fft代码：

function [Xk]=fft_j2(xn)
M=nextpow2(length(xn));
N=2^M;

if length(xn)<N;
    xn=[xn,zeros(1,N-length(xn))];
end
n=1:N;
x=xn(bitrevorder(n-1)+1);
for m=0:N/2-1;
    W(m+1)=exp(-j*2*pi/N)^m;
end
for L=1:M;
    B=2^(L-1);
    for J=0:B-1;
        P=2^(M-L)*J;
        for K=J:2^L:N-2;
            T=x(K+1)+x(K+B+1)*W(P+1);
            x(K+B+1)=x(K+1)-x(K+B+1)*W(P+1);
            x(K+1)=T;
        end
    end
end
Xk=x;
        

function y=myditfft(xn)
M=nextpow2(length(xn));
N=2^M;


if length(xn)<N;
    xn=[xn,zeros(1,N-length(xn))];
end
for m=0:N/2-1
    WN(m+1)=exp(-j*2*pi/N)^m;
end


J=0;
for I=0:N-1;
    if I<J;
        T=xn(I+1);xn(I+1)=xn(J+1);xn(J+1)=T;
    end
    K=N/2;
    while J>=K;
        J=J-K;K=K/2;
    end
    J=J+K;
end


for L=1:M;
    B=2^(L-1);
    for R=0:B-1;
        P=2^(M-L)*R;
        for K=R:2^L:N-2;
            T=xn(K+1)+xn(K+B+1)*WN(P+1);
            xn(K+B+1)=xn(K+1)-xn(K+B+1)*WN(P+1);
            xn(K+1)=T;
        end
    end
    
end
y=xn
    
    

以上两个fft的函数不同之处在于倒序的程序方法不同。
调用：

clc;clear all;close all;
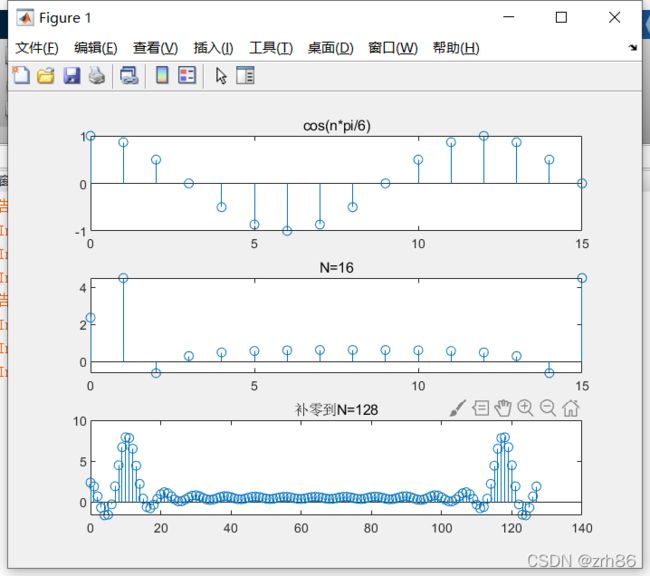
N=16;
n=0:N-1;
k=0:N-1;
xn=cos(n*pi/6);
subplot(3,1,1);
stem(n,xn);title('cos(n*pi/6)');
Xk=fft_j2(xn);
subplot(3,1,2);
stem(k,Xk);title('N=16');

N=128;
n=0:N-1;
k=0:N-1;
xn=cos(n*pi/6);
xn=[xn(1:1:16),zeros(1,N-16)];
Xk=fft_j2(xn);
subplot(3,1,3);
stem(k,Xk);title('补零到N=128');

%补零后，其实是对DFT结果做了插值，克服栅栏效应，使谱外观平滑化

另附有结果图：
dft的：

封装调用dft的：

fft的：

另外附有其他参考
添加链接描述

添加链接描述