R语言:glmnet包重点详解及多类回归实现(lasso/岭回归/弹性网)
文章目录
-
-
-
-
-
- 1.1 Glmnet介绍
- 1.2 Glmnet数学表示
- 1.3 Glmnet多回归方式对比
- 1.4 Glmnet代码原理
- 1.5 Glmnet安装与载入
- 1.6 Glmnet回归使用
- 1.7 Glmnet回归结果分析
- 1.8 Glmnet回归结果可视化
- 1.9 Glmnet模型评价方法
- 1.10 Glmnet选择最佳模型
- 1.11 Glmnet预测
-
-
-
-
1.1 Glmnet介绍
Glmnet是一个通过惩罚极大似然来适应广义线性和相似模型的软件包。控制在对数尺度上计算lasso回归或弹性网回归的参数为正则化参数lambda。该算法速度非常快,并且可以利用输入矩阵x的稀疏性。
它适合线性、logistic和多项式、泊松等回归模型。它还可以拟合多元线性回归模型、定制族广义线性回归模型和lasso回归模型,在该软件包中还拥有预测、绘图、交叉验证的方法。
1.2 Glmnet数学表示
Glmnet主要解决的问题是:
m i n β 0 , β 1 N ∑ i = 1 N w i l ( y i , β 0 + β T x i ) + λ [ ( 1 − α ) ∣ ∣ β ∣ ∣ 2 2 / 2 + α ∣ ∣ β ∣ ∣ 1 ] min_{\beta_0,\beta}\frac{1}{N}\sum_{i=1}^{N}w_{i}l(y_{i},\beta_0+\beta^{T}x_{i})+\lambda [(1-\alpha )||\beta ||_{2}^{2}/2+\alpha ||\beta ||_{1}] minβ0,βN1i=1∑Nwil(yi,β0+βTxi)+λ[(1−α)∣∣β∣∣22/2+α∣∣β∣∣1]
在λ值的网格上覆盖整个可能的解的范围。这里l(yi,ηi)函数是观测值i的负对数似然估计,例如,高斯情况下,它是12*(yi−ηi)2。
1.3 Glmnet多回归方式对比
弹性网回归由α进行控制,弥补了lasso回归(α=1,默认值)和岭回归(α=0)之间的差距。参数λ控制了惩罚的整体强度。
| α | 回归 |
|---|---|
| α=1,默认值 | lasso回归 |
| α=0 | ridge 岭回归 |
| α=(0,1) | 弹性网回归 |
众所周知,ridge回归缩小了相互关联的预测因子的系数,而lasso回归倾向于选择其中一些而丢弃其他的,即lasso回归拥有选择变量的作用。
弹性网回归融合了这两者的优缺点:如果预测因子在组中相关,α=0.5倾向于选择或忽略整个组的特征。这是一个更高级别的参数,用户可能预先选择一个α值或尝试几个不同的α值。函数中α参数的一个用途是求数值稳定性;例如,当α更加接近1时,弹性网会更加与lasso回归相似,但消除了极端数据使得模型过于简单的情况。
1.4 Glmnet代码原理
glmnet算法采用循环坐标下降法,在其他参数不变的情况下,依次优化目标函数,并重复循环,直到收敛。该R包还利用强规则对活动集进行有效约束。由于高效的更新和技术,如热启动和活动集收敛,该算法可以非常快速地计算。
该代码可以处理稀疏的输入矩阵格式,以及系数的范围限制。glmnet的核心代码是一组Fortran子程序,这使得其执行速度非常快。
1.5 Glmnet安装与载入
如其他所有R包相似,安装glmnet只需要一行代码。
install.packages("glmnet")
在R Studio中设置为国内的镜像网站 能够加快包的安装速度。
library(glmnet)
1.6 Glmnet回归使用
载入R自带的数据包来进行Glmnet的展示
data("MultinomialExample")
在我们不调整参数的默认情况下,它使用的是高斯分布或者说最小二乘来进行回归。首先确定需要使用的回归方法,
而我们首先需要确定使用的回归方法
如Lasso回归、Ridge回归、Elastic net等。
fit = glmnet(data_x, data_y,alpha =0.5,standardize=TRUE)
alpha=0 岭回归 不进行变量的选择
alpha=1 lasso回归 进行变量的选择
其他[0,1]间取值则是Elastic net回归。
fit = glmnet(MultinomialExample$x,MultinomialExample$y,alpha = 0.5,standardize=TRUE)
standardize进行标准化 避免量纲影响。
Fit是glmnet类的一个对象,它包含适合模型的所有相关信息,以供进一步使用。不必直接使用该对象进行分析。在Glmnet包中对fit对象提供了各种方法,如plot, print, coef和predict,使我们能够更高效地执行这些任务。
1.7 Glmnet回归结果分析
打印拟合结果
print(fit)
> #打印拟合结果
> print(fit)
Call: glmnet(x = MultinomialExample$x, y = MultinomialExample$y, alpha = 0, standardize = TRUE)
Df %Dev Lambda
1 30 0.00 267.300
2 30 0.28 243.600
3 30 0.30 221.900
4 30 0.33 202.200
5 30 0.37 184.200
6 30 0.40 167.900
7 30 0.44 153.000
8 30 0.48 139.400
9 30 0.53 127.000
10 30 0.58 115.700
11 30 0.64 105.400
12 30 0.70 96.060
13 30 0.76 87.530
14 30 0.84 79.750
15 30 0.92 72.670
16 30 1.00 66.210
17 30 1.10 60.330
18 30 1.20 54.970
19 30 1.32 50.090
20 30 1.44 45.640
21 30 1.58 41.580
22 30 1.73 37.890
23 30 1.89 34.520
24 30 2.07 31.460
25 30 2.26 28.660
26 30 2.47 26.120
27 30 2.69 23.800
28 30 2.94 21.680
29 30 3.21 19.760
30 30 3.50 18.000
31 30 3.81 16.400
32 30 4.15 14.940
33 30 4.52 13.620
34 30 4.92 12.410
35 30 5.34 11.300
36 30 5.80 10.300
37 30 6.29 9.385
38 30 6.82 8.552
39 30 7.38 7.792
40 30 7.98 7.100
41 30 8.62 6.469
42 30 9.29 5.894
43 30 10.01 5.371
44 30 10.76 4.893
45 30 11.55 4.459
46 30 12.38 4.063
47 30 13.25 3.702
48 30 14.15 3.373
49 30 15.08 3.073
50 30 16.04 2.800
- 它从左到右显示非零系数的数量(Df),解释的百分比(null)偏差(%Dev)和λ的值(Lambda)。
- glmnet在默认情况下会拟合100个lambda值的模型。
- 如果%Dev没有从一个lambda到下一个lambda进行足够大小的更改,它会认为拟合已经完成,提前停止,以提高计算速度。
- 为了简洁起见,我们在这里截断了打印结果,只展示了部分。
1.8 Glmnet回归结果可视化
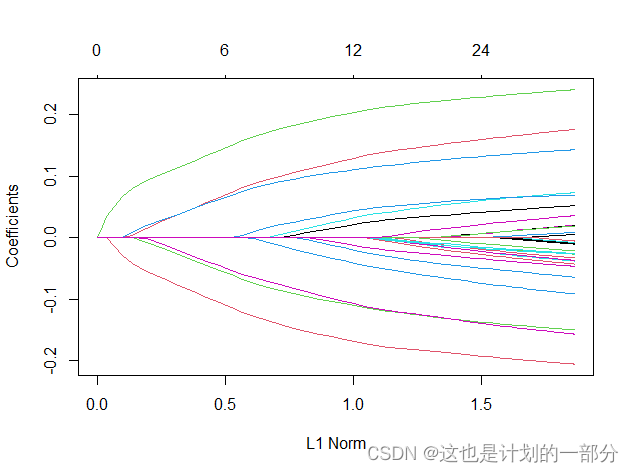
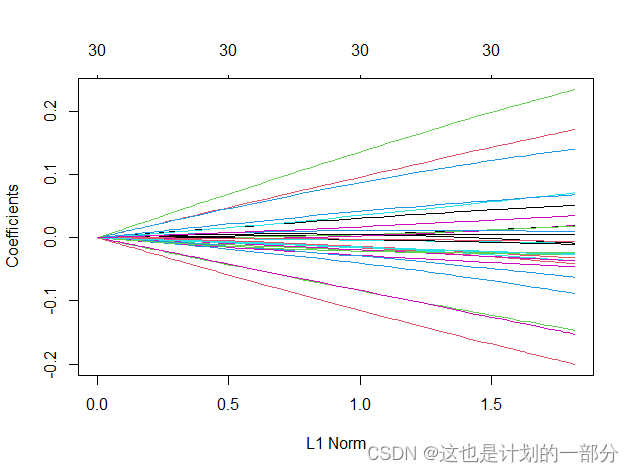
我们可以通过plot()来可视化回归结果
plot(fit)
弹性网:
lasso回归:
每条曲线对应一个变量。它显示了当λ变化时,它的系数相对于整个系数向量的ℓ1范数的路径。上面的轴表示在当前λ非零系数的数量,这是lasso的有效自由度(df)。用户可能还希望对曲线进行注释:这可以通过在plot命令中设置label = TRUE来实现。
岭回归:
能够明显观察到岭回归下变量始终大于0,即解释变量未有被筛选掉;而相比之下,弹性网与lasso回归在lambda改变时,部分变量消失了,不再进行模型解释。
我们可以通过如下代码得到序列范围内一个或多个λ处的模型系数:
获取超参数=0.1时的参数估计结果
coef(fit,s=0.1)
1.9 Glmnet模型评价方法
函数glmnet返回一系列模型供用户选择。在许多情况下,用户可能更喜欢软件来选择其中之一。交叉验证可能是完成该任务最简单、使用最广泛的方法。简历。Glmnet是这里进行交叉验证的主要函数,以及各种支持方法,如绘图和预测。
十折交叉验证进行模型评价:
cvfit <- cv.glmnet(data_x, data_y,nfolds = 10)
cv.glmnet返回cv.glmnet对象,一个包含交叉验证匹配的所有成分的列表。与glmnet一样,不鼓励直接使用该对象,而是利用其软件包设计的函数。
绘图展示超参数的影响:
plot(cvfit)
这将绘制交叉验证曲线(红色虚线)以及沿λ序列(误差条)的上下标准偏差曲线。沿着λ序列的两个特殊值用垂直的虚线表示。
1.10 Glmnet选择最佳模型
打印最佳的超参数 帮助用户选择:
lambda.min下的模型交叉验证误差最小。lambda.1se给出了最正则化的模型,使得交叉验证误差在最小值的一个标准误差内。
print(cvfit$lambda.min)
print(cvfit$lambda.1se)
> print(cvfit$lambda.min)
[1] 0.02866132
> print(cvfit$lambda.1se)
[1] 0.07266689
1.11 Glmnet预测
设置种子 随机生成新数据
set.seed(29)
nx <- matrix(rnorm(500 * 30), 500, 30)
通过已经训练好的模型 进行预测
predict(fit, newx = nx, s = c(0.1, 0.05))
> predict(fit, newx = nx, s = c(0.1, 0.05))
s1 s2
[1,] 2.7309311 2.7732605
[2,] 2.2859731 2.2954917
[3,] 2.2992034 2.3208074
[4,] 1.6894255 1.6735020
[5,] 2.5623190 2.5941302
[6,] 1.5733710 1.5388561