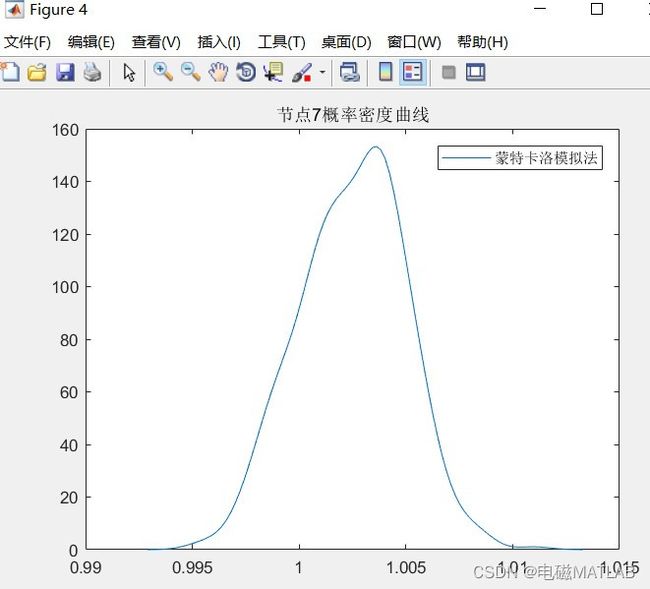
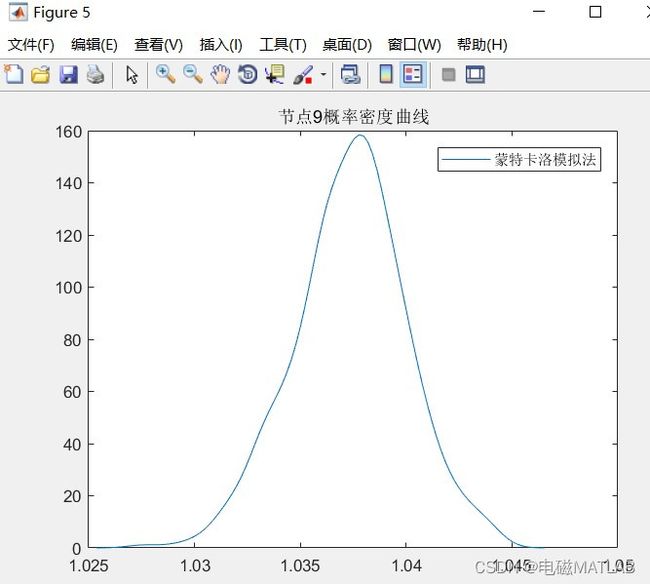
基于拟蒙特卡洛模拟法的随机潮流计算matlab程序

电力系统随机潮流计算中常采用模拟法，该方法原理简单、使用方便，能够精确地模拟实际物理过程，但是简单的蒙特卡洛模拟法收敛速度很慢，要得到精确的结果需要以大量的计算时间为代价。本章在此基础上提出了基于拟蒙特卡洛模拟的随机潮流计算方法，并且对拟蒙特卡洛法中的拟随机数序列进行了改进，大大提高了随机潮流的计算效率。
参考文献：考虑光伏功率相关性的随机潮流计算方法

1 蒙特卡洛法
蒙特卡洛模拟法（Monte Carlo Method），又称为随机模拟法，主要是应用了计算机中生成的“随机数”。

基于概率论原理，通过大量模拟实验可以近似求得某一事件发生的概率。当实验的样本数目接近于无穷大时，模拟事件发生的频率就会无限接近于事件发生的真实概率。

模拟法的具体思路如下：基于实际工程问题的求解需要，建立与之相对应的随机模拟过程和随机概率模型，使得它们的参数，包括概率分布或者数学期望，能够等于问题的实际解；最后采用模拟抽样实验求解参数中的统计特征量，所求解的值一般采用其算术平均值近似表示。

如果X为离散型随机变量，则函数g(x)的期望值计算表达式如下式所示：

如果X为连续型随机变量，则函数g(x)的期望值计算表达式如下式所示：

其中f(x)为随机变量X的概率密度函数。

（x1,x2,x3,…,xn）表示取自总体X的n个随机样本，基于样本值，可以求出g(x)的均值，采用蒙特卡洛估计法可以估计得到E(g(X))：

基于模拟法得到的最终解仅仅是一个估计值，而不是该问题的实际解，因
此必定存在误差。在方差的基础上，分析蒙特卡洛模拟法的误差。

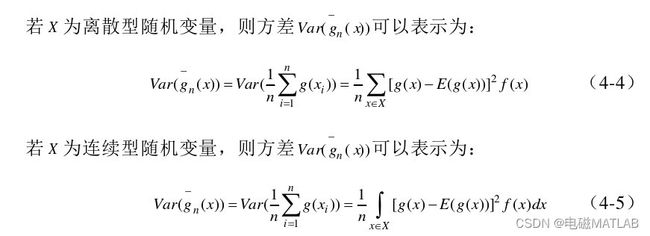
在柯尔莫哥洛夫大数定理的基础上，随机变量g (x i ),i=1,2,3,…,n相互独立，并且服从同一概率分布，如果数学期望值存在，那么，

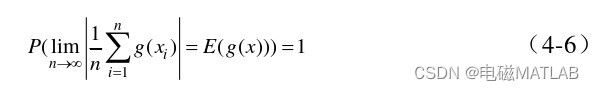
由上式可知，当n无穷大时，蒙特卡洛模拟中的随机变量估计值gn(x)以概率1收敛于E(g(x))。

在中心极限定理的基础上，随机变量g (x i), i=1,2,3,…,n相互独立，并且服从同一概率分布，如果数学期望值存在，并且方差Var不等于0 ，那么n趋于无穷大时

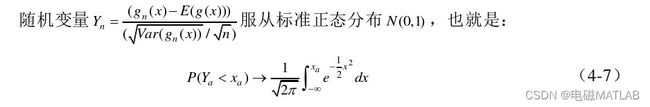
模拟法中，随机变量g (x i), i=1,2,3,…,n均满足上述条件，则任意xa>0，都存在：

上式中的a与ax可以通过查找积分表可知。当置信度a给定以后，蒙特卡洛模拟法的误差值由方差与样本容量来决定。
此处采用方差系数来表示模拟误差：

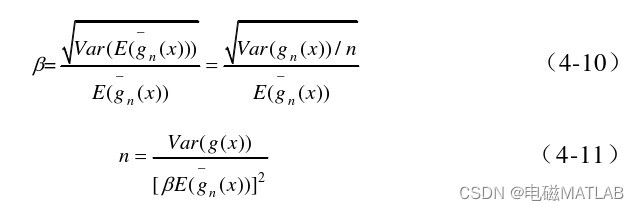
由式（4-11）可知，蒙特卡洛模拟法的计算量不受电力系统规模大小影响，因此该方法在一些复杂的电力系统中可以得到应用，包括处理电力系统中有多个间歇性新能源接入的问题，解决系统中多个节点之间相关性问题等等。蒙特卡洛模拟法的计算量与方差系数的平方呈反比，与方差呈正比关系。因此在一定的精度要求下，减小方差是加快计算效率的一种手段，目前文献中最为常用的减少方差技术主要包括重要度采样法和拉丁超立方抽样法。但是以上几类方法不能保证随机数序列的低偏差性，误差的收敛速度阶仍旧保持，无法从本质上提高计算效率。文献[57]提出了基于低偏差序列的拟蒙特卡洛法，并且说明了拟蒙特卡洛法的收敛性能更优、收敛速度更快，从本质上可以克服收敛性的瓶颈。

2 算例

3 算例结果
各节点概率密度（列举五个）：