《机器学习实战》8.2 线性回归基础篇之预测鲍鱼年龄

《机器学习实战》8.2 线性回归基础篇之预测鲍鱼年龄

搜索微信公众号:‘AI-ming3526’或者’计算机视觉这件小事’ 获取更多人工智能、机器学习干货
csdn：https://blog.csdn.net/baidu_31657889/
github：https://github.com/aimi-cn/AILearners

本文出现的所有代码，均可在github上下载，不妨来个Star把谢谢~：Github代码地址

一、引言

前面讲述了回归的基础概念，现在我们要把回归应用于真实数据。

二、线性回归基础篇之预测鲍鱼年龄

在abalone.txt文件中记录了鲍鱼（一种水生物→__→）的年龄，这个数据来自UCI数据集合的数据。鲍鱼年龄可以从鲍鱼壳的层数推算得到。

数据集下载地址：数据集下载

数据集的数据如下：

我们可以看出来数据集是多维的，所以我们是很难画出来他们的分布状态的，每个维度代表什么意思也没给出，不过没事，我们只知道最后一列代表的是y值就可以啦。最后一列代表的是鲍鱼的真实年龄，前面几列的数据是一些鲍鱼的特征，例如鲍鱼壳的层数等。我们不做数据清理，直接用上所有特征，测试下我们的局部加权回归。

新建一个abalone.py文件，添加rssError函数，用于评价最后回归结果。编写代码如下：

#!/usr/bin/env python
# -*- encoding: utf-8 -*-
'''
@File    :   abalone.py
@Time    :   2019/07/08 14:50:05
@Author  :   xiao ming 
@Version :   1.0
@Contact :   [email protected]
@Desc    :   线性回归基础篇之预测鲍鱼年龄
@github  :   https://github.com/aimi-cn/AILearners
'''

# here put the import lib
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np

'''
@description: 加载数据
@param : fileName - 文件名
@return:  xArr - x数据集
          yArr - y数据集
'''
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t')) - 1
    xArr = []; yArr = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr

'''
@description: 使用局部加权线性回归计算回归系数w
@param : testPoint - 测试样本点
        xArr - x数据集
        yArr - y数据集
        k - 高斯核的k,自定义参数
@return: testPoint * ws - 测试点*回归系数->预测结果
'''
def lwlr(testPoint, xArr, yArr, k = 1.0):
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    #创建权重对角矩阵
    weights = np.mat(np.eye((m)))
    #遍历数据集计算每个样本的权重
    for j in range(m):
        diffMat = testPoint - xMat[j, :]                                 
        weights[j, j] = np.exp(diffMat * diffMat.T/(-2.0 * k**2))
    xTx = xMat.T * (weights * xMat)                                        
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆").decode('utf-8').encode('gb2312')
        return
    #计算回归系数
    ws = xTx.I * (xMat.T * (weights * yMat))                            
    return testPoint * ws

'''
@description: 局部加权线性回归测试
@param : testArr - 测试数据集,测试集
        xArr - x数据集,训练集
        yArr - y数据集,训练集
        k - 高斯核的k,自定义参数
@return: ws - 回归系数
'''
def lwlrTest(testArr, xArr, yArr, k=1.0):
    #计算测试数据集大小
    m = np.shape(testArr)[0]                                           
    yHat = np.zeros(m)    
    #对每个样本点进行预测
    for i in range(m):                                                    
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat
'''
@description: 计算回归系数w
@param : xArr - x数据集
        yArr - y数据集
@return: ws - 回归系数
'''
def standRegres(xArr,yArr):
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    #根据文中推导的公示计算简答回归系数
    xTx = xMat.T * xMat                           
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws
'''
@description: 误差大小评测函数
@param : yArr - 真实数据
        yHatArr - 预测数据
@return: 误差大小
'''
def rssError(yArr, yHatArr):
    return ((yArr - yHatArr) **2).sum()

if __name__ == "__main__":
    abX, abY = loadDataSet('C:/Users/Administrator/Desktop/blog/github/AILearners/data/ml/jqxxsz/8.Regression/abalone.txt')
    print('训练集与测试集相同:局部加权线性回归,核k的大小对预测的影响:')
    yHat01 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
    yHat1 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1)
    yHat10 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
    print('k=0.1时,误差大小为:',rssError(abY[0:99], yHat01.T))
    print('k=1  时,误差大小为:',rssError(abY[0:99], yHat1.T))
    print('k=10 时,误差大小为:',rssError(abY[0:99], yHat10.T))
    print('')

    print('训练集与测试集不同:局部加权线性回归,核k的大小是越小越好吗？更换数据集,测试结果如下:')
    yHat01 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
    yHat1 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1)
    yHat10 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
    print('k=0.1时,误差大小为:',rssError(abY[100:199], yHat01.T))
    print('k=1  时,误差大小为:',rssError(abY[100:199], yHat1.T))
    print('k=10 时,误差大小为:',rssError(abY[100:199], yHat10.T))
    print('')

    print(u"训练集与测试集不同:简单的线性归回与k=1时的局部加权线性回归对比:")
    print(u"k=1时,误差大小为:", rssError(abY[100:199], yHat1.T))
    ws = standRegres(abX[0:99], abY[0:99])
    yHat = np.mat(abX[100:199]) * ws
    print(u'简单的线性回归误差大小:', rssError(abY[100:199], yHat.T.A))

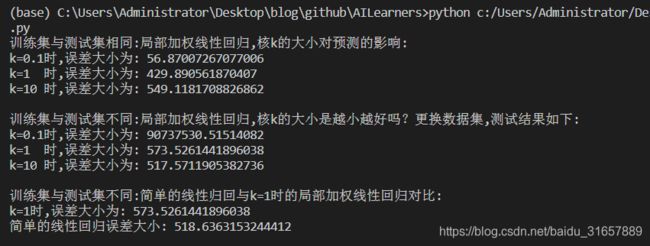
运行结果如下：

可以看到，当k=0.1时，训练集误差小，但是应用于新的数据集之后，误差反而变大了。这就是经常说道的过拟合现象。我们训练的模型，我们要保证测试集准确率高，这样训练出的模型才可以应用于新的数据，也就是要加强模型的普适性。可以看到，当k=1时，局部加权线性回归和简单的线性回归得到的效果差不多。这也表明一点，必须在未知数据上比较效果才能选取到最佳模型。那么最佳的核大小是10吗？或许是，但如果想得到更好的效果，应该用10个不同的样本集做10次测试来比较结果。

本示例展示了如何使用局部加权线性回归来构建模型，可以得到比普通线性回归更好的效果。局部加权线性回归的问题在于，每次必须在整个数据集上运行。也就是说为了做出预测，必须保存所有的训练数据。

下篇文章将继续讲解回归，会介绍另一种提高预测精度的方法。

AIMI-CN AI学习交流群【1015286623】 获取更多AI资料
扫码加群：

分享技术，乐享生活：我们的公众号计算机视觉这件小事每周推送“AI”系列资讯类文章，欢迎您的关注！