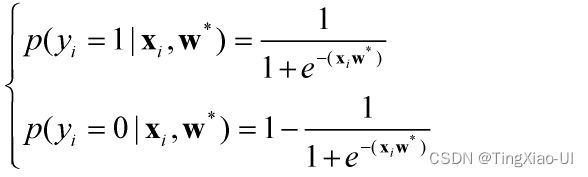逻辑回归算法原理

        回归与分类的不同在于其目标变量是否是连续的。分类是预测出一个标签，找到一条线或超平面去区分数据，输出是离散的、有限的。回归是预测出一个量，找到一条线去尽可能的拟合逼近这些数据，输出是连续的、无限的。

        逻辑回归本质上是线性回归套用激活函数sigmoid来输出概率值用于分类，如sigmoid(线性回归)=逻辑回归，如下所示

 适用于逻辑回归的场景：

        已知训练数据线性分布或者采用线性分布模型，但存在一些"异常/极端"值会使整个训练数据远远偏离了原有的正常范围-->会导致评估结果误差大，不准确。如下图黄色样本点为异常点

        这些"极端"值对整体数据的分布影响非常大。在数学中我们通常会采取一些平滑函数去减小这些"极端"值对整体分布的影响，从而使数据整体分布更加集中，比如最常见的Sigmoid函数。如下图所示

        可以看出通过sigmoid函数的映射，我们可以把极端值产生的影响变得非常微小，从而使其造成误判的结果尽可能降低。sigmoid函数表达式如下所示

借助sigmoid函数我们可以把分类(判别属于哪个类别)结果转换为一个计算样本属于某个类别的概率，如下图所示

构建目标函数      

        但是如何使用逻辑回归做分类呢？首先，逻辑回归的本质还是线性回归，我们需要先构建一个线性回归方程用来拟合数据点，如下图所示的红线，观察图中蓝色线段的长度总和就是预测值与真实值之间的整体误差和，如果某一条直线对应的整体误差值最小，也就表示这条直线最能反映数据点的分布趋势。那么误差如何表示？

        在线性回归中，使用残差的平方(RSS)和来表示所有样本点的误差，如下所示：

         根据代价函数计算出线性回归方程表达式

          然后借助激活函数sigmoid将离散值(预测值)映射为概率输出，如下所示

 对于二分类问题，y∈[0,1]，对于样本:1*(n+1)，分类器能够预测其类别为y的概率为

 对于样本X:m*(n+1)，分类器能够预测样本X的类别为Y的概率输出为

注意：这里的p(Y|X,w)表示观测值和参数的联合分布概率，不是条件概率。       

        如何求解参数w？在求解未知系数向量w的过程中，我们肯定需要有一个依据，那这个依据是什么呢？就是所谓的目标函数，所以每一个模型都对应一个目标函数，也就是我们想最优化的一个函数。基于这样的数据信息，我么可以定义下面的一个最大似然(MLE)，我们假定的逻辑回归模型，生成了这些我们所看到的样本数据，最大化样本发生的概率，即计算最具有可能（最大概率）导致这些 样本结果出现的模型参数值w， 因为你手头上的样本已经实现了，其发生概率最大才符合逻辑。然后在逻辑回归模型中，我们通过这种条件概率的方式把它考虑进来，对于每一个样本在最大似然里面，我们需要考虑所有的样本发生概率，通过乘积的方式把他们考虑进来，我们要找出使目标函数最大化的系数向量w。如下所示

注意：概率连乘可能会导致下溢，可以使用对数函数使连乘转换为累加。此外，一般情况下我们优化一个目标函数的时候，更倾向于一个最小化的目标函数，以最小化的方式求出系数向量w，所以如果我们的目标函数是最大化的话，我们通常在目标函数的前面加一个负号，然后使得我们可以找出它的最小值对应的最优解。

注意： 对数函数是一个严格递增的函数，取对数后不会改变数据的相对关系，即对数化后，我们仍然可以获得具有相同临界点的最优化目标函数。

       已知激活函数求导公式如下：

        使用梯度下降方法，不断迭代循环更新系数向量 w直到目标函数收敛，即达到极值点时我们获取到目标函数取得极值对应的参数 w。更多关于梯度下降方法见文章 常见迭代优化算法解析及python实现

假设对数函数的底数为e。参数 w的偏导数如下：

上述求导过程可矢量化表示为如下

通过梯度下降的方法得到最优参数，最终得到逻辑回归方程

  注意：

这里所谓的概率并不能代表样本真实的概率，只是一种映射结果而已。 回归到本质，sigmoid只是一种激活函数而已，激活函数的作用就是将一种值域映射成另一种值域，逻辑回归使用sigmoid函数将值域[-∞，+∞]映射到[0，1]，映射结果是一种概率形式而已，并不能代表样本真实的类别条件概率，其作用更多只是用于比较大小来实现分类。也因此逻辑回归只是一种判别模型，即不假设数据的分布，只考虑特征与标签的映射关系。

也可以用其他迭代优化方法求解参数w，见文章常见迭代优化算法解析及python实现

注意：

        在逻辑回归中我们通过极大似然定义了目标函数模型即交叉熵函数，而在线性回归中我们定了平方误差(MSE)的代价函数作为目标函数模型，那么在逻辑回归中能否使用平方误差(MSE)的代价函数作为目标函数模型呢？在线性回归中，我们通过梯度下降的方法不断迭代更新递进系数直到代价函数收敛，得到局部最优解，并且由于线性分布数据的代价函数一般都是凸函数，所以得到的局部最优解就是全局最优解，那么在逻辑回归中如果使用平方误差(MSE)的代价函数作为目标函数模型，那么目标函数是否是凸函数呢?  假设在逻辑回归中如果使用 平方误差(MSE)的代价函数作为目标函数模型，目标函数如下所示

         而此时的目标函数其二阶导数不恒大于0，为非凸函数(证明过程待补充)，所以在逻辑回归中如果使用平方误差(MSE)的代价函数作为目标函数为非凸函数，无法保证求得全局最优解，不能使用 平方误差(MSE)的代价函数，而要通过极大似然方法定义交叉熵函数为目标函数。

逻辑回归正则化

 上述过程得到的目标函数为

        正则项是对现在目标函数的惩罚项，正则项用来惩罚权重大的参数。正则化项可以起到简化模型的作用，通过约束参数的范数来防止过拟合。

加入L2正则化项的逻辑回归目标函数为

加入L2正则化项的逻辑回归目标函数等价于逻辑回归目标函数加约束条件，就是拉格朗日乘子法和KKT条件，约束条件为不等式约束的形式，如下所示

 等价目标函数如下所示

 式中t为某个阈值，只不过这个t有在目标函数里面体现，但是也没什么影响，因为目标函数一求偏导数这些常数就都没有了。

更多关于拉格朗日乘子法内容见文章常见迭代优化算法解析及python实现

 参数w的偏导数如下：

 上述求导过程可矢量化表示之前过程类似，只需要添加即可

和之前步骤类似，使用梯度下降或其他迭代优化方法，求解参数 ，最终得到逻辑回归方程

与不加正则化项的逻辑回归目标函数相比，加了正则化项后，的每一个元素均被均匀衰减，从而保证了不会出现某列特征的权重参数过大或过小，从而实现防止过拟合效果。