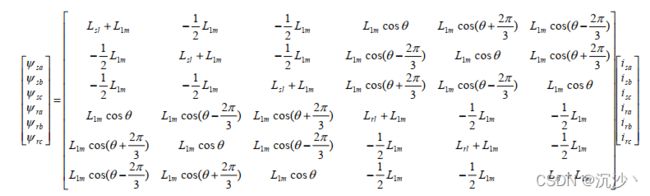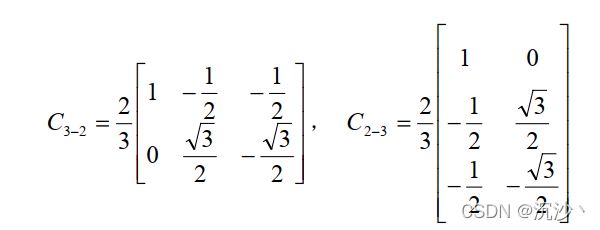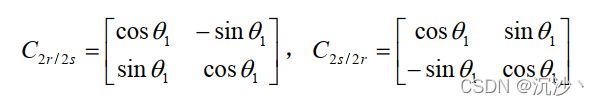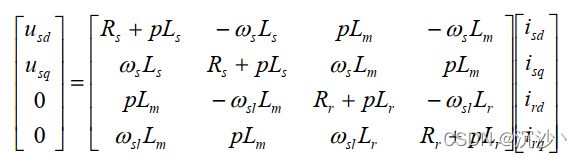交流异步电机矢量控制(一)——电机模型及其坐标变换
目录
1 异步电机在三相静止坐标系下的数学模型
1.1 电压方程
1.2 磁链方程
1.3 转矩方程
1.4 运动方程
小结:
2 异步电机在两相静止坐标系中的数学模型
1.2.1 恒功率原则下三相/两相静止坐标变换
1.2.2 恒相电流幅值三相/两相静止坐标变换
1.2.3 两相静止坐标系电机模型
3 异步电机在两相旋转坐标系中的数学模型
总结:
前言:随着国内工业自动化技术的发展,电机作为产线的动力核心,其控制技术的要求也越来越高,电机控制技术在制造业领域的重要程度也逐年增强。其中异步电机作为控制技术最成熟的电机种类之一,其应用范围最为广泛,因此有必要对其控制技术进行深入研究。博客前期更新内容永磁同步电机的内容较多,异步电机的内容非常少,其实也是因为我在学习的过程中,总是在畏惧异步电机这个四阶模型的电机,他相对于同步电机确实要难一些。本文记录异步电机的学习过程,由于这方面也是初学可能理解不够,每个部分内容出处都会标注出来,大家可以参照原文原著。博客大家都是以直接了当的获得想要结果为主,因此后续文章均以一个问题为切入点进行记录。
本篇博客解决的目标问题:异步电机不同坐标系的数学模型
1 异步电机在三相静止坐标系下的数学模型
在研究异步电机数学模型之前,为了排除机械制造安装、环境因素等的影响,需要对电机进行一定的理想化假设:
- 三相定子绕组和三相转子绕组在空间中对称分布,各相电流所产生的磁动势在气隙空间按正弦分布
- 涡流、磁饱和效应和铁芯损耗忽略不计
- 不考虑温度和频率变化对电机参数造成的影响
需要明确的是,后续研究的内容均以鼠笼型异步电机为对象,鼠笼型电机转子是短路的,即转子端电压为零。根据上述理想化假设可以构建异步电机在三相静止坐标系下的数学模型。
1.1 电压方程
电机六个绕组的电压矩阵方程可表示为:
电机的电压方程是一个六阶的数组,相对dq轴的电压模型来说模型阶层是较高的,这也是后续需要进行坐标变换的原因。式中 Rs 和 Rr 分别为定子电阻和折算到定子侧的转子电阻;is(abc)为定子三相电流;ir(abc)为折算到定子侧的转子三相电流;p为微分算子;phis(abc)为三相定子磁链;phir(abc)为折算到定子侧的三相转子磁链。
1.2 磁链方程
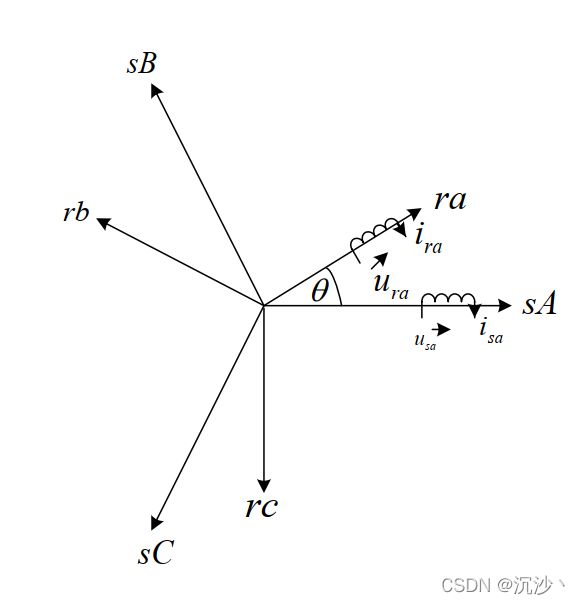
根据电机各绕组的空间位置,假设电机各相绕组如下图所示,
在电压、电流、磁链三者的正方向都符合右手螺旋定则时,电机六个绕组的磁链矩阵方程可以被表示为,式中,Lsl 、Lrl 为定子漏感和折算到转子侧的转子漏感,L1m 为主磁通对应的定子电感,![]() 为定子A轴和转子A轴之间的空间夹角。
为定子A轴和转子A轴之间的空间夹角。
1.3 转矩方程
根据载流导体在磁场中受力的基本公式可以得到电机的电磁转矩方程,如下所示。式中,np 为电机极对数,从方程结构可以看出,电机转矩是定子电流 is(abc)、转子电流 ir(abc)以及 定转子空间角度 ![]() 的函数,这是一个多变量的、强耦合的方程,非常不利于直接控制。
的函数,这是一个多变量的、强耦合的方程,非常不利于直接控制。
1.4 运动方程
一般情况下,如果将摩擦阻力合并到负载转矩 TL 中,电机的运动方程如下所示。式中,Te 为电机输出的电磁转矩,![]() 为转子旋转电气角速度。这里也有用机械角速度
为转子旋转电气角速度。这里也有用机械角速度 ![]() 来表示的,其实本质是一致的,因为电机转子旋转电气角速度和机械角速度之间存在固定的比例关系(比例为极对数),即
来表示的,其实本质是一致的,因为电机转子旋转电气角速度和机械角速度之间存在固定的比例关系(比例为极对数),即 ![]() = np *
= np * ![]() 。
。
小结:
根据对上述四个方程的分析可知,首先构成异步电机在ABC三相静止坐标系的数学模型是较为困难的,其次电机关键输出电机转矩是一个多变量、强耦合数学方程,单一变量的控制无法决定电机转矩的精准输出,因此在控制过程中相对较为困难。而对于我们做自动化控制而言,理想的控制状态就是唯一变量控制唯一输出变量,有需求就会有钻研,也就有了后续电机领域关键的突破——坐标变换。
2 异步电机在两相静止坐标系中的数学模型
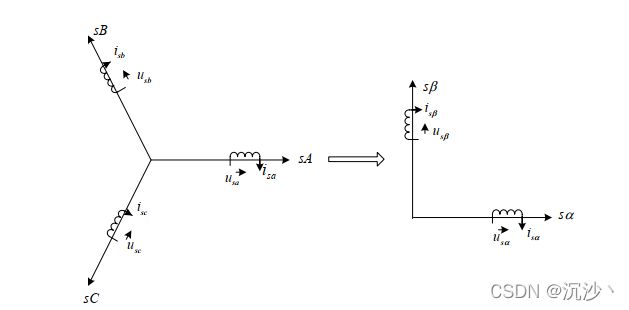
为了降低系统的阶数,降低控制难度,需要对异步电机的数学模型进行简化,将电机模型从三相静止坐标系变换到两相静止坐标系能够降低系统的阶数。三相/两相静止坐标变换又叫做Clark变换,是以空间位置固定的两相静止绕组代替电机实际三相绕组。下图为三相/两相静止坐标变换示意图:
令静止两相坐标系的 α轴 与定子 A轴 线重合,β轴 超前 α轴90°。在此基础上,假设电流、电压、磁链遵循同一个线性变换的关系,则可以得到三相/两相静止坐标变换的一般关系式。(若这里对一般关系式详细的推导过程有需要探究的同学,可以翻看陈伯时电力拖动中书籍的198页)
式中 y 代表电机定转子侧的电流、电压、磁链等变量,![]() 与
与 ![]() 为坐标变换系数,
为坐标变换系数,![]() 与
与 ![]() 为坐标变换矩阵。顺便值得指出的是,以上坐标变换都是基于电机定子侧进行的,也可以基于转子侧进行,但是不经常使用。
为坐标变换矩阵。顺便值得指出的是,以上坐标变换都是基于电机定子侧进行的,也可以基于转子侧进行,但是不经常使用。
相信有过接触的同学应该了解,三相/两相静止坐标变换是有两种的(一种是恒功率变换,一种是恒幅值变换),为什么会有这种区别呢?这里需要回归一定的线性代数知识,由于三相/两相变换前后独立变量个数不变,因此三相/两相变换其实是用新变量对原变量进行线性变换的过程,这个过程若依据的物理原则不同,变换的矩阵也就不同。目前已有的文献中,有关电机矢量控制的文献中采用的静止坐标变换原则并不统一,不同变换原则得到变换矩阵、电机转矩方程等都不同,非常容易引起混淆,为此本篇文章对这个问题进行针对性的解决。
1.2.1 恒功率原则下三相/两相静止坐标变换
基于恒功率的坐标变换是指变换前的三相电机和变换后的三相电机具有相同的功率和磁动势,即在电和磁两个方面完全等效,是基于等效电机原则的坐标变换。若定义三相系统和两相系统每相绕组匝数分别为 N3 和 N2,因为变换前后总磁动势不变,则有以下磁动势关系式:
所以变换矩阵 ![]() = N3 / N2 ,变换矩阵为。这里值得注意的是:不管是哪种原则的坐标变换,到磁动势这里都是完全一样的,区别产生的过程就在于下面的约束条件不同,从而导致变换矩阵的系数不同。在等功率变换时约束条件为变换前后功率相等;在等相电流幅值变换中,变换时约束条件为变换前后相电流幅值相等;在等矢量幅值变换中,变换时约束条件变为变换前后空间矢量的幅值相等。
= N3 / N2 ,变换矩阵为。这里值得注意的是:不管是哪种原则的坐标变换,到磁动势这里都是完全一样的,区别产生的过程就在于下面的约束条件不同,从而导致变换矩阵的系数不同。在等功率变换时约束条件为变换前后功率相等;在等相电流幅值变换中,变换时约束条件为变换前后相电流幅值相等;在等矢量幅值变换中,变换时约束条件变为变换前后空间矢量的幅值相等。
对于等功率变换而言,通过功率表达式可得以下关系式:
如果将恒功率变换的磁动势关系式 和 变换矩阵 带入上式,并结合三相/两相静止坐标变换的一般关系式可得 ![]() =
= ![]() = sqrt(2/3) 。由此可以得到三相/两相静止变换矩阵:
= sqrt(2/3) 。由此可以得到三相/两相静止变换矩阵:
根据变换矩阵对电机变换前后的电流、电压、磁链、功率等进行关系推导可得到以下结论:
- 等效两相绕组每相匝数 是 三相绕组每相匝数的 sqrt(3/2) 倍,即两相和三相的匝数比为 sqrt(3/2)
- 两相绕组中的定子相电流、转子相电流 和 相电压 均为三相绕组中的定子相电流、转子相电流和相电压 sqrt(3/2) 倍
- 两相绕组每相的功率是三相绕组每相的功率的 1.5 倍,由于变换后电机相数变为变换前的 2/3倍,所以总功率不变
- 两相静止坐标系中转矩方程为:
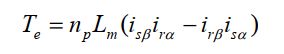
1.2.2 恒相电流幅值三相/两相静止坐标变换
对于恒矢量变换原则的线性变换,要求变换前后相电流幅值相等, 因此有
如果将磁动势方程 和 幅值表达式联立 ,即可得到 恒相电流幅值变换(等幅值变换)矩阵:
根据变换矩阵对电机变换前后的电流、电压、磁链、功率等进行关系推导可得到以下结论:
- 等效两相绕组每相匝数 是 三相绕组每相匝数的 sqrt(3/2) 倍。
- 两相绕组中的定子相电流、转子相电流 和 相电压 均等于三相绕组中的定子相电流、转子相电流和相电压 。
- 两相绕组每相的功率与三相绕组每相的功率相等,由于变换后电机相数变为变换前的 2/3倍,所以总功率变为变换前的 2/3 。
- 两相静止坐标系中转矩方程为

综合以上分析,不同的变换原则变换的匝数比都是相等的,变换前后磁动势都是相等的,恒相电流幅值变换前后,相电流电压未发生改变,但电机的总功率发生了改变,而恒功率变换前后,电机总功率未发生改变。从这个角度讲,恒相电流幅值变换可以认为是一种非等效变换,而恒功率变换可以被认为是等效变换。在实际应用中,应根据需求进行合理的选取。为了理解方便,选择恒功率的等效变换原则。下面基于恒功率变换建立两相静止坐标系的电机模型。
1.2.3 两相静止坐标系电机模型
(1)电压方程
(2)磁链方程
(3)转矩方程,转矩方程根据不同的物理变量有多种不同的表达式,实际应用过程中在以下方程中选择即可。
从以上方程可以看到,电机模型从六阶被降低为了四阶,此时的分析和控制相对于三相静止坐标系都更为简单快捷。但是从这些方程的表达式中,各个物理量均为交流量,是一个时变值。此时电机内部交流量在控制过程中是复杂的耦合的,若深入的探究分析可以发现控制变量还需要考虑电机转子与定子之间的夹角,在考虑物理量的幅值特性时,还需要考虑物理量的相位特性。要实现更优的控制性能,就需要将这些交流量转化为直流量去控制,仅需要控制其幅值特性即可。
3 异步电机在两相旋转坐标系中的数学模型
通过静止两相坐标变换,虽然异步电机的数学模型得到了简化,但是按照矢量控制原理,需要将这些交流量转化为直流量,这个过程就需要引入旋转坐标变换。三相静止到两相静止的函数推导较为复杂,但物理含义理解上并不困难,两相旋转变换数学推导并不困难,较为困难的地方是如何去理解旋转变换。
两相旋转坐标变换示意图如上所示,图中 sa为两相静止坐标系的横轴,sd 为旋转坐标系的横轴。变换前后系统的两相系统的匝数相等,按照变换前后磁动势等效的原则,可以得到以下关系式:
从而可以得到坐标变换矩阵为:
数学推导到这里就结束了,但是这个思想上呢为什么要这么变其实还没有搞清楚。引用一下大学老师讲的一个比喻,逆变器驱动电机的转动就像一个人在拉着一个圆环转动,由于磁场的极性特性,导致这个圆环有些特殊,他只有一个固定的地方可以用力。在两相静止坐标系中,我想要驱动圆环旋转,我就得一边控制自己双腿位置要和这个用力的地方匹配,一边还要控制自己的手出力推动转盘转起来,有时候控制不好了就转不动了,出的力也白出了。但是如果圆环的中间转盘,这个转盘能够时刻与圆环固定发力点匹配位置,我就可以站在这个转盘上,从此以后我不用再管我双脚的位置了,我就只用管我的手,我就只要狠狠的出力,出大力拉圆环转就行了,和出力点的匹配就交给转盘全权搞定了。这个时候控制圆环的转动就变得非常的简单了,就是出力,出大力,控制就解耦了。而两相旋转变换就等价于这个转盘的作用,我们看旋转坐标变换的矩阵里面有角度参数theta,其实就是因为转盘需要实时的和圆环的发力点匹配,这也是为什么矢量控制中必须要用到编码器、位置传感器等元件的原因,实际上就是为了得到这个theta。
(1)两相旋转坐标系中电压方程(基于转子磁链定向)
(2)两相旋转坐标系中磁链方程(基于转子磁链定向)
(3)两相旋转坐标系中转矩方程(基于转子磁链定向)
(4)转子磁链表达式
式中,taor为转子时间常数,从上述方程可以看出,经过基于转子磁链定向的旋转坐标变换后,定子电流的两个分量 isd 和 isq 两个分量实现了解耦。其中d轴分量 isd 唯一确定转子磁链的 phir 的稳态幅值,q轴分量 isq 只影响输出转矩的大小。“巧合”的是这两个电流分别与他励直流电机的励磁电流和电枢电流相对应,这样就大大简化了多变量、强耦合的交流异步电机调速系统的控制问题。
总结:
1、三相静止坐标系下异步电机的数学模型表现为多变量、非线性、强耦合的形式,直接对其求解十分困难。所以,需要引入恒功率、恒相幅值原则下的三相/两相静止坐标变换,得到异步电机简化的基于两相静止坐标系下的数学模型。
2、不管是哪种原则的坐标变换,合成磁动势都是完全一样的,区别产生的过程就在于约束条件不同,从而导致变换矩阵的系数不同。在等功率变换时约束条件为变换前后功率相等;在等相电流幅值变换中,变换时约束条件为变换前后相电流幅值相等;在等矢量幅值变换中,变换时约束条件变为变换前后空间矢量的幅值相等。
3、不同的变换原则变换的匝数比都是相等的,变换前后磁动势都是相等的,恒相电流幅值变换前后,相电流电压未发生改变,但电机的总功率发生了改变,而恒功率变换前后,电机总功率未发生改变。
4、两相静止坐标系中各个物理量均为交流量,是一个时变值。此时电机内部交流量在控制过程中是复杂的耦合的,若深入的探究分析可以发现控制变量还需要考虑电机转子与定子之间的夹角,在考虑物理量的幅值特性时,还需要考虑物理量的相位特性。要实现更优的控制性能,就需要将这些交流量转化为直流量去控制,仅需要控制其幅值特性即可。为了分析方便,进一步引入了dq两相旋转坐标系,将异步电机数学模型中的各物理量转换为在空间静止不动的直流量。当dq坐标系按转子磁场定向后,即可实现定子电流的解耦控制。
5、逆变器驱动电机的转动就像一个人在拉着一个圆环转动,由于磁场的极性特性,导致这个圆环有些特殊,他只有一个固定的地方可以用力。而两相旋转坐标变换的引入即是使得驱动器的功率能够精准作用到这个固定的地方,不仅提高了异步电机矢量控制的性能,还提高了系统的效率,但是这些高效的提升是基于theta精准的基础上,因此矢量控制的应用同时也对theta的精准获得提出了较高的要求。
综上,本篇博客解决的目标问题:异步电机不同坐标系的数学模型。解决完成,觉得还不错的话来个一键三~连。
在进行异步电机数学模型方面的学习之后,有需要了解异步电机的工作原理的同学可以看看这个视频,比较形象的讲解了异步电机磁、电与运动的关系:
【Motor】三相交流异步电机(感应电机 Induction Motor)是如何工作的_哔哩哔哩_bilibili
系列文章传送门:
1、交流异步电机矢量控制(一)——电机模型及其坐标变换
2、交流异步电机矢量控制(二)——矢量控制原理
3、交流异步电机矢量控制(三)——磁场定向
4、交流异步电机矢量控制(四)——simulink仿真搭建