常见的损失函数
1、损失函数的意义
机器学习中的监督学习本质上是给定一系列训练样本 ,尝试学习 的映射关系,使得给定一个 ,即便这个 不在训练样本中,也能够得到尽量接近真实 的输出 。而损失函数(Loss Function)则是这个过程中关键的一个组成部分,用来衡量模型的输出 与真实的 之间的差距,给模型的优化指明方向。
2、回归问题的损失函数
2.1 均方差损失
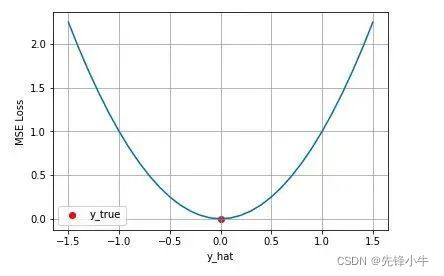
均方差 Mean Squared Error (MSE) 损失是机器学习、深度学习回归任务中最常用的一种损失函数,也称为 L2 Loss。
从直觉上理解均方差损失,这个损失函数的最小值为 0(当预测等于真实值时),最大值为无穷大。下图是对于真实值 ,不同的预测值 的均方差损失的变化图。横轴是不同的预测值,纵轴是均方差损失,可以看到随着预测与真实值绝对误差 的增加,均方差损失呈二次方地增加。
在模型输出与真实值的误差服从高斯分布的假设下,最小化均方差损失函数与极大似然估计本质上是一致的,因此在这个假设能被满足的场景中(比如回归),均方差损失是一个很好的损失函数选择;当这个假设没能被满足的场景中(比如分类),均方差损失不是一个好的选择 。
2.2 平方绝对误差损失
这个损失函数进行可视化如下图,MAE 损失的最小值为 0(当预测等于真实值时),最大值为无穷大。可以看到随着预测与真实值绝对误差 的增加,MAE 损失呈线性增长.
MSE 假设了误差服从高斯分布,MAE 假设了误差服从拉普拉斯分布。拉普拉斯分布本身对于 outlier 更加 robust。
2.3 Huber Loss (Smooth L1 Loss)
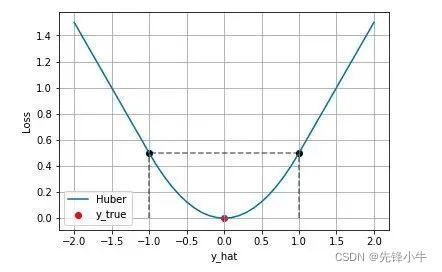
Huber Loss 则是一种将 MSE 与 MAE 结合起来,取两者优点的损失函数,也被称作 Smooth Mean Absolute Error Loss 。其原理很简单,就是在误差接近 0 时使用 MSE,误差较大时使用 MAE.
Huber Loss 结合了 MSE 和 MAE 损失,在误差接近 0 时使用 MSE,使损失函数可导并且梯度更加稳定;在误差较大时使用 MAE 可以降低 outlier 的影响,使训练对 outlier 更加健壮。缺点是需要额外地设置一个 超参数.
【不足】 Smooth L1 Loss在计算目标检测的 bbox loss时,都是独立的求出4个点的 loss,然后相加得到最终的 bbox loss。这种做法的默认4个点是相互独立的,与实际不符。举个例子,当(x, y)为右下角时,w h其实只能取0
2.4 分位数损失
分位数回归 Quantile Regression 是一类在实际应用中非常有用的回归算法,通常的回归算法是拟合目标值的期望或者中位数,而分位数回归可以通过给定不同的分位点,拟合目标值的不同分位数。例如我们可以分别拟合出多个分位点,得到一个置信区间,如下图所示(图片来自笔者的一个分位数回归代码 demo Quantile Regression Demo)
下图是取不同的分位点 0.2、0.5、0.6 得到的三个不同的分位损失函数的可视化,可以看到 0.2 和 0.6 在高估和低估两种情况下损失是不同的,而 0.5 实际上就是 MAE。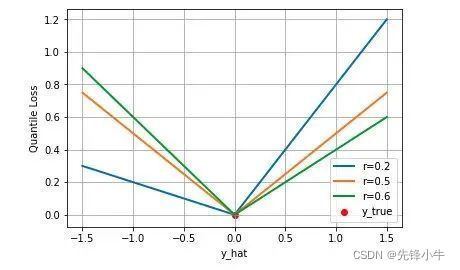
2.5 IoU Loss
【动机】 针对smooth L1没有考虑box四个坐标之间相关性的缺点,
【分析】 通过4个坐标点独立回归Building boxes的缺点:
检测评价的方式是使用IoU,而实际回归坐标框的时候是使用4个坐标点,如下图所示,是不等价的;L1或者L2 Loss相同的框,其IoU 不是唯一的;
通过4个点回归坐标框的方式是假设4个坐标点是相互独立的,没有考虑其相关性,实际4个坐标点具有一定的相关性;
实际使用中简化为:
【不足】
当预测框和目标框不相交,即 IoU(bbox1, bbox2)=0 时,不能反映两个框距离的远近,此时损失函数不可导,IoU Loss 无法优化两个框不相交的情况。
假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,其 IoU 值是相同时,IoU 值不能反映两个框是如何相交的。 EIoU Loss(2021)
EIoU Loss(2021)
论文地址:https://arxiv.org/pdf/2101.08158.pdf
【动机】 解决CIoU的定义中不足
【亮点】 引入了解决样本不平衡问题的Focal Loss思想
3 分类问题的损失函数
3.1 交叉熵损失函数
上文介绍的几种损失函数都是适用于回归问题损失函数,对于分类问题,最常用的损失函数是交叉熵损失函数 Cross Entropy Loss。
下图是对二分类的交叉熵损失函数的可视化,蓝线是目标值为 0 时输出不同输出的损失,黄线是目标值为 1 时的损失。可以看到约接近目标值损失越小,随着误差变差,损失呈指数增长。
多分类
在多分类的任务中,交叉熵损失函数的推导思路和二分类是一样的,变化的地方是真实值 现在是一个 One-hot 向量,同时模型输出的压缩由原来的 Sigmoid 函数换成 Softmax 函数。Softmax 函数将每个维度的输出范围都限定在 之间,同时所有维度的输出和为 1,用于表示一个概率分布。
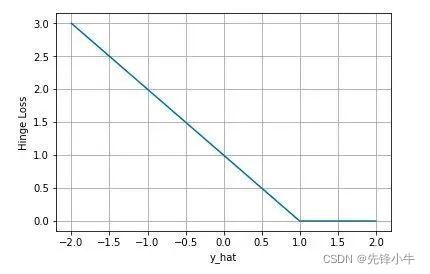
3.2 合页损失(Hinge Loss)
合页损失 Hinge Loss 是另外一种二分类损失函数,适用于 maximum-margin 的分类,支持向量机 Support Vector Machine (SVM) 模型的损失函数本质上就是 Hinge Loss + L2 正则化。