人工智能归结原理实验
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
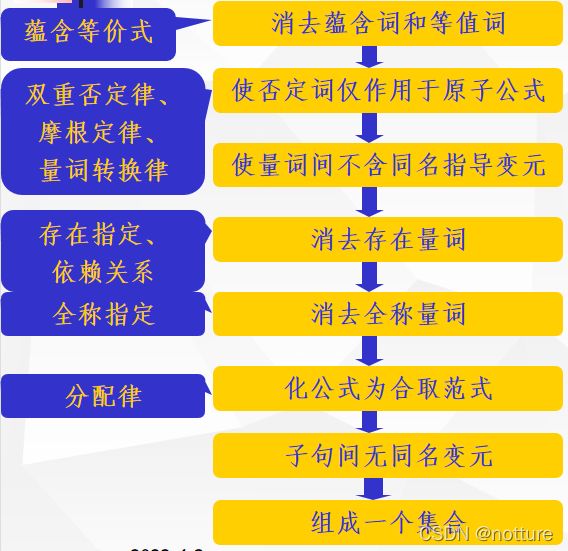
- 一、流程
- 二、步骤
-
- 0.声明
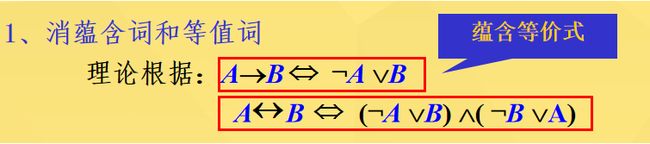
- 1.消去蕴含词和等值词
- 2.使否定词仅作用于原子公式
- 3.使量词间不含同名指导变元
- 4.化为前束范式
- 5.消去存在量词
- 6.消去全称量词
- 7.化公式为合(&)取范式
- 8.消去合取词,得到子句集
- 9.合一算法
- 10.归结原理
- 运行结果
-
-
- 1.
- 2.
- 3.
-
-
- 代码简陋,还请包涵
- 当时做的时候没想那么多,所以前面化简和后面归结存在一些问题。
-
-
前言
考察 命题逻辑归结推理
要求 熟悉C++迭代器使用,有一定离散数学基础
复杂式子无法实现
一、流程
二、步骤
0.声明
typedef string Formula;
typedef vector<string> SubsentenceSet;
typedef string::iterator FormulaIter;
typedef string::reverse_iterator FormulaRevIter;
// 公式符号定义
const char EQ = '#'; // 存在量词符号
const char UQ = '@'; // 全称量词符号
const char IMPLICATION = '>'; // 蕴含符号
const char NEGATION = '~'; // 否定符号
const char CONJUNCTION = '&'; // 合取符号
const char DISJUNCTION = '|'; // 析取符号
const char CONSTANT_ALPHA[] = {'a', 'b', 'c', 'd', 'e', 'i', 'j', 'k'};
const char FUNC_ALPHA[] = {'f', 'g', 'h', 'l', 'm', 'n', 'o'};
1.消去蕴含词和等值词
//消去蕴含连接词
Formula &RemoveImplication(Formula &f)
{
FormulaIter iter;
while ((iter = find(f.begin(), f.end(), IMPLICATION)) != f.end())//寻找蕴含符号
{
*iter = DISJUNCTION; // 将蕴含符号替换为析取符号
FormulaRevIter revIter(iter);
revIter = GetBeginOfFormula(revIter, f.rend()); // 查找蕴含前件
iter = revIter.base(); // 反向迭代器到正向迭代器
f.insert(iter, NEGATION); // 在前件前面插入否定
}
return f;
}
2.使否定词仅作用于原子公式
//将否定符号移到紧靠谓词的位置
Formula &MoveNegation(Formula &f)
{
FormulaIter iter = find(f.begin(), f.end(), NEGATION);
while (iter != f.end())
{
if (*(iter + 1) == '(')
{ // 否定不是直接修饰谓词公式,需要内移
// 否定符号修饰着带量词的谓词公式
if (*(iter + 2) == EQ || *(iter + 2) == UQ)
{
// 量词取反
*(iter + 2) == EQ ? *(iter + 2) = UQ : *(iter + 2) = EQ;
string leftDonePart(f.begin(), iter + 5);
// 移除否定符号
leftDonePart.erase(find(leftDonePart.begin(), leftDonePart.end(), NEGATION));
string rightPart(iter + 5, f.end());
// 否定内移
rightPart.insert(rightPart.begin(), NEGATION);
// 递归处理右部分
MoveNegation(rightPart);
string(leftDonePart + rightPart).swap(f);
return f;
}
else
{ // 修饰着多个公式,形如~(P(x)|Q(x))
iter = f.insert(iter + 2, NEGATION); // 内移否定符号
while (1)
{
iter = FindFormula(iter, f.end());
//assert(iter != f.end() && "No Predicate Formula!");
FormulaIter iter2 = FindPairChar(
iter, f.end(), '(', ')');
++iter2;
if (IsConnector(*iter2))
{
*iter2 == DISJUNCTION ? *iter2 = CONJUNCTION
: *iter2 = DISJUNCTION;
iter = f.insert(iter2 + 1, NEGATION);
}
else
break;
}
f.erase(find(f.begin(), f.end(),
NEGATION)); // 清除原否定符号
return MoveNegation(f);
}
}
else if (*(iter + 1) == NEGATION)
{ // 两个否定,直接相消
f.erase(iter, iter + 2);
return MoveNegation(f); // 重新处理
}
else
{
string leftDonePart(f.begin(), iter + 1);
string rightPart(iter + 1, f.end());
MoveNegation(rightPart);
string(leftDonePart + rightPart).swap(f);
return f;
//iter = find(iter + 1, f.end(), NEGATION);
}
}
return f;
}
3.使量词间不含同名指导变元
//适当改名使量词间不含同名指导变元,对变元标准化。
Formula &StandardizeValues(Formula &f)
{
set<char> checkedAlpha;
FormulaIter iter = FindQuantifier(f.begin(), f.end());
while (iter != f.end())
{
char varName = *++iter; // 获取变量名
if (checkedAlpha.find(varName) == checkedAlpha.end())
{
checkedAlpha.insert(varName);
}
else
{ // 变量名冲突了,需要改名
// 获取新名子
char newName = FindNewLowerAlpha(checkedAlpha);
checkedAlpha.insert(newName);
// 查找替换右边界
FormulaIter rightBorder = FindPairChar(
iter + 2, f.end(), '(', ')');
// 将冲突变量名替换为新的名子
*iter = newName;
replace(iter, rightBorder, varName, newName);
iter = rightBorder; // 移动到新的开始
}
iter = FindQuantifier(iter, f.end());
}
return f;
}
4.化为前束范式
//化为前束范式。
Formula &TransformToPNF(Formula &f)
{
FormulaIter iter = FindQuantifier(f.begin(), f.end());
if (iter == f.end())
return f;
else if (iter - 1 == f.begin())
{ // 量词已经在最前面
iter += 3;
string leftPart(f.begin(), iter);
string rightPart(iter, f.end());
TransformToPNF(rightPart); // 递归处理右部分
(leftPart + rightPart).swap(f);
}
else
{ // 量词在内部,需要提到前面
string quantf(iter - 1, iter + 3); // 保存量词
f.erase(iter - 1, iter + 3); // 移除量词
f.insert(f.begin(), quantf.begin(), quantf.end());
return TransformToPNF(f); // 继续处理
}
return f;
}
5.消去存在量词
//消去存在量词。
Formula &RemoveEQ(Formula &f)
{
set<char> checkedAlpha;
FormulaIter eqIter = find(f.begin(), f.end(), EQ);
if (eqIter == f.end())
return f;
FormulaRevIter left = leftleft(FormulaRevIter(eqIter), f.rend());
FormulaRevIter uqIter = findRev(left, f.rend(), UQ);
if (uqIter == f.rend())
{ // 该存在量词前没有任意量词
char varName = *(eqIter + 1);
char newName = GetNewConstantAlha(f);
auto rightBound = FindPairChar(eqIter + 3, f.end(), '(', ')');
//assert(rightBound != f.end());
replace(eqIter + 3, rightBound, varName, newName); // 常量化
f.erase(eqIter - 1, eqIter + 3); // 移除存在量词
}
else
{
// 记录公式中已经存在的字母
copy_if(f.begin(), f.end(), checkedAlpha);
const char oldName = *(eqIter + 1);
// 准备任意量词的函数来替换该存在量词
const char funcName = FindFuncAlpha(checkedAlpha);
string funcFormula;
funcFormula = funcFormula + funcName + '(' + *(uqIter - 1) + ')';
f.erase(eqIter - 1, eqIter + 3); // 移除存在量词
ReplaceAlphaWithString(f, oldName, funcFormula);
}
//RemoveOuterBracket(f, f.begin());
return RemoveEQ(f); // 递归处理
}
6.消去全称量词
//消去全称量词。
Formula &RemoveUQ(Formula &f)
{
FormulaIter uqIter = find(f.begin(), f.end(), UQ);
while (uqIter != f.end())
{
uqIter = f.erase(uqIter - 1, uqIter + 3); // 直接移除全称量词
uqIter = find(uqIter, f.end(), UQ); // 继续扫描
}
//RemoveOuterBracket(f, f.begin());
return f;
}
7.化公式为合(&)取范式
//化为合取范式。
Formula &TransformToConjunction(Formula &f)
{
FormulaIter dis = find(f.begin(), f.end(), DISJUNCTION);
FormulaRevIter left = leftfind((FormulaRevIter)dis, f.rend());
FormulaIter leftt = left.base() - 1;
FormulaIter right = rightfind(dis + 1, f.end());
FormulaRevIter leftcon = findRev((FormulaRevIter)dis, left, CONJUNCTION);
FormulaIter lefttcon = leftcon.base() - 1;
FormulaIter rightcon = find(dis, right, CONJUNCTION);
if (leftt != lefttcon && rightcon == right)
{
cout << string(dis + 1, right) << endl;
cout << string(leftt + 1, lefttcon) << endl;
cout << string(lefttcon + 1, dis) << endl;
string temp = "(" + string(dis + 1, right) + "|" + string(leftt + 1, lefttcon) + ")&(" + string(dis + 1, right) + "|" + string(lefttcon + 1, dis - 1) + ")";
// cout << temp << endl;
f.replace(leftt, right, temp);
}
else if (leftt == lefttcon && right != rightcon)
{
// cout << string(leftt + 1, dis) << endl;
// cout << string(dis + 1, rightcon) << endl;
// cout << string(rightcon + 1, right - 1) << endl;
string temp = "(" + string(leftt + 1, dis) + "|" + string(dis + 1, rightcon) + ")&(" + string(leftt + 1, dis) + "|" + string(rightcon + 1, right - 1) + ")";
// cout << temp << endl;
f.replace(leftt, right, temp);
}
else if (leftt != lefttcon && right != rightcon)
{
string str1 = string(leftt + 1, lefttcon);
string str2 = string(lefttcon + 1, dis);
string str3 = string(dis + 1, rightcon);
string str4 = string(rightcon + 1, right);
cout << str1 << endl;
cout << str2 << endl;
cout << str3 << endl;
cout << str4 << endl;
string temp;
if (str1 == str3)
{
temp = str1 + "&(" + str2 + "|" + str4 + ")";
}
else if (str1 == str4)
{
temp = str1 + "&(" + str2 + "|" + str3 + ")";
}
else if (str2 == str3)
{
temp = str2 + "&(" + str1 + "|" + str4 + ")";
}
else if (str2 == str4)
{
temp = str2 + "&(" + str1 + "|" + str3 + ")";
}
f.replace(leftt, right + 1, temp);
}
return f;
}
8.消去合取词,得到子句集
这里没有对子句做标准化,即不同的子句用不同的变元,和前面的标准化大同小异。
//消去合取词,以子句为元素组成一个集合S。
void ExtractSubsentence(SubsentenceSet &subset, Formula &f)
{
FormulaIter leftIter = f.begin();
FormulaIter middleIter = find(f.begin(), f.end(), CONJUNCTION);
while (middleIter != f.end())
{
if (*leftIter == '(' && *(middleIter - 1) == ')')
subset.push_back(string(leftIter + 1, middleIter - 1));
else
subset.push_back(string(leftIter, middleIter));
leftIter = middleIter + 1;
middleIter = find(middleIter + 1, f.end(), CONJUNCTION);
}
if (*leftIter == '(' && *(middleIter - 1) == ')')
subset.push_back(string(leftIter + 1, middleIter - 1));
else
subset.push_back(string(leftIter, middleIter));
}
9.合一算法
合一代码,直接调用syncretism函数。
bool syncretism(const string tf1, const string tf2, vector<transform> &mgu) //合一方法,判断是否可进行合一
{
string f1 = tf1, f2 = tf2;
while (!same(f1, f2)) //f1与f2中的符号不完全相同时才进入while循环
{
transform t = dif(f1, f2); //得到f1和f2的一个差异集,并把它赋给t
int flag = legal(t);
if (flag == 0)
return false;
else
{
mgu.push_back(t);
f1 = change(f1, mgu.back());
f2 = change(f2, mgu.back());
cout << "after change:" << endl;
cout << "f1:" << f1 << endl;
cout << "f2:" << f2 << endl;
if (same(f1, f2))
return true; //f1和f2相同时就停止循环
}
}
return false;
}
bool same(const string f1, const string f2) //判断两个谓词f1和f2是否相同
{
if (f1.length() == f2.length())
{
int i = 0;
while (i < f1.length() && f1.at(i) == f2.at(i))
i++;
if (i == f1.length())
return true;
else
{
return false;
}
}
else
return false;
}
transform dif(const string f1, const string f2) //求解f1和f2的差异集
{
int i = 0;
transform t;
while (f1.at(i) == f2.at(i)) //第i个相等时就转向比较i+1,直到遇到不相等时就跳出while循环
i++;
int j1 = i;
while (j1 < f1.length() - 1 && f1.at(j1) != ',') //从不相等的部分开始,直到遇到‘,’或到达结尾时跳出while循环
j1++;
if (j1 - i == 0)
return t;
t.t_f1 = f1.substr(i, j1 - i); //将f1中的不相同的项截取出来放入变量t.t_f1中
int j2 = i;
while (j2 < f2.length() - 1 && f2.at(j2) != ',')
j2++;
if (j2 - i == 0)
return t;
t.t_f2 = f2.substr(i, j2 - i); //将f2中的不相同的项截取出来放入变量t.t_f2中
while (t.t_f1[j1 - i - 1] == t.t_f2[j2 - i - 1]) //去除相同的部分
{
t.t_f1.erase(j1 - 1 - i);
t.t_f2.erase(j2 - i - 1);
j1--;
j2--;
}
return t;
}
int legal(transform &t) //判断置换t是否合法
{
if (t.t_f1.length() == 0 || t.t_f2.length() == 0)
return 0;
if (var(t.t_f2))
{
if (var(t.t_f1) && (varData(t.t_f1) == varData(t.t_f2))) //不能代换合一
return 0;
else
return 2;
}
if (!var(t.t_f1)) //若t_f1和t_f2都不是变量,也不能合一
return 0;
string temp;
temp = t.t_f1;
t.t_f1 = t.t_f2;
t.t_f2 = temp; //在t_f1是变量而t_f2不是变量的情况下,交换t_f1和t_f2
return 1;
}
string varData(string s) //该函数是剥去外层括号
{
if (s.length() == 1 || s.length() == 0)
return s;
if (s.length() > 1)
{
int i = 0;
while (i < s.length() && s.at(i) != '(')
i++;
int j = i;
while (j < s.length() && s.at(j) != ')')
j++;
string ss = s.substr(i + 1, j - i - 1);
return varData(ss);
}
}
bool var(const string s)
{
if (s.length() == 0)
return false;
if (s.length() == 1 && s[0] >= 'A' && s[0] <= 'Z')
return false;
if (s.length() > 1)
{
int i = 0;
while (i < s.length() && s.at(i) != '(') //略过不是'('的字符
i++;
int j = i;
while (j < s.length() && s.at(j) != ')') //略过')'前的字符
j++;
string ss = s.substr(i + 1, j - i - 1); //取出'('和')'之间的串
return var(ss); //递归调用var
}
else
{
return true;
}
}
string change(string f, transform q) //该函数查找t_f2在f中的位置并用t_f1替代f中相应的t_f2
{
int i = f.find(q.t_f2);
while (i < f.length())
{
i = f.find(q.t_f2);
if (i < f.length())
f = f.replace(i, q.t_f2.length(), q.t_f1);
}
return f;
}
10.归结原理
int finditer(string s, char a, char b)//*iter.find("~P")的时候莫名报错,于是手写查找。
{
for (int i = 0; i < s.length(); i++)
{
if (s[i] == a && s[i + 1] == b)
{
return i;
}
}
return 0;
}
bool resolution(SubsentenceSet &subset) //归结
{
for (vector<string>::reverse_iterator rbegin = subset.rbegin(); rbegin != subset.rend();) //从尾部,即目标公式开始归结
{
bool f = false;
bool rev = false; //是否取反
string s = *rbegin;
string ss;
FormulaIter left = s.begin();
FormulaIter middle = find(left, s.end(), DISJUNCTION);
string goal = string(left, middle); //归结元素
string _goal = pdrev(goal, rev); //归结元素的逆
vector<string>::reverse_iterator iter;
while (middle != s.end()) //寻找归结元素的逆,找到末尾结束
{
iter = findreviter(subset, _goal, rev);
if (iter == subset.rend()) //找不到继续循环
{
left = middle + 1;
middle = find(left, s.end(), DISJUNCTION);
goal = string(left, middle);
_goal = pdrev(goal, rev);
}
else
{
f = true; //找到标记
break;
}
}
if (!f) //判断是否找到,前面最后一个left和middle没有处理,这里继续处理。
{
iter = findreviter(subset, _goal, rev);
if (iter == subset.rend())
{
rbegin++;
continue;
}
}
ss = (*iter);
char cc = goal[0];
int len = goal.length();
if (rev)
{
cc = goal[1];
len -= 1;
}
dosyncretism(s.substr(s.find(cc), len), ss.substr(ss.find(cc), len), *iter); //合一
//擦除归结了的式子
(*rbegin).erase((*rbegin).find(goal), goal.length());
string c = "";
if (rev)
{
c += _goal[0];
(*iter).erase((*iter).find(_goal[0]), _goal.length());
}
else
{
c += _goal[0] + _goal[1];
(*iter).erase(finditer(*iter, _goal[0], _goal[1]), _goal.length());//这里~P找不到,于是手写寻找函数。
}
//(*iter).erase(*iter.find(c),_goal.length());找不到,
//合并剩余式子
string newstr = (*rbegin) + "|" + (*iter);
//擦除多余析取符
for (int i = 0; i < newstr.length(); i++)
{
if ((i == 0 || i == newstr.length() - 1) && newstr[i] == DISJUNCTION)
{
newstr.erase(i, 1);
i -= 1;
}
else if (newstr[i] == DISJUNCTION && newstr[i + 1] == DISJUNCTION)
{
newstr.erase(i + 1, 1);
}
}
cout << endl;
//删除旧的式子,添加新的式子。
subset.erase(subset.rbegin().base());
subset.erase(iter.base() - 1);
subset.push_back(newstr);
rbegin = subset.rbegin();
count(subset);
//归结出空,则结论为真,归结结束。
if (newstr == "")
{
return true;
}
}
return false;
}
运行结果
1.
Input:
(@x)(D(x)>(B(x)&F(x)))&(@x)(F(x)>N(x))&(@x)(G(x)>D(x))&~(@x)(G(x)>N(x))
Elimination of implied symbols://消去蕴含
(@x)(~D(x)|(B(x)&F(x)))&(@x)(~F(x)|N(x))&(@x)(~G(x)|D(x))&~(@x)(~G(x)|N(x))
Move the negation sign to the front of each predicate://处理非符
(@x)(~D(x)|(B(x)&F(x)))&(@x)(~F(x)|N(x))&(@x)(~G(x)|D(x))&(#x)(G(x)&~N(x))
Standardization of variables://变元标准化
(@x)(~D(x)|(B(x)&F(x)))&(@y)(~F(y)|N(y))&(@z)(~G(z)|D(z))&(#q)(G(q)&~N(q))
Eliminate existential quantifiers://消去存在
(@x)(~D(x)|(B(x)&F(x)))&(@y)(~F(y)|N(y))&(@z)(~G(z)|D(z))&(G(a)&~N(a))
Convert to a front bundle://化为前束
(@x)(@y)(@z)(~D(x)|(B(x)&F(x)))&(~F(y)|N(y))&(~G(z)|D(z))&(G(a)&~N(a))
Omit universal quantifiers://略去全称
(~D(x)|(B(x)&F(x)))&(~F(y)|N(y))&(~G(z)|D(z))&(G(a)&~N(a))
Standardization of Conjunction://化为合取式
(~D(x)|B(x))&(~D(x)|F(x))&(~F(y)|N(y))&(~G(z)|D(z))&G(a)&~N(a)
Eliminate the conjunction://子集
~D(x)|B(x)
~D(x)|F(x)
~F(y)|N(y)
~G(z)|D(z)
G(a)
~N(a)
after change://合一
f1:N(a)
f2:N(a)
mgu={ a/y }
~D(x)|B(x)
~D(x)|F(x)
~G(z)|D(z)
G(a)
~F(a)
after change:
f1:F(a)
f2:F(a)
mgu={ a/x }
~D(x)|B(x)
~G(z)|D(z)
G(a)
~D(a)
after change:
f1:D(a)
f2:D(a)
mgu={ a/z }
~D(x)|B(x)
G(a)
~G(a)
cannot be syncretized//相同变元无法合一
~D(x)|B(x)
//归结出空集,为真
Success
2.
Input:
~((#x)(P(x)&(@y)D(y)))
Elimination of implied symbols:
~((#x)(P(x)&(@y)D(y)))
Move the negation sign to the front of each predicate:
((@x)(~P(x)|(#y)~D(y)))
Standardization of variables:
((@x)(~P(x)|(#y)~D(y)))
Eliminate existential quantifiers:
((@x)(~P(x)|~D(f(x))))
Convert to a front bundle:
(@x)((~P(x)|~D(f(x))))
Omit universal quantifiers:
((~P(x)|~D(f(x))))
Standardization of Skolem:
((~P(x)|~D(f(x))))
Eliminate the conjunction:
(~P(x)|~D(f(x)))
Failure
3.
Input:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Elimination of implied symbols:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Move the negation sign to the front of each predicate:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Standardization of variables:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Eliminate existential quantifiers:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Convert to a front bundle:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Omit universal quantifiers:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Standardization of Skolem:
(~P(x)|Q(x))&(~P(y)|R(y))&S(a)&(~S(z)|~R(z))&P(a)
Eliminate the conjunction:
~P(x)|Q(x)
~P(y)|R(y)
S(a)
~S(z)|~R(z)
P(a)
after change:
f1:P(a)
f2:P(a)
mgu={ a/y }
~P(x)|Q(x)
S(a)
~S(z)|~R(z)
R(a)
after change:
f1:R(a)
f2:R(a)
mgu={ a/z }
~P(x)|Q(x)
S(a)
~S(a)
cannot be syncretized
~P(x)|Q(x)
Success
代码简陋,还请包涵
链接:https://pan.baidu.com/s/10yz6Yh83lEIpecEYdvhhuw
提取码:qwer