python 最优解 ma_AR(I)MA时间序列建模过程——步骤和python代码
1.异常值和缺失值的处理
这绝对是数据分析时让所有人都头疼的问题。异常和缺失值会破坏数据的分布,并且干扰分析的结果,怎么处理它们是一门大学问,而我根本还没入门。
(1)异常值
https://ocefpaf.github.io/python4oceanographers/blog/2015/03/16/outlier_detection/
提供了关于如何对时间序列数据进行异常值检测的方法,作者认为移动中位数的方法最好,代码如下:
from pandas import rolling_median
threshold = 3 #指的是判定一个点为异常的阈值df['pandas'] =
rolling_median(df['u'], window=3, center=True)
.fillna(method='bfill').fillna(method='ffill')
#df['u']是原始数据,df['pandas'] 是求移动中位数后的结果,
window指的是移动平均的窗口宽度difference = np.abs(df['u'] - df['pandas'])
outlier_idx = difference > threshold
rolling_median函数详细说明参见
(2)缺失值
缺失值在DataFrame中显示为nan,它会导致ARMA无法拟合,因此一定要进行处理。
a.用序列的均值代替,这样的好处是在计算方差时候不会受影响。但是连续几个nan即使这样替代也会在差分时候重新变成nan,从而影响拟合回归模型。
b.直接删除。我在很多案例上看到这样的做法,但是当一个序列中间的nan太多时,我无法确定这样的做法是否还合理。
2.平稳性检验
序列平稳性是进行时间序列分析的前提条件,主要是运用ADF检验。
from statsmodels.tsa.stattools import adfullerdef test_stationarity(timeseries):
dftest = adfuller(timeseries, autolag='AIC') return dftest[1]
#此函数返回的是p值
adfuller函数详细说明参见
3.不平稳的处理
(1)对数处理。对数处理可以减小数据的波动,因此无论第1步检验出序列是否平稳,都最好取一次对数。关于为什么统计、计量学家都喜欢对数的原因,知乎上也有讨论:
https://www.zhihu.com/question/22012482
(2)差分。一般来说,非纯随机的时间序列经一阶差分或者二阶差分之后就会变得平稳。那差分几阶合理呢?我的观点是:在保证ADF检验的p<0.01的情况下,阶数越小越好,否则会带来样本减少、还原序列麻烦、预测困难的问题。——这是我的直觉,还没有查阅资料求证。基于这样的想法,构造了选择差分阶数的函数:
(3)平滑法。利用移动平均的方法来处理数据,可能可以用来处理周期性因素,我还没实践过。
(4)分解法。将时间序列分解成长期趋势、季节趋势和随机成分,同样没实践过。
对于(3)(4),参见《》或者
4.随机性检验
只有时间序列不是一个白噪声(纯随机序列)的时候,该序列才可做分析。
from statsmodels.stats.diagnostic import acorr_ljungboxdef test_stochastic(ts):
p_value = acorr_ljungbox(ts, lags=1)[1] #lags可自定义
return p_value
acorr_ljungbox函数详细说明参见
http://www.statsmodels.org/devel/generated/statsmodels.stats.diagnostic.acorr_ljungbox.html?highlight=acorr_ljungbox#statsmodels.stats.diagnostic.acorr_ljungbox
5.确定ARMA的阶数
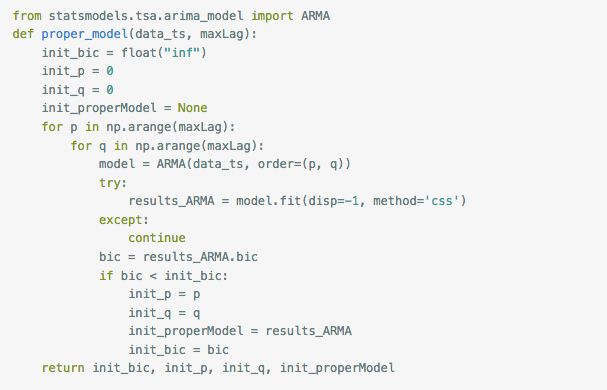
ARMA(p,q)是AR(p)和MA(q)模型的组合,关于p和q的选择,一种方法是观察自相关图ACF和偏相关图PACF, 另一种方法是通过借助AIC、BIC统计量自动确定。由于我有几千个时间序列需要分别预测,所以选取自动的方式,而BIC可以有效应对模型的过拟合,因而选定BIC作为判断标准。
这个函数的原理是,根据设定的maxLag,通过循环输入p和q值,选出拟合后BIC最小的p、q值。
然而在statsmodels包里还有更直接的函数:
import statsmodels.tsa.stattools as st
order = st.arma_order_select_ic(timeseries,max_ar=5,max_ma=5,ic=['aic', 'bic', 'hqic'])
order.bic_min_order
timeseries是待输入的时间序列,是pandas.Series类型,max_ar、max_ma是p、q值的最大备选值。
order.bic_min_order返回以BIC准则确定的阶数,是一个tuple类型
6.拟合ARAM
from statsmodels.tsa.arima_model import ARMA
model = ARMA(timeseries, order=order.bic_min_order)
result_arma = model.fit(disp=-1, method='css')
对于差分后的时间序列,运用于ARMA时该模型就被称为ARMIA,在代码层面改写为model = ARIMA(timeseries, order=(p,d,q)),但是实际上,用差分过的序列直接进行ARMA建模更方便,之后添加一步还原的操作即可。
7.预测的y值还原
从前可知,放入模型进行拟合的数据是经过对数或(和)差分处理的数据,因而拟合得到的预测y值要经过差分和对数还原才可与原观测值比较。
暂时写了对数处理过的还原:
def predict_recover(ts):
ts = np.exp(ts) return ts
8.判定拟合优度
在我学习计量经济学的时候,判断一个模型拟合效果是用一个调整R方的指标,但是似乎在机器学习领域,回归时常用RMSE(Root Mean Squared Error,均方根误差),可能是因为调整R方衡量的预测值与均值之间的差距,而RMSE衡量的是每个预测值与实际值的差距。
train_predict = result_arma.predict()
train_predict = predict_recover(train_predict)
#还原RMSE = np.sqrt(((train_predict-timeseries)**2)
.sum()/timeseries.size)
9.预测未来的值
用statsmodel这个包来进行预测,很奇怪的是我从来没成功过,只能进行下一步(之后一天)的预测,多天的就无法做到了。这里提供他们的代码,供大家自行试验,成功的话一定要留言教我啊!跪谢。
predict_ts = result_arma.predict()
还有根据,用来预测的代码是:
for t in range(len(test)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test[t]
history.append(obs)
print('predicted=%f, expected=%f' % (yhat, obs))
forecast方法详细说明参见,
此外,Stackoverflow上的一个解答:,又给了一个预测的写法。
10. 更方便的时间序列包:pyflux
好在《》提到了python的另一个包pyflux,它的文档在。这个包在macOS上安装之前需要安装XCode命令行工具:
xcode-select --install
同时它的画图需要安装一个seaborn的包(如果没有Anaconda则用pip的方式。《》简要介绍了seaborn,它是“在matplotlib的基础上进行了更高级的API封装”。
conda install seaborn
我用这个包写了一个简略而完整的ARIMA建模:
http://www.pyflux.com/docs/arima.html
数据挖掘入门与实战
教你机器学习,教你数据挖掘