《深度学习入门》第7章实战:手写数字识别——卷积神经网络
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、一点介绍
-
- 1.整体结构
- 2.卷积层
-
- 卷积运算
- 填充
- 步幅
- 3.池化层
- 二、卷积层和池化层的实现
- 三、全部代码及运行结果
前言
最近阅读了《深度学习入门——基于Python的理论与实现》这本书的第7章,这一章主要讲解的是卷积神经网络。卷积神经网络(Convolutional Neural Network, CNN)可以被用于图像识别、语音识别的各种场合。
一、一点介绍
1.整体结构
和之前学习的神经网络相比,CNN多了一个卷积层(convolutional层)和一个池化层(pooling层)。
CNN 的层的连接顺序是“Convolution - ReLU -(Pooling)”(Pooling层有时会被省略)。这可以理解为之前的“Affine - ReLU”连接被替换成了“Convolution - ReLU -(Pooling)”连接。

2.卷积层
在全连接层中,数据都被拉平为1维的数据输入到网络中。所以说在全连接层中,数据的形状实际上是被忽视了的。但是卷积层可以保持数据的形状不变。
CNN 中,有时将卷积层的输入输出数据称为特征图(feature map)。其中,卷积层的输入数据称为输入特征图(input feature map),输出数据称为输出特征图(output feature map)。本书中将“输入输出数据”和“特征图”作为含义相同的词使用。
卷积运算
卷积运算包含的对象有输入数据和滤波器。(假设我们现在输入的是二维的数据,对应的滤波器也是二维的)

对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用。这里所说的窗口是指图7-4中灰色的3 × 3的部分。如图7-4所示,将各个位置上滤波器的元素和输入的对应元素相乘,然后再求和(有时将这个计算称为乘积累加运算)。然后,将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍,就可以得到卷积运算的输出。
在全连接的神经网络中,除了权重参数,还存在偏置。CNN中,滤波器的参数就对应之前的权重。并且,CNN中也存在偏置。图7-3的卷积运算的例子一直展示到了应用滤波器的阶段。包含偏置的卷积运算的处理流如图7-5所示。


填充
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比
如0等),这称为填充(padding)。
通过填充,大小为(4, 4)的输入数据变成了(6, 6)的形状。然后,应用大小为(3, 3)的滤波器,生成了大小为(4, 4)的输出数据。
这个例子中将填充设成了1,不过填充的值也可以设置成2、3等任意的整数。在图7-5的例子中,如果将填充设为2,则输入数据的大小变为(8, 8);如果将填充设为3,则大小变为(10, 10)。
使用填充主要是为了调整输出的大小。
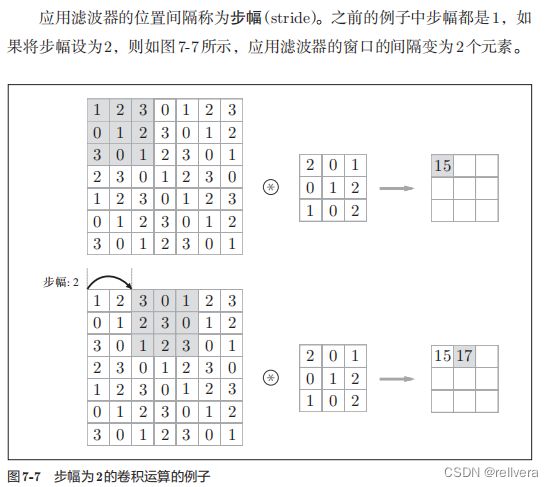
步幅
3.池化层
池化是缩小高、长方向上的空间的运算。通常来说池化分为两种:Max池化和Average池化。
Max池化:获取最大值。
Average池化:获取平均值。
下图中的例子是按照步幅2进行2*2的Max池化时的处理顺序。
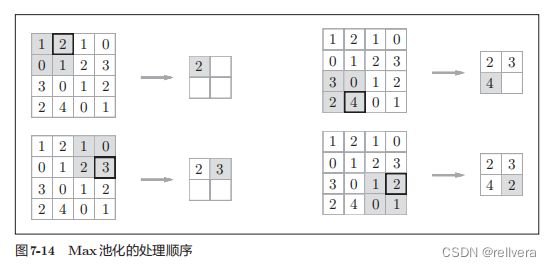
池化层的特征:
1.没有要学习的参数。
池化只是从目标区域中获取最大值或者平均值,不存在要学习的参数。
2.通道数不发生变化。
经过池化运算,输入数据和输出数据的通道数没有发生变化。如下图所示,计算是按照通道数独立进行的。

二、卷积层和池化层的实现
参考这篇博文:https://blog.csdn.net/LeungSr/article/details/127203161
三、全部代码及运行结果
from collections import OrderedDict
import sys, os
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from common.functions import *
from common.layers import *
from collections import OrderedDict
from dataset.mnist import load_mnist
from dataset.two_layer_net import TwoLayerNet
from common.trainer import Trainer
import pickle
class SimpleConvNet:
# input_dim 输入数据的尺寸,默认1通道,高28,长28
# filter_num 滤波器数量
# filter_size 滤波器大小
# pad 填充
# stride 步幅,默认为1
# hidden_size 隐藏层(全连接)中的神经元数量
# output_size 输出层(全连接)中的神经元数量
# weight_init_std 初始化时权重的标准差
def __init__(self, input_dim=(1,28,28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 初始化权重参数
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成必要的层
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x是输入数据,t是标签
def loss(self, x, t):
y = self.predict(x)
return self.last_layer.forward(y, t)
# 计算精确度
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1:
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i + 1)]
self.layers[key].b = self.params['b' + str(i + 1)]
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'] = self.layers['Conv1'].dW
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dW
grads['b2'] = self.layers['Affine1'].db
grads['W3'] = self.layers['Affine2'].dW
grads['b3'] = self.layers['Affine2'].db
return grads
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
# 处理花费时间较长的情况下减少数据
# x_train, t_train = x_train[:5000], t_train[:5000]
# x_test, t_test = x_test[:1000], t_test[:1000]
max_epochs = 20
network = SimpleConvNet(input_dim=(1, 28, 28),
conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
trainer.train()
# 保存参数
network.save_params("params.pkl")
print("Saved Network Parameters!")
# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()