Word2Vec原论文阅读
Word2Vec原论文阅读
一、背景
Word2Vec 是自然语言处理、文本表示学习的典型模型,首次提出了 CBOW、Skip-gram 等目前仍在沿用的词向量学习思想,也是除了预训练模型生成词向量之外,最具有代表性的神经网络词向量模型。直至目前,基于 Word2Vec 生成的词向量仍然在很多自然语言处理任务中得到使用。理解 Word2Vec 模型,对理解文本表示学习、词向量训练具有重要的意义。
Word2Vec 模型首次在2013年被 Tomas Mikolov 等人在《Efficient Estimation of Word Representations in Vector Space》论文被提出,该论文发表在深度学习领域顶会 ICLR。但是,该论文并没有详细描述 Word2Vec 的模型细节,重点在于讨论现有 NNLM 模型(神经网络语言模型)的时间复杂度,并从减少训练时间复杂度的角度出发提出了 CBOW 和 Skip-gram 思想。在此之后,Xin Rong 于2017年发表了论文《word2vec Parameter Learning Explained》,详细介绍了 Word2Vec 模型的内部机理和参数训练过程。
本文主要阅读并总结了 Word2Vec 原始论文《Efficient Estimation of Word Representations in Vector Space》,对该论文及其提出的 Word2Vec 模型进行了一个大致介绍,将在之后详细阅读并总结论文《word2vec Parameter Learning Explained》。
二、目的
在 Word2Vec 提出之前,主流的词向量表示法包括 one-hot 编码、词袋模型、N-gram 语言模型、NNLM 模型等,但上述模型存在两个共性问题:
① 词义相似度。不同词的词义一定有远近之分,例如 Queen 与 Women 的相似度一定大于同 Men 的相似度,理想的词向量应当能够表示这种词义相似度。
② 维度灾难。非神经网络模型存在的共同问题是词向量维度同词表大小正相关,词表扩张会带来词向量空间占用的倍增,而 NNLM 模型的计算复杂度也非常高。
针对以上两个问题,该论文提出了 Word2Vec 模型,分别在一定程度上解决了上述两个问题:
① 词义相似度。针对该问题,Tomas Mikolov 提出了词义相似度的判断标准,即词向量满足什么条件下视作能够反映词义相似度:通过向量间的运算能够找到指定条件的最近义词。同时,进一步提出了多种词义相似度,包括语义相似(例如 France 与 Italy 的相似)和语法相似(例如 Bigger 与 Smaller 的相似)。基于提出的多种相似度,构建了一个测试集及评测标准。
② 降低复杂度。针对该问题,作者采用了先使用简单模型训练词向量,进而使用词向量加入到下游任务训练的思想,去掉了 NNLM 的隐藏层来使用一个简单模型生成词向量,极大地减小了计算复杂度以使其能应用在大规模数据集上。
三、具体模型
本文搭建的具体模型是在 NNLM 模型的基础上去掉隐藏层,分别基于 CBOW 和 Skip-Gram 两种任务实现的。
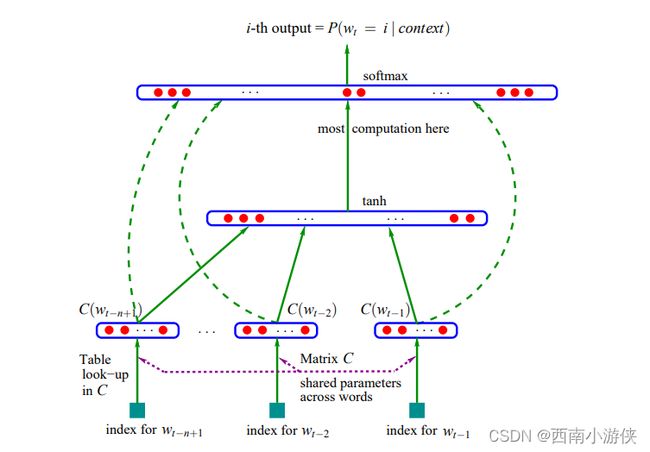
NNLM 模型的结构放在当下并不算复杂,就是非常典型的前馈神经网络:
和目前主流的概念不同的是,在 NNLM 论文中,将该网络分成了四层:输入层、投影层、隐藏层与输出层,其中的投影层是目前较为少见的概念,其实可以看作是隐藏层的第一层,用于将 one-hot 向量映射到低维稠密向量空间中。其主要是基于一个共享参数矩阵 P(D * V 维,其中 D 为设定的词向量维度,V 为词表大小),在投影层计算:
O u t p u t D × 1 = P D × V × I n p u t V × 1 Output_{D\times1} = P_{D\times V} \times Input_{V\times1} OutputD×1=PD×V×InputV×1
其中,Input 为输入层输入的 one-hot 编码,Output 为投影层输出(即隐藏层输入)。该操作实质上是根据 one-hot 编码选取对应维度下的参数矩阵值作为该输入的词向量。
后续的隐藏层即是经典的前馈神经网络结构,输入层为一个 SoftMax 分类器,输出前 n-1 个单词输入下第 n 个单词的概率分布(类似于 N-gram 语言模型)。
在 NNLM 的基础上,Word2Vec 进一步去掉了全连接的隐藏层以提升计算效率,即整体框架为输入层、投影层(现在一般称为隐藏层)、输出层,训练之后的投影层共享参数矩阵即为词向量的计算矩阵。
在简化模型的基础上,Tomas Mikolov 提出了两种训练任务以保证词向量的准确性,其一是连续词袋模型(Continuous Bag-of-Words Model ,CBOW),另一个是连续跳步模型(Continuous Skip-gram Model,Skip-gram):
① CBOW:其基本思想为输入上下文,预测中间单词。具体而言,设定一个上下文范围 N,输入为指定单词的前 N 个单词和后 N 个单词,输出为指定单词位置的概率分布,优化输出概率分布实现参数的优化。
② Skip-gram:其基本思想为基于中间单词,预测上下文。具体而言,同样设定一个上下文范围 N,输入为指定单词,输出为前 N 个单词和后 N 个单词的概率分布,做 2N 次分类的预测。
两者的基本思想图示如下:
基于这两种思想训练的 Word2Vec 模型在极大减少计算复杂度的基础上取得了良好的表示效果,事实上,直至目前 NLP 领域的热门模型 BERT,其同样使用了 CBOW 思想。
四、计算复杂度的讨论及效果
该论文因提出了 Word2Vec 模型而成为了 NLP 领域的里程碑,但在论文本体中,作者重点是讨论了计算复杂度并以此引申出来了 Word2Vec 模型。在此部分,我们简述论文中关于计算复杂度的讨论。
NNLM 模型计算得到的词向量效果在之前的词向量基础上是有所飞跃的,但是 NNLM 模型的计算复杂度极大,基于上文的模型架构,我们可以计算出 NNLM 的计算复杂度为:
Q = N × D + N × D × H + H × V Q = N \times D + N \times D \times H + H \times V Q=N×D+N×D×H+H×V
其中,N 为需要计算的前向词数量,D 为设定的词向量维度,H 为隐藏层维度,V 为词表大小。计算模型的复杂度为输入维度与输出维度的乘积来计算该层的参数量,上述公式分别是投影层(输出为 N * D ),隐藏层(输出为 H ),输出层(输出为 V )。根据上述公式,时间复杂度最高项本应在输出层(因为词表大小 V 一般为训练文本中的所有词的总数),但通过在输出层使用霍夫曼树编码,可以将输出层的复杂度从 V 降低到:
log 2 ( u n i g r a m ( V ) ) \log_2{(unigram(V))} log2(unigram(V))
因此,目前的最高时间复杂度出现在隐藏层,其计算复杂度远高于投影层和处理之后的输出层。因此,作者去掉了 NNLM 中的隐藏层,以大大降低了模型的计算复杂度。在去掉隐藏层之后,Word2Vec 的两种任务分别的计算复杂度为:
① CBOW:
Q = N × D + D × l o g 2 V Q = N \times D + D \times log_2V Q=N×D+D×log2V
其中各变量的指代与上式相同,由于去掉了隐藏层,输出层的输入即为词向量维度 D。
② Skip-gram:
Q = C × ( D + D × l o g 2 V ) Q = C \times (D + D \times log_2V) Q=C×(D+D×log2V)
在 Skip-gram 中的计算复杂度同 NNLM 略有不同。C 为选定上下文范围之和(2N),即做 C 次分类任务,每次任务中,由于仅输入一个单词,因此取 N = 1,即投影层的输出为 1 * D 维。
从上述计算复杂度公式可以看出,Word2Vec 极大地减少了计算复杂度,同时,通过提出的两种预测任务,确保了预测准确性。事实上,由于 NNLM 的计算复杂度较高,其不适合在海量文本数据集上进行文本表示训练。在论文中,作者在多个公共数据集上进行了训练并使用其提出的多维词义相似度测试集进行测试,Word2Vec 相比于传统 NNLM 和改进的 RNNLM(循环神经网络语言模型)都有更为优越的相似度计算表现以及时间成本,证明了 Word2Vec 的优越性。
五、词义相似度衡量
除去提出上述模型之外,作者也基于词义相似度的考虑,提出了一个多维词义相似度测试数据集,具体的,定义了以下五种词义相似度和九种语法相似度:
在该数据集进行测试的具体过程为:将不同单词进行随机配对生成数万个词对,基于类似于:
X = v e c t o r ( b i g g e s t ) − v e c t o r ( b i g ) + v e c t o r ( s m a l l ) X = vector(biggest) - vector(big) + vector(small) X=vector(biggest)−vector(big)+vector(small)
的公式计算出 smallest 单词的对应词向量,再词库中查找目标词向量 X 距离最近的词向量是否是 smallest 单词对应词向量,即可通过准确率判断模型在该测试集上的测试效果。