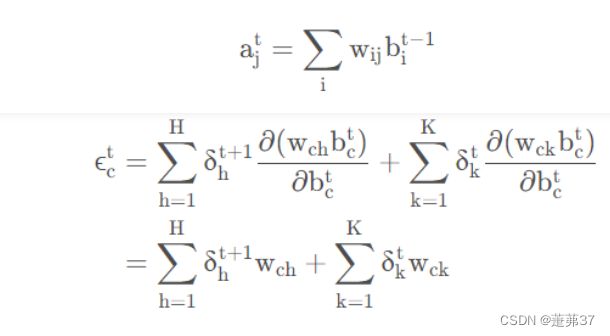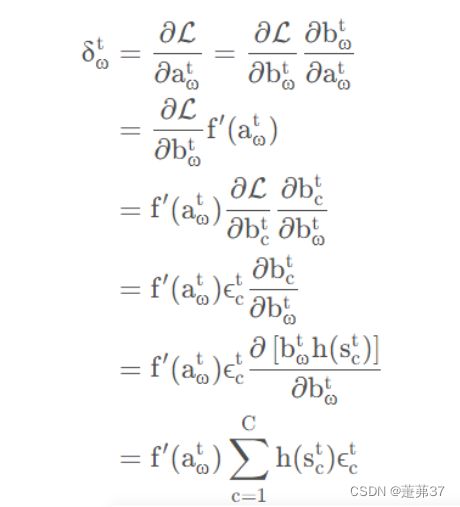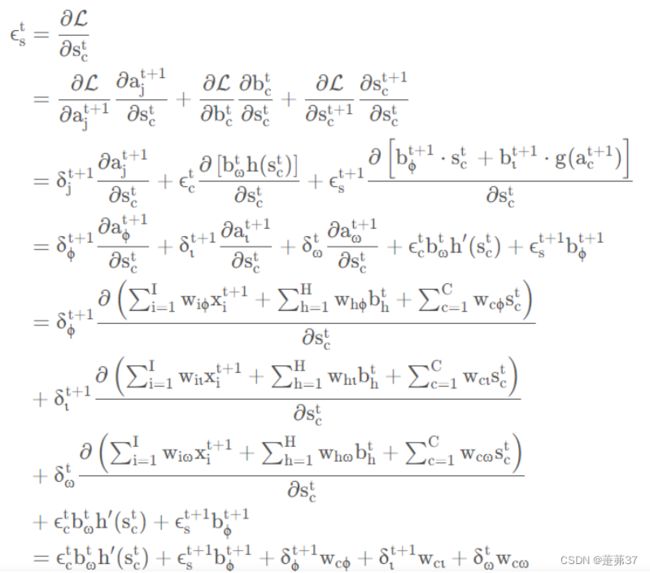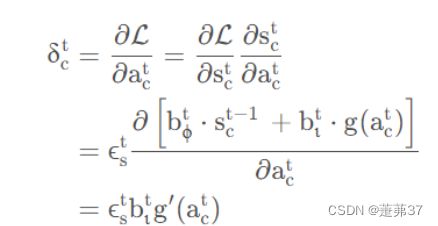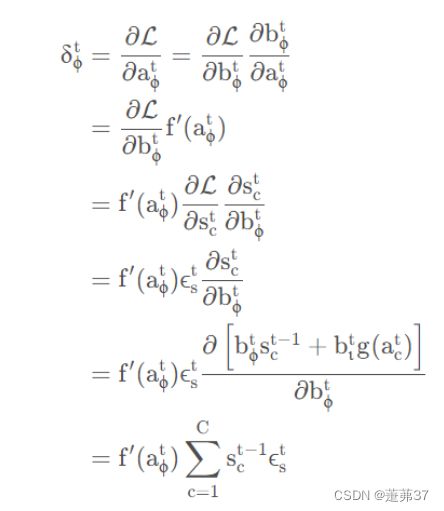NNDL 作业10：第六章课后题（LSTM | GRU）
文章目录
-
- 习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决办法.
- 习题6-4 推导LSTM网络中参数的梯度，并分析其避免梯度消失的效果编辑
- 习题6-5 推导GRU网络中参数的梯度，并分析其避免梯度消失的效果编辑
- 附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?
- 附加题 6-2P LSTM BP推导，并用Numpy实现
- 总结
- 参考
习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决办法.
公式(6.50)为： h t = h t − 1 + g ( x t , h t − 1 ; Θ ) h_{t}=h_{t-1}+g(x_{t},h_{t-1};\Theta ) ht=ht−1+g(xt,ht−1;Θ)
原因：在计算误差项时，可能会出现梯度过大的情况。
解决办法：使用长短期记忆神经网络。
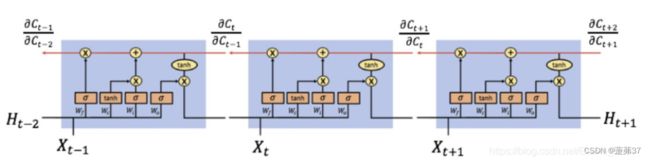
习题6-4 推导LSTM网络中参数的梯度，并分析其避免梯度消失的效果编辑
LSTM的结构如下：
3.Cell状态（长时记忆）
4.Cell输出（短时记忆）
5.遗忘门
6.输入门
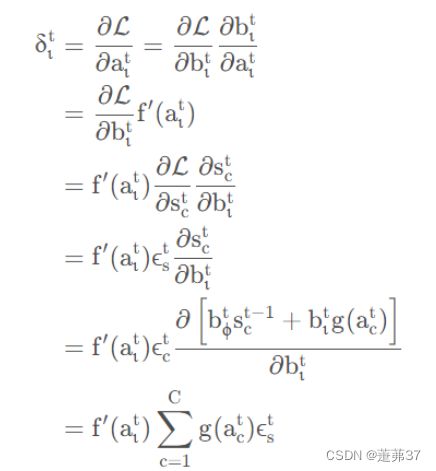避免梯度消失的效果：LSTM把原本RNN的单元改造成一个叫做CEC的部件，这个部件保证了误差将以常数的形式在网络中流动 ，并在此基础上添加输入门和输出门使得模型变成非线性的，并可以调整不同时序的输出对模型后续动作的影响，因此可以一定程度上克服梯度消失问题。
习题6-5 推导GRU网络中参数的梯度，并分析其避免梯度消失的效果编辑
GRU它引⼊了重置门（reset gate）和更新门（update gate) 的概念，从而修改了循环神经⽹络中隐藏状态的计算⽅式。GRU的优点是这是个更加简单的模型，所以更容易创建一个更大的网络，而且它只有两个门，在计算性上也运行得更快，然后它可以扩大模型的规模。
附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?
GRU和LSTM的区别在于：
①GRU通过更新门来控制上一时刻的信息传递和当前时刻计算的隐层信息传递。GRU中由于是一个参数进行控制，因而可以选择完全记住上一时刻而不需要当前计算的隐层值，或者完全选择当前计算的隐层值而忽略上一时刻的所有信息，最后一种情况就是无论是上一时刻的信息还是当前计算的隐层值都选择传递到当前时刻隐层值，只是选择的比重不同。而LSTM是由两个参数（遗忘门和输入门）来控制更新的，他们之间并不想GRU中一样只是由一个参数控制，因而在比重选择方面跟GRU有着很大的区别，例如它可以既不选择上一时刻的信息，也不选择当前计算的隐层值信息（输入门拒绝输入，遗忘门选择遗忘）。
②GRU要在上一时刻的隐层信息的基础上乘上一个重置门，而LSTM无需门来对其控制，LSTM必须考虑上一时刻的隐层信息对当前隐层的影响，而GRU则可选择是否考虑上一时刻的隐层信息对当前时刻的影响。
③ 一般来说两者效果差不多，性能在很多任务上也不分伯仲。GRU参数更少，收敛更快；数据量很大时，LSTM效果会更好一些，因为LSTM参数也比GRU参数多一些。
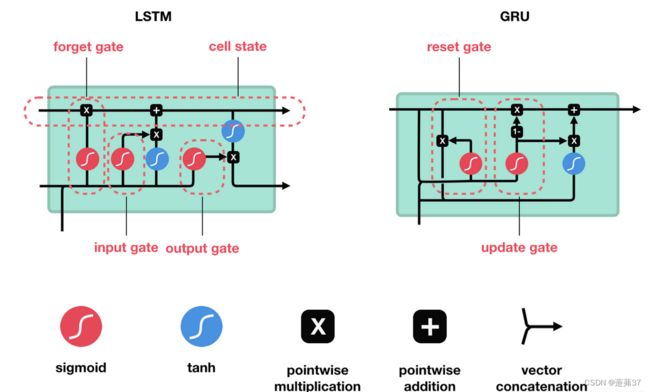GRU 和 LSTM 的对比
- GRU 是 LSTM 变动较大的变体
- LSTM 能够解决循环神经网络因长期依赖带来的梯度消失和梯度爆炸问题，但是 LSTM 有三个不同的门，参数较多，训练起来比较困难。GRU
只含有两个门控结构，且在超参数全部调优的情况下，二者性能相当，但是 GRU 结构更为简单，训练样本较少，易实现。
GRU 在 LSTM 的基础上主要做出了两点改变：
-
GRU 只有两个门。GRU 将 LSTM 中的输入门和遗忘门合二为一，称为更新门（updategate），下图中的z(t)，控制前边记忆信息能够继续保留到当前时刻的数据量，或者说决定有多少前一时间步的信息和当前时间步的信息要被继续传递到未来；GRU 的另一个门称为重置门（reset gate），下图中的r(t)，控制要遗忘多少过去的信息。
-
取消进行线性自更新的记忆单元（memory cell），而是直接在隐藏单元中利用门控直接进行线性自更新。GRU 的逻辑图如下图所示。
-
利用重置门重置记忆信息
GRU 不再使用单独的记忆细胞存储记忆信息，而是直接利用隐藏单元记录历史状态。利用重置门控制当前信息和记忆信息的数据量，并生成新的记忆信息继续向前传递。 -
利用更新门计算当前时刻隐藏状态的输出 隐藏状态的输出信息由前一时刻的隐藏状态信息h_(t-1)和当前时刻的隐藏状态输出h_t
，利用更新门控制这两个信息传递到未来的数据量。
分别对应下图的四个公式
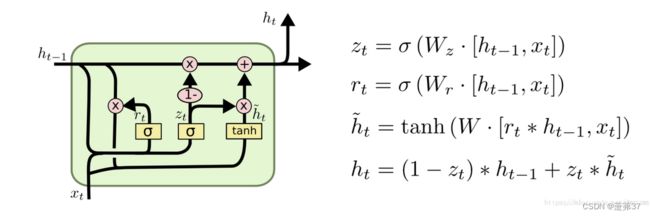
GRU 输入输出的结构与普通的 RNN 相似，其中的内部思想与 LSTM 相似。与 LSTM 相比，GRU 内部少了一个”门控“，参数比LSTM 少，但是却也能够达到与 LSTM 相当的功能。考虑到硬件的计算能力和时间成本，因而很多时候我们也就会选择更加“实用的 ”GRU 。
附加题 6-2P LSTM BP推导，并用Numpy实现
import numpy as np
import torch
def sigmoid(x):
return 1 / (1 + np.exp(-x))
class LSTMCell:
def __init__(self, weight_ih, weight_hh, bias_ih, bias_hh):
self.weight_ih = weight_ih
self.weight_hh = weight_hh
self.bias_ih = bias_ih
self.bias_hh = bias_hh
self.dc_prev = None
self.dh_prev = None
self.weight_ih_grad_stack = []
self.weight_hh_grad_stack = []
self.bias_ih_grad_stack = []
self.bias_hh_grad_stack = []
self.x_stack = []
self.dx_list = []
self.dh_prev_stack = []
self.h_prev_stack = []
self.c_prev_stack = []
self.h_next_stack = []
self.c_next_stack = []
self.input_gate_stack = []
self.forget_gate_stack = []
self.output_gate_stack = []
self.cell_memory_stack = []
def __call__(self, x, h_prev, c_prev):
a_vector = np.dot(x, self.weight_ih.T) + np.dot(h_prev, self.weight_hh.T)
a_vector += self.bias_ih + self.bias_hh
h_size = np.shape(h_prev)[1]
a_i = a_vector[:, h_size * 0:h_size * 1]
a_f = a_vector[:, h_size * 1:h_size * 2]
a_c = a_vector[:, h_size * 2:h_size * 3]
a_o = a_vector[:, h_size * 3:]
input_gate = sigmoid(a_i)
forget_gate = sigmoid(a_f)
cell_memory = np.tanh(a_c)
output_gate = sigmoid(a_o)
c_next = (forget_gate * c_prev) + (input_gate * cell_memory)
h_next = output_gate * np.tanh(c_next)
self.x_stack.append(x)
self.h_prev_stack.append(h_prev)
self.c_prev_stack.append(c_prev)
self.c_next_stack.append(c_next)
self.h_next_stack.append(h_next)
self.input_gate_stack.append(input_gate)
self.forget_gate_stack.append(forget_gate)
self.output_gate_stack.append(output_gate)
self.cell_memory_stack.append(cell_memory)
self.dc_prev = np.zeros_like(c_next)
self.dh_prev = np.zeros_like(h_next)
return h_next, c_next
def backward(self, dh_next):
x_stack = self.x_stack.pop()
h_prev = self.h_prev_stack.pop()
c_prev = self.c_prev_stack.pop()
c_next = self.c_next_stack.pop()
input_gate = self.input_gate_stack.pop()
forget_gate = self.forget_gate_stack.pop()
output_gate = self.output_gate_stack.pop()
cell_memory = self.cell_memory_stack.pop()
dh = dh_next + self.dh_prev
d_tanh_c = dh * output_gate * (1 - np.square(np.tanh(c_next)))
dc = d_tanh_c + self.dc_prev
dc_prev = dc * forget_gate
self.dc_prev = dc_prev
d_input_gate = dc * cell_memory
d_forget_gate = dc * c_prev
d_cell_memory = dc * input_gate
d_output_gate = dh * np.tanh(c_next)
d_ai = d_input_gate * input_gate * (1 - input_gate)
d_af = d_forget_gate * forget_gate * (1 - forget_gate)
d_ao = d_output_gate * output_gate * (1 - output_gate)
d_ac = d_cell_memory * (1 - np.square(cell_memory))
da = np.concatenate((d_ai, d_af, d_ac, d_ao), axis=1)
dx = np.dot(da, self.weight_ih)
dh_prev = np.dot(da, self.weight_hh)
self.dh_prev = dh_prev
self.dx_list.insert(0, dx)
self.dh_prev_stack.append(dh_prev)
self.weight_ih_grad_stack.append(np.dot(da.T, x_stack))
self.weight_hh_grad_stack.append(np.dot(da.T, h_prev))
db = np.sum(da, axis=0)
self.bias_ih_grad_stack.append(db)
self.bias_hh_grad_stack.append(db)
return dh_prev
np.random.seed(123)
torch.random.manual_seed(123)
np.set_printoptions(precision=6, suppress=True)
lstm_torch = torch.nn.LSTMCell(2, 3).double()
lstm_numpy = LSTMCell(lstm_torch.weight_ih.data.numpy(),
lstm_torch.weight_hh.data.numpy(),
lstm_torch.bias_ih.data.numpy(),
lstm_torch.bias_hh.data.numpy())
x_numpy = np.random.random((4, 2))
x_torch = torch.tensor(x_numpy, requires_grad=True)
h_numpy = np.random.random((4, 3))
h_torch = torch.tensor(h_numpy, requires_grad=True)
c_numpy = np.random.random((4, 3))
c_torch = torch.tensor(c_numpy, requires_grad=True)
dh_numpy = np.random.random((4, 3))
dh_torch = torch.tensor(dh_numpy, requires_grad=True)
h_numpy, c_numpy = lstm_numpy(x_numpy, h_numpy, c_numpy)
h_torch, c_torch = lstm_torch(x_torch, (h_torch, c_torch))
h_torch.backward(dh_torch)
dh_numpy = lstm_numpy.backward(dh_numpy)
print("h_numpy :\n", h_numpy)
print("h_torch :\n", h_torch.data.numpy())
print("---------------------------------")
print("c_numpy :\n", c_numpy)
print("c_torch :\n", c_torch.data.numpy())
print("---------------------------------")
print("dx_numpy :\n", np.sum(lstm_numpy.dx_list, axis=0))
print("dx_torch :\n", x_torch.grad.data.numpy())
print("---------------------------------")
print("w_ih_grad_numpy :\n",
np.sum(lstm_numpy.weight_ih_grad_stack, axis=0))
print("w_ih_grad_torch :\n",
lstm_torch.weight_ih.grad.data.numpy())
print("---------------------------------")
print("w_hh_grad_numpy :\n",
np.sum(lstm_numpy.weight_hh_grad_stack, axis=0))
print("w_hh_grad_torch :\n",
lstm_torch.weight_hh.grad.data.numpy())
print("---------------------------------")
print("b_ih_grad_numpy :\n",
np.sum(lstm_numpy.bias_ih_grad_stack, axis=0))
print("b_ih_grad_torch :\n",
lstm_torch.bias_ih.grad.data.numpy())
print("---------------------------------")
print("b_hh_grad_numpy :\n",
np.sum(lstm_numpy.bias_hh_grad_stack, axis=0))
print("b_hh_grad_torch :\n",
lstm_torch.bias_hh.grad.data.numpy())
运行结果：
h_numpy :
[[ 0.055856 0.234159 0.138457]
[ 0.094461 0.245843 0.224411]
[ 0.020396 0.086745 0.082545]
[-0.003794 0.040677 0.063094]]
h_torch :
[[ 0.055856 0.234159 0.138457]
[ 0.094461 0.245843 0.224411]
[ 0.020396 0.086745 0.082545]
[-0.003794 0.040677 0.063094]]
---------------------------------
c_numpy :
[[ 0.092093 0.384992 0.213364]
[ 0.151362 0.424671 0.318313]
[ 0.033245 0.141979 0.120822]
[-0.0061 0.062946 0.094999]]
c_torch :
[[ 0.092093 0.384992 0.213364]
[ 0.151362 0.424671 0.318313]
[ 0.033245 0.141979 0.120822]
[-0.0061 0.062946 0.094999]]
---------------------------------
dx_numpy :
[[-0.144016 0.029775]
[-0.229789 0.140921]
[-0.246041 -0.009354]
[-0.088844 0.036652]]
dx_torch :
[[-0.144016 0.029775]
[-0.229789 0.140921]
[-0.246041 -0.009354]
[-0.088844 0.036652]]
---------------------------------
w_ih_grad_numpy :
[[-0.056788 -0.036448]
[ 0.018742 0.014428]
[ 0.007827 0.024828]
[ 0.07856 0.05437 ]
[ 0.061267 0.045952]
[ 0.083886 0.0655 ]
[ 0.229755 0.156008]
[ 0.345218 0.251984]
[ 0.430385 0.376664]
[ 0.014239 0.011767]
[ 0.054866 0.044531]
[ 0.04654 0.048565]]
w_ih_grad_torch :
[[-0.056788 -0.036448]
[ 0.018742 0.014428]
[ 0.007827 0.024828]
[ 0.07856 0.05437 ]
[ 0.061267 0.045952]
[ 0.083886 0.0655 ]
[ 0.229755 0.156008]
[ 0.345218 0.251984]
[ 0.430385 0.376664]
[ 0.014239 0.011767]
[ 0.054866 0.044531]
[ 0.04654 0.048565]]
---------------------------------
w_hh_grad_numpy :
[[-0.037698 -0.048568 -0.021069]
[ 0.016749 0.016277 0.007556]
[ 0.035743 0.02156 0.000111]
[ 0.060824 0.069505 0.029101]
[ 0.060402 0.051634 0.025643]
[ 0.068116 0.06966 0.035544]
[ 0.168965 0.217076 0.075904]
[ 0.248277 0.290927 0.138279]
[ 0.384974 0.401949 0.167006]
[ 0.015448 0.0139 0.005158]
[ 0.057147 0.048975 0.022261]
[ 0.057297 0.048308 0.017745]]
w_hh_grad_torch :
[[-0.037698 -0.048568 -0.021069]
[ 0.016749 0.016277 0.007556]
[ 0.035743 0.02156 0.000111]
[ 0.060824 0.069505 0.029101]
[ 0.060402 0.051634 0.025643]
[ 0.068116 0.06966 0.035544]
[ 0.168965 0.217076 0.075904]
[ 0.248277 0.290927 0.138279]
[ 0.384974 0.401949 0.167006]
[ 0.015448 0.0139 0.005158]
[ 0.057147 0.048975 0.022261]
[ 0.057297 0.048308 0.017745]]
---------------------------------
b_ih_grad_numpy :
[-0.084682 0.032588 0.046412 0.126449 0.111421 0.139337 0.361956
0.539519 0.761838 0.027649 0.103695 0.099405]
b_ih_grad_torch :
[-0.084682 0.032588 0.046412 0.126449 0.111421 0.139337 0.361956
0.539519 0.761838 0.027649 0.103695 0.099405]
---------------------------------
b_hh_grad_numpy :
[-0.084682 0.032588 0.046412 0.126449 0.111421 0.139337 0.361956
0.539519 0.761838 0.027649 0.103695 0.099405]
b_hh_grad_torch :
[-0.084682 0.032588 0.046412 0.126449 0.111421 0.139337 0.361956
0.539519 0.761838 0.027649 0.103695 0.099405]
Process finished with exit code 0
总结
这次作业和上次作业有密切联系，公式推导参考同学的才推导出来，对我来说还是有难度的。了解到GRU 输入输出的结构与普通的 RNN 相似，其中的内部思想与 LSTM 相似。与 LSTM 相比，GRU 内部少了一个”门控“，参数比LSTM 少，但是却也能够达到与 LSTM 相当的功能。考虑到硬件的计算能力和时间成本，因而很多时候我们也就会选择更加“实用”的 GRU 。
参考
深度学习笔记-目录 (ai-start.com)
GRU和LSTM区别
GRU 和 LSTM 的对比