矩阵分解算法

0 前言

在协同过滤算法中 我们知道近邻协同过滤算法的显著缺点：

• 没有充分利用物品本身的属性信息
• 处理稀疏矩阵能力很弱，泛化能力很弱

为了解决以上问题，引入了基于矩阵分解（Matrix Factorization,MF）的协同过滤算法

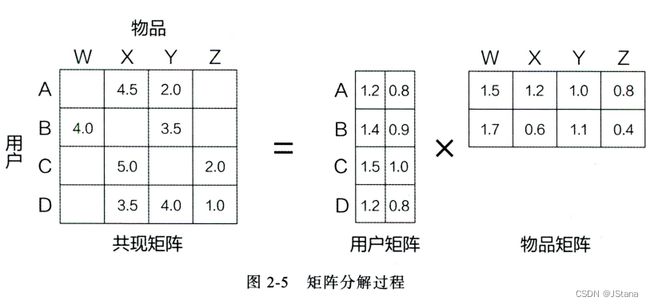
矩阵分解协同过滤算法：通过矩阵分解的方式将用户物品共线矩阵实现降维，从而泛化预测 用户物品未知位置的评分

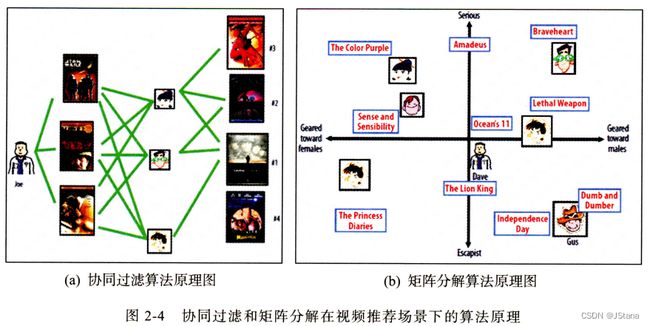
下图是《深度学习推荐系统》中的协同过滤算法与矩阵分解算法在推荐场景下的原理比较

协同过滤算法找到用户可能喜欢的视频的方式很直接，即基于用户的观看历史，找到跟目标用户看过同样视频的相似用户，然后找到这些相似用户喜欢看的其他视频，推荐给目标用户。

矩阵分解算法则期望为每一个用户和视频生成一个隐向量，将用户和视频定位到隐向量的表示空间上(如图 2-4(b)所示)，距离相近的用户和视频表明兴趣特点接近，在推荐过程中，就应该把距离相近的视频推荐给目标用户。例如，如果希望为图 2-4(b)中的用户 Dave 推荐视频，可以发现离 Dave 的用户向量最近的两个视频向量分别是“Ocean’s 11”和“The Lion King”，那么可以根据向量距离由近到远的顺序生成 Dave 的推荐列表。

最初的思路是利用SVD矩阵分解，然后到**LFM隐语义（因子）**模型。到现在这一类的模型被叫做 交替最小二乘（Alternating Least Squares， ALS）已经变成最优化的方法了。

1. 矩阵分解原理

对矩阵进行矩阵分解的主要方法有三种:

1. 特征值分解 Eigen Decomposition) ，只能作用于方阵，显然不适用于分解用户-物品矩阵
2. 奇异值分解 ( Singular Value Decomposition，SVD )
3. 梯度下降 ( GradientDescent)

相比特征值分解的要求矩阵是方阵，SVD 更具有普适性，在SLAM中应用广泛。这里我们只简单介绍一下它的表示含义
$$A=U\Sigma V^T$$

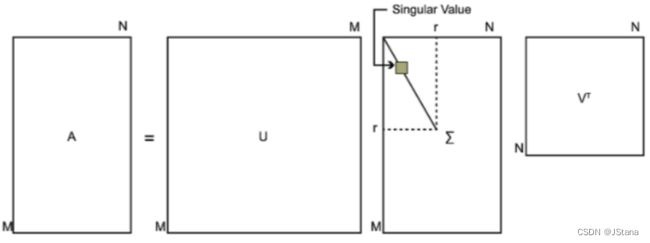
矩阵 $Am\times n$ ：m可以表示用户；n可以表示物品

矩阵 $Um\times m$

矩阵 $\Sigma m\times n$: 除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值

矩阵 $ V m × n $:U和V都是酉矩阵，即满足$U^TU=I,VTV=I$

大家只要知道 SVD的分解形式 有了解就可以 具体数学推导可以参考(奇异值分解(SVD)

代码实现

# 奇异值分解
np.linalg.svd(a, full_matrices=True, compute_uv=True)

# 参数
a : 是一个形如(M,N)矩阵

full_matrices：的取值是为0或者1，默认值为1，这时u的大小为(M,M)，v的大小为(N,N) 。否则u的大小为(M,K)，v的大小为(K,N) ，K=min(M,N)

compute_uv：取值是为0或者1，默认值为1，表示计算u,s,v。为0的时候只计算s


# 返回值： 总共有三个返回值u,s,v
其中s是对矩阵a的奇异值分解。s除了对角元素不为0，其他元素都为0，并且对角元素从大到小排列。s中有n个奇异值，一般排在后面的比较接近0，所以仅保留比较大的r个奇异值

从上面不难发现这种传统的SVD分解方式要求 A必须是稠密的，但是在推荐领域数据更多的是稀疏数据，如果用奇异值分解就必须将缺失值填充，而一旦补全， 空间复杂度就会非常高。 同时SVD分解计算复杂度非常高， 用户-物品矩阵非常大，这个开销是非常大的。

所以我们需要更好的分解方式，接下来我们介绍 隐因子模型（LFM）及其变型

1.1 LFM

2006年的Netflix Prize之后， Simon Funk公布了一个矩阵分解算法叫做Funk-SVD, 后来被Netflix Prize的冠军Koren称为Latent Factor Model(LFM)，Basic SVD 也是它

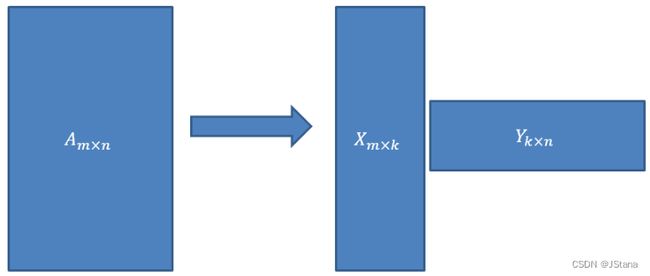
LFM（Latent Factor Model） 是在用户和物品的共现矩阵上，引入隐向量，用隐向量表示用户和物品，增强模型表征稀疏数据的能力,本质仍然是 矩阵分解算法，用一个图来表示：

$$A_{m\times n}=X_{m\times k}{Y}_{k\times n}$$

其将 m × n 的共现矩阵（m个用户；n个物品） 分解为：

• m × k 的用户向量矩阵
• k × n 的物品向量矩阵

k 表示隐向量的长度

• k 越小，隐向量越短，其包含的信息越少，模型的泛化能力越强；
• k 越大，隐向量越长，其包含的信息越多，模型的泛化能力越弱；
• k 的取值，还是要考量计算复杂度（长度约长，复杂度越大）以及实际场景中模型的效果

我们现在为什么把LFM及其变型当做ALS呢？

主要因为 我们 把求解上面两个矩阵的参数问题转换成一个最优化问题， 可以通过训练集里面的观察值利用最小化来学习用户矩阵和物品矩阵

直观案例展示

公式推导

表示形式 以上面 用户-物品为例
$$P^{LFM}(u,i)=\sum _{k=1}^k{p}_{uk}{q}_{ik}$$

LFM损失函数

显然我们预测的值和真实值是有误差的，那我们就要最小化这个误差
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲Loss &= \sum_{u…

加入L2正则化：
$$Loss=\sum _{u,i\in R}(r_{ui}-{\sum _{k=1}}^k{p}_{uk}{q}_{ik}{)}^2+\lambda (\sum _U{p_{uk}}^2+\sum _I{q_{ik}}^2)$$
对损失函数求偏导：
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲ \cfrac {\parti…

梯度下降更新参数$p_{uk}$：（梯度下降比较好理解，其他优化算法同理）
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲ p_{uk}&:=p_{uk…
同理：
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲ q_{ik}&:=q_{ik…
随机梯度下降： 向量乘法 每一个分量相乘 求和
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲ &p_{uk}:=p_{uk…
由于P矩阵和Q矩阵是两个不同的矩阵，通常分别采取不同的正则参数，${\lambda }_1$和${\lambda }_2$

不难看出 这就和训练模型的思路一致， 我们拿到了一个用户物品的评分矩阵， 而我们要去计算两个参数矩阵U和V

1. 初始化这两个矩阵：用户-隐变量矩阵，物品-隐变量矩阵
2. 把用户评分矩阵里面已经评过分的那些样本当做训练集的label， 把对应的用户和物品的隐向量当做features， 这样就会得到(features, label)相当于训练集
3. 通过两个隐向量乘积得到预测值pred
4. 根据label和pred计算损失
5. 然后反向传播， 通过梯度下降的方式，更新两个隐向量的值
6. 未评过分的那些样本当做测试集， 通过两个隐向量就可以得到测试集的label值
7. 这样就填充完了矩阵， 下一步就可以进行推荐了

算法关键代码实现

'''
LFM Model  
'''
import pandas as pd
import numpy as np

class LFM():

    def __init__(self, alpha, reg_p, reg_q, k=10, epochs=10, columns=["uid", "iid", "rating"]):
        self.alpha = alpha # 学习率
        self.reg_p = reg_p    # P矩阵正则
        self.reg_q = reg_q    # Q矩阵正则
        self.k = k  # 隐式类别数量
        self.epochs = epochs    # 最大迭代次数
        self.columns = columns

    def fit(self, dataset):
        '''
        fit dataset
        :param dataset: uid, iid, rating
        :return:
        '''

        self.dataset = pd.DataFrame(dataset)

        self.users_ratings = dataset.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]]
        self.items_ratings = dataset.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]]

        self.globalMean = self.dataset[self.columns[2]].mean()

        self.P, self.Q = self.sgd()

    def _init_matrix(self):
        '''
        初始化P和Q矩阵，同时为设置0，1之间的随机值作为初始值
        :return:
        '''
        # User-LF
        P = dict(zip(
            self.users_ratings.index,
            np.random.rand(len(self.users_ratings), self.k).astype(np.float32)
        ))
        # Item-LF
        Q = dict(zip(
            self.items_ratings.index,
            np.random.rand(len(self.items_ratings), self.k).astype(np.float32)
        ))
        return P, Q

    def sgd(self):
        '''
        使用随机梯度下降，优化结果
        :return:
        '''
        P, Q = self._init_matrix()

        for i in range(self.number_epochs):
            print("iter%d"%i)
            error_list = []
            for uid, iid, r_ui in self.dataset.itertuples(index=False):
                v_pu = P[uid] #用户向量
                v_qi = Q[iid] #物品向量
                err = np.float32(r_ui - np.dot(v_pu, v_qi))

                v_pu += self.alpha * (err * v_qi - self.reg_p * v_pu)
                v_qi += self.alpha * (err * v_pu - self.reg_q * v_qi)
                
                P[uid] = v_pu 
                Q[iid] = v_qi


                error_list.append(err ** 2)
            print(np.sqrt(np.mean(error_list)))
        return P, Q
    
        def predict(self, uid, iid):
        # 如果uid或iid不在，我们使用平均分作为预测结果返回
        if uid not in self.users_ratings.index or iid not in self.items_ratings.index:
            return self.globalMean

        p_u = self.P[uid]
        q_i = self.Q[iid]

        return np.dot(p_u, q_i)

    def test(self,testset):
        '''预测测试集数据'''
        for uid, iid, real_rating in testset.itertuples(index=False):
            try:
                pred_rating = self.predict(uid, iid)
            except Exception as e:
                print(e)
            else:
                yield uid, iid, real_rating, pred_rating
if __name__ == '__main__':
    dtype = [("userId", np.int32), ("movieId", np.int32), ("rating", np.float32)]
    dataset = pd.read_csv("data.csv", usecols=range(3), dtype=dict(dtype))

    lfm = LFM(0.02, 0.01, 0.01, 10, 100, ["userId", "movieId", "rating"])
    lfm.fit(dataset)

    while True:
        uid = input("uid: ")
        iid = input("iid: ")
        print(lfm.predict(int(uid), int(iid)))

1.2 BiasSVD

在FunkSVD提出来之后，出现了很多变形版本，其中一个相对成功的方法是BiasSVD，顾名思义，即带有偏置项的SVD分解：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QvNkt6Cq-1669452545098)(1. LFM算法.assets/矩阵分解4.jpg)]

它基于的假设和Baseline基准预测是一样的，但这里将Baseline的偏置引入到了矩阵分解中

1.3 SVD++

人们后来又提出了改进的BiasSVD，被称为SVD++，该算法是在BiasSVD的基础上添加了用户的隐式反馈信息：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HvVvjpfQ-1669452545099)(1. LFM算法.assets/矩阵分解5.jpg)]

显示反馈指的用户的评分这样的行为，隐式反馈指用户的浏览记录、购买记录、收听记录等。

SVD++是基于这样的假设：在BiasSVD基础上，认为用户对于项目的历史浏览记录、购买记录、收听记录等可以从侧面反映用户的偏好。

在参考5中实现了更多SVDs, 我也将会持续学习…更新会继续整理，最近整理一下数据，重新实现算法

参考

王喆 《深度学习推荐系统》

奇异值分解(SVD)原理与在降维中的应用 - 刘建平

ALS算法介绍（协同过滤算法介绍

隐语义模型(LFM)和矩阵分解(MF)

SVD在推荐系统中的应用详解以及算法推导