矩阵分解算法与因子分解机

矩阵分解

核心思想

矩阵分解的目的是通过机器学习的手段将用户行为矩阵中缺失的数据(用户没有评分的元素)填补完整，最终达到可以为用户做推荐的目标。
在推荐系统中，用户操作行为可以转化为如下的用户行为矩阵。
用户对标的物的操作行为矩阵矩阵分解算法是将用户评分矩阵分解为两个矩阵的乘积。

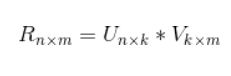
其中U，代表的用户特征矩阵，V代表标的物特征矩阵。某个用户对某个标的物的评分，就可以采用矩阵U对应的行(该用户的特征向量)与矩阵V对应的列(该标的物的特征向量)的乘积。有了用户对标的物的评分就很容易为用户做推荐了。具体，可以采用如下方式为用户做推荐：首先可以将用户特征向量

乘以标的物特征矩阵V，最终得到用户对每个标的物的评分.

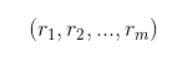
即：

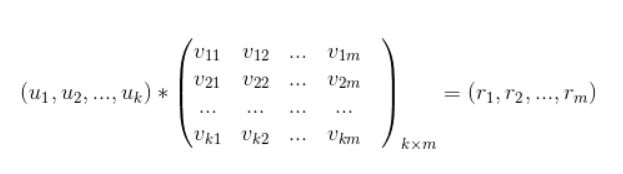
从该评分中过滤掉用户已经操作过的标的物，针对剩下的标的物得分做降序排列取topN推荐给用户。矩阵分解算法的核心思想是将用户行为矩阵分解为两个低秩矩阵的乘积，通过分解，我们分别将用户和标的物嵌入到了同一个k维的向量空间(k一般很小，几十到上百)，用户向量和标的物向量的内积代表了用户对标的物的偏好度。所以，矩阵分解算法本质上也是一种嵌入方法。

应用场景

1.应用于完全个性化推荐场景(完全个性化推荐范式)
2.应用于标的物关联标的物场景(标的物关联标的物范式)
3.用于用户及标的物聚类
4.应用于群组个性化场景(群组个性化推荐范式)

优缺点

1.优点
矩阵分解算法作为一类特殊的协同过滤算法，具备协同过滤算法的所有优点，具体表现在：

(1) 不依赖用户和标的物的其他信息，只需要用户行为就可以为用户做推荐
矩阵分解算法也是一类协同过滤算法，它只需要用户行为就可以为用户生成推荐结果，而不需要用户或者标的物的其他信息，而这类其他信息往往是半结构化或者非结构化的信息，不易处理，有时也较难获得。矩阵分解是领域无关的一类算法，因此，该优点可以让矩阵分解算法基本可以应用于所有推荐场景中，这也是矩阵分解算法在工业界大受欢迎的重要原因。

(2) 推荐精准度不错
矩阵分解算法是Netflix推荐大赛中获奖算法中非常重要的一类算法，准确度是得到业界一致认可和验证的，我们公司推荐业务中也大量利用矩阵分解算法，效果也是非常不错的。

(3) 可以为用户推荐惊喜的标的物
协同过滤算法利用群体的智慧来为用户推荐，具备为用户推荐差异化、有惊喜度的标的物的能力，矩阵分解算法作为协同过滤算法中一类基于隐因子的算法，当然也具备这个优点，甚至比user-based和item-based协同过滤算法有更好的效果。

(4) 易于并行化处理
矩阵分解是非常容易并行化的，Spark MLlib中就是采用ALS算法分布式进行矩阵分解的。

2.缺点
上面讲了这么多矩阵分解算法的优点，除了这些优点外，矩阵分解在下面这两点上是有缺陷的，需要采用其他的方式来弥补或者避免。

(1) 存在冷启动问题
当某个用户的用户行为很少时，我们基本无法利用矩阵分解获得该用户比较精确的特征向量表示，因此无法为该用户生成推荐结果。这时可以借助内容推荐算法来为该用户生成推荐。对于新入库的标的物也一样，可以采用人工编排的方式将标的物做适当的曝光获得更多用户对标的物的操作行为，从而方便算法将该标的物推荐出去。参考文献9中提供了一种解决矩阵分解冷启动问题的有效算法lightFM，通过将metadata信息整合到矩阵分解中，可以有效解决冷启动问题，对于操作行为不多的用户以及新上线不久还未收集到更多用户行为的标的物都有比较好的推荐效果。该论文的lightFM算法在github上有相应的python代码实现(参见https://github.com/lyst/lightfm)，可以作为很好的学习材料。

(2) 可解释性不强
矩阵分解算法通过矩阵分解获得用户和标的物的(嵌入)特征表示，这些特征是隐式的，无法用现实中的显示特征进行解释，因此利用矩阵分解算法做出的推荐，我们无法对推荐结果进行解释，只能通过离线或者在线评估来评价算法的效果。不像user-based和item-based协同过滤算法基于非常朴素的”物以类聚、人以群分“的思想，可以非常容易做解释。

因子分解机

基本思想

因子分解机(Factorization Machine，简称FM，中文简称为分解机)，该算法的核心思路来源于矩阵分解算法，矩阵分解算法可以看成是分解机的特例。

与传统的简单线性模型不同的是，因子分解机考虑了特征间的交叉，对所有特征变量交互进行建模（类似于SVM中的核函数），因此在推荐系统和计算广告领域关注的点击率CTR（click-through rate）和转化率CVR（conversion rate）两项指标上有着良好的表现。此外，FM模型还具备可以用线性时间来计算，可以整合多种信息，以及能够与许多其他模型相融合等优点。

我们常用的简单模型有线性回归模型及logistic回归模型(LR)(见下面两个公式)，它们都是简单的线性模型，原理简单，易于理解，并且非常容易训练，对于一般的分类及预测问题，可以提供简单的解决方案。但是，特征之间是彼此独立的，无法拟合特征之间的非线性关系，而现实生活中往往特征之间不是独立的而是存在一定的内在联系，以新闻推荐为例，一般男性用户看军事新闻多，而女性用户喜欢情感类新闻，那么可以看出性别与新闻的类别有一定的关联性，如果能找出这类相关的特征，是非常有意义的，可以显著提升模型预测的准确度。

LR模型是CTR预估领域早期最成功的模型，也大量用于推荐算法排序阶段，大多工业推荐排序系统通过整合人工非线性特征，最终采用这种“线性模型+人工特征组合引入非线性”的模式来训练LR模型。因为LR模型具有简单、方便易用、解释强、易于分布式实现等诸多好处，所以目前工业上仍然有不少算法系统采取这种模式。但是，LR模型最大的缺陷就是人工特征工程，耗时费力，浪费大量人力资源来筛选组合非线性特征，那么能否将特征组合的能力体现在模型层面呢？也即，是否有一种模型可以自动化地组合筛选交叉特征呢？答案是肯定的。其实想达到这一点并不难，如上图在线性模型的计算公式里加入二阶特征组合即可，任意两个特征进行两两组合，可以将这些组合出的特征看作一个新特征，加入线性模型中。而组合特征的权重和一阶特征权重一样，在训练阶段学习获得。其实这种二阶特征组合的使用方式，和多项式核SVM是等价的。借助SVM中核函数的思路，我们可以在线性模型中整合二阶交叉特征，得到如下的模型。

那么我们有办法解决该问题吗？其实是有的，我们可以借助矩阵分解的思路，对二阶交叉特征的系数进行调整，让系数不在是独立无关的，从而减少模型独立系数的数量，解决由于数据稀疏导致无法训练出参数的问题，具体是将上面的模型修改为

由于在稀疏情况下，没有足够的训练数据来支撑模型训练，一般选择较小的k，虽然模型表达空间变小了，但是在稀疏情况下可以达到较好的效果，并且有很好的拓展性。
计算复杂度

由于分解机模型可以在线性时间下计算出，对于我们做预测是非常有价值的，特别是对互联网产品有海量用户的情况。拿推荐来说，我们每天需要为每个用户计算推荐(这是离线推荐，实时推荐计算量会更大)，线性时间复杂度可以让整个计算过程更加高效，可以在更短的时间完成计算，节省服务器资源。

应用

分解机可以作为一般的预测模型，用于回归和分类，特别是用在推荐系统和广告点击率预估等商业场景。分解机在推荐系统上的应用，可以采用回归和预测两类方法。当我们预测用户对标的物的评分时，就是回归问题，当我们预测用户对标的物是否点击时，可以看成是一个二分类问题，这时可以通过增加一个logit变换，转化为预测用户点击的概率问题。

怎么构建FM需要的特征，有哪些信息可以作为模型的输入。构建FM模型的特征主要分为如下4大类，我们来分别介绍。

1.用户与标的物的交互行为信息
包括用户的点击、播放、收藏、搜索、点赞等各种(隐式)行为。这些行为可以通过平展化的方式整合为特征。比如有n个用户，m个标的物。那么用户对某个标的物的行为平展化为n+m维的特征子向量，其中用户和标的物所在的列非零，其他为零，如下图。

上图是用户行为的隐式操作转化为特征子向量，特征用0或者1表示，有隐式操作则为1，否则为0。也可以采用将用户的每一种操作作为一个维度，每个维度的值代表用户是否操作过或者对应的操作得分(比如用户播放时长占视频总时长的比例作为得分)，如下图。

2.用户相关信息
用户相关的信息有很多，包括人口统计学信息，如年龄、性别、职业、收入、地域、受教育程度等等。另外还可以包括用户行为信息，用户是否是会员、什么时候注册过、最后一次登录时间、最后一次付费时间等。这些信息都可以作为某一个维度的特征灌入到FM模型中。

3.标的物相关信息
标的物的metadata信息都可以作为FM的特征，拿电影推荐来说，电影的评分、年代、标签、演职员、是否获奖、是否高清、地区、语言、是否是付费节目等都可以作为特征。其中评分、年代是数值特征，标签、演职员是类别特征，可以采用n-hot编码(每个电影有多个标签，对应标签上的值为1，所以这里叫做n-hot编码，而不是one-hot)。另外该节目的用户行为也可以作为特征，比如节目播放次数、节目平均播放完成度等。

4.上下文信息
用户在操作标的物时，是包含上下文信息的，这类上下文
主要有时间、地点、上一步操作、所在路径、甚至是天气、心情等。时间可以是操作时间、是否是节日、是否是工作日、特殊事件(如双十一)、操作系统、版本等。地域对于LBS类应用是非常重要的。对于像购物等具备漏斗行为转化的产品或业务，用户的上一步操作及所在路径对训练模型非常关键。整合了上述4大类信息，我们可以构建如下的训练集，利用FM模型来训练，求得参数，最终获得训练好的模型，用于线上预测。

优势

分解机的优势

FM之所以在学术界和工业界受到追捧，得益于它各种优点，这些优点主要体现在如下几个方面。

(1) 可以整合交叉特征，效果不错
在真实业务场景中，往往特征之间的交叉对模型预测是非常有帮助的，而分解机可以自动整合二阶(高阶)交叉特征，免去了人工特征工程(如logistic回归需要大量的人工特征工程)的工作，从而(相比矩阵分解及logistic回归等模型)可以达到更好的训练效果。

(2) 线性时间复杂度
FM通过将预测函数做数学变换，将二阶交叉特征的计算从二阶多项式的复杂度降低到线性复杂度，方便模型预测和通过SGD等迭代方法估计参数， 从而让FM在工业界的大规模数据场景下的应用(推荐系统、CTR预估等)变得可行。

(3) 可以应对稀疏数据情况
FM通过分解二阶交叉特征的系数到低维空间，避免了交叉特征的系数独立的情况，减少了参数空间，并且由于不同交叉项之间的系数是有关联的，在高度稀疏的情况下，也可以容易估计模型系数，模型泛化能力强。

(4) 模型相对简单，易于工程实现
FM模型原理非常简单，思想也很朴素，并且预测过程可以降低到线性时间复杂度，可以采用SGD等常用算法来进行训练，在工程实现上是相对容易的，有很多开源的工具都有FM的实现，我们可以直接拿来用。正因为工程实现简单，才在工业界得到大规模的推广和应用。