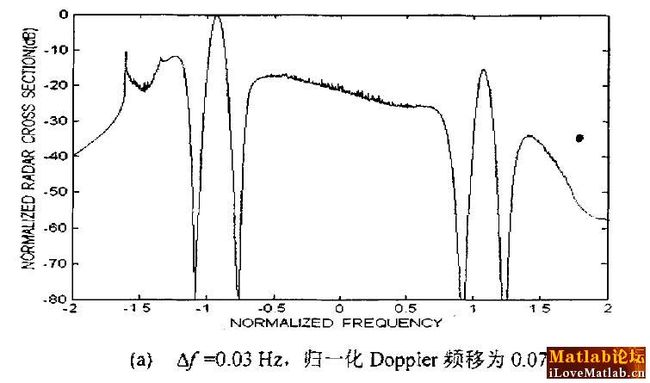
matlab 海谱,Matlab高频雷达海洋回波谱的模拟仿真
海杂波模拟仿真图.JPG (42.09 KB, 下载次数: 428)
2009-3-29 12:34 上传
不知道为何和结果不一样啊!请教高手帮忙
Q1:何为对冲击进行高斯平滑?(对应于图中-1,1位置原本是两个冲击,平滑后变成有一定宽度的尖峰?)
Q2: 两个尖峰周围二阶谱的部分编程如何实现的啊?我下面的程序有什么不妥的么?%------------------------------一、二阶海杂波谱仿真图------------------------%
%-------------------线性调频连续波发射信号仿真------------------------------%
clc;
clear all;
close all;
%---------------------初始参数设置-----------------------------------------%
T = 0.25; % 脉冲宽度(即脉冲重复周期)
TT =64; % 相干积累时间
N = TT/T; % 相干积累时间内的脉冲数
% Fs = B*2; % 采样频率
saNum = 5; % 每个周期的采样点数
Ts = T/saNum; % 采样间隔
sig_ran = 60; % 目标所在的距离单元
Fs = 10e2;
%--------------------------------发射信号仿真------------------------------%
tt = Ts:Ts:T;
t = 0:1/(Fs):TT;
%--------------------------------海杂波信号仿真-----------------------------%
%------------------------------------第一种--------------------------------%
% 一阶海杂波
f0 = 18e6; % 雷达载频
g = 9.8; % 重力加速度
c = 3e8;
lambda = c/f0; % 电磁波波长
alfa = 8.1e-3;
beita = 0.74;
U = 25; % 待变参数,海面上19.5m处的风速
kc = g/U^2 ; %截止波束
theta = 180; % 雷达波束方向到海浪波列前进方向的转角
fi = 0; % 雷达波束方向的方位角
% theta+fi %表示海浪波列前进方向的方位角
fw = 90 ; %海面风向的方位角
k0 = 2*pi/lambda;
fd1 = 0.1012 * (f0/1e6)^0.5; % 一阶Bragg峰的多普勒频率,存在洋流时偏移
fd2 = -fd1;
S1 = 0.005*(-2*k0)^-4*exp(-0.74*(kc/(2*k0))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
S2 = 0.005*(-2*k0)^-4*exp(-0.74*(kc/(2*k0))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
G1_1 = 4/(3*pi)*(cos((180-fw)*pi/180/2))^4;
G2_1 = 4/(3*pi)*(cos((0-fw)*pi/180/2))^4;
Bragg1_1 = 2^6*k0^4*pi*S1*G1_1*exp(2*pi*1i*fd1.*t).*exp(-(t).^2./((2^2)*0.4))./((2*pi)^0.5*0.4); % 正轴一阶Bragg峰
Bragg1_2 = 2^6*k0^4*pi*S2*G2_1*exp(2*pi*1i*fd2.*t).*exp(-(t).^2./((2^2)*0.4))./((2*pi)^0.5*0.4); % 负轴一阶Bragg峰
% Noise = 1.2358e-004*randn(1,length(t));%2^9也行
freq = linspace(-Fs/2,Fs/2,length(t));
B_1 = fftshift(abs(fft(Bragg1_1+Bragg1_2)));
% B_11 = B_1/max(B_1);
% B_11 = 20*log10(B_11);
% figure(1);
% plot(freq,B_11); %一阶bragg峰
% xlim([-2 2]);
% 二阶海杂波
f4 = linspace(-1.1*fd1,-2*fd1,20);
f3 = linspace(-0.9*fd1,-0.1*fd1,80);
f1 = linspace(0.1*fd1,0.9*fd1,80);
f2 = linspace(1.1*fd1,2*fd1,20);
delta_k = k0/40;
delta = 0.011 - i*(0.0121);
for n = 1:79
k_n = n*delta_k;
for i = 1:length(f1)
%m=-1,m^=1
% if k_n-2*k0< k_p < k_n+2*k0
theta = linspace(0,180,181);
k_p = (2*pi*f1(i)+(g*k_n)^0.5)^2/g;
% theta_1 = acos((k_p^2-k_n^2-4*k0^2)/4*k_n*k0);
theta_2 = asin(k_n*sin(k_n*sin(theta.*pi/180)./k_p))-pi;
kafang1 = -i*0.5*(k_n+k_p-k_n*k_p*((2*pi*f1(i))^2+(2*pi*fd1)^2)/(k_n*k_p)^0.5/((2*pi*f1(i))^2-(2*pi*fd1)^2));
kafang2 = 0.5*(k_n*k0*-cos(theta.*pi/180).*(k_p*k0*-cos(theta_2.*pi/180))./k0^3/delta);
kafang = (abs(kafang1+kafang2)).^2*2^6*k0^4*pi*n*(delta_k^2);
S1 = 0.005*(-k_n).^-4*exp(-0.74*(kc/(-k_n))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
S2 = 0.005*(k_p).^-4*exp(-0.74*(kc/(k_p))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
G1 = 4/(3*pi)*(cos((theta-fw).*pi/180/2)).^4;
G2 = 4/(3*pi)*(cos((theta_2-fw).*pi/180/2)).^4;
X(i) = trapz(kafang.*G1.*G2.*S1.*S2,theta.*pi/180);
theta = linspace(-180,0,181);
k_p = (2*pi*f1(i)+(g*k_n)^0.5)^2/g;
% theta_1 = acos((k_p^2-k_n^2-4*k0^2)/4*k_n*k0);
theta_2 = asin(k_n*sin(k_n*sin(theta.*pi/180)./k_p))+pi;
kafang1 = -i*0.5*(k_n+k_p-k_n*k_p*((2*pi*f1(i))^2+(2*pi*fd1)^2)/(k_n*k_p)^0.5/((2*pi*f1(i))^2-(2*pi*fd1)^2));
kafang2 = 0.5*(k_n*k0*-cos(theta.*pi/180).*(k_p*k0*-cos(theta_2.*pi/180))./k0^3/delta);
kafang = (abs(kafang1+kafang2)).^2*2^6*k0^4*pi*n*(delta_k^2);
S1 = 0.005*(-k_n).^-4*exp(-0.74*(kc/(-k_n))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
S2 = 0.005*(k_p).^-4*exp(-0.74*(kc/(k_p))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
G1 = 4/(3*pi)*(cos((theta-fw).*pi/180/2)).^4;
G2 = 4/(3*pi)*(cos((theta_2-fw).*pi/180/2)).^4;
Y(i) = trapz(kafang.*G1.*G2.*S1.*S2,theta.*pi/180);
%m=1,m^=-1
theta = linspace(0,180,181);
k_p = (2*pi*f1(i)-(g*k_n)^0.5)^2/g;
% theta_1 = acos((k_p^2-k_n^2-4*k0^2)/4*k_n*k0);
theta_2 = asin(k_n*sin(k_n*sin(theta.*pi/180)./k_p))-pi;
kafang1 = -i*0.5*(k_n+k_p-k_n*k_p*((2*pi*f1(i))^2+(2*pi*fd1)^2)/(k_n*k_p)^0.5/((2*pi*f1(i))^2-(2*pi*fd1)^2));
kafang2 = 0.5*(k_n*k0*-cos(theta.*pi/180).*(k_p*k0*-cos(theta_2.*pi/180))./k0^3/delta);
kafang = (abs(kafang1+kafang2)).^2*2^6*k0^4*pi*n*(delta_k^2);
S1 = 0.005*(k_n).^-4*exp(-0.74*(kc/(k_n))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
S2 = 0.005*(-k_p).^-4*exp(-0.74*(kc/(-k_p))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
G1 = 4/(3*pi)*(cos((theta-fw).*pi/180/2)).^4;
G2 = 4/(3*pi)*(cos((theta_2-fw).*pi/180/2)).^4;
A(i) = trapz(kafang.*G1.*G2.*S1.*S2,theta.*pi/180);
theta = linspace(-180,0,181);
k_p = (2*pi*f1(i)-(g*k_n)^0.5)^2/g;
% theta_1 = acos((k_p^2-k_n^2-4*k0^2)/4*k_n*k0);
theta_2 = asin(k_n*sin(k_n*sin(theta.*pi/180)./k_p))+pi;
kafang1 = -i*0.5*(k_n+k_p-k_n*k_p*((2*pi*f1(i))^2+(2*pi*fd1)^2)/(k_n*k_p)^0.5/((2*pi*f1(i))^2-(2*pi*fd1)^2));
kafang2 = 0.5*(k_n*k0*-cos(theta.*pi/180).*(k_p*k0*-cos(theta_2.*pi/180))./k0^3/delta);
kafang = (abs(kafang1+kafang2)).^2*2^6*k0^4*pi*n*(delta_k^2);
S1 = 0.005*(k_n).^-4*exp(-0.74*(kc/(k_n))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
S2 = 0.005*(-k_p).^-4*exp(-0.74*(kc/(-k_p))^2);% 两个Bragg峰的幅度不同(随海面风向的方向角)
G1 = 4/(3*pi)*(cos((theta-fw).*pi/180/2)).^4;
G2 = 4/(3*pi)*(cos((theta_2-fw).*pi/180/2)).^4;
B(i) = trapz(kafang.*G1.*G2.*S1.*S2,theta.*pi/180);
Bragg(i,:) = (X(i)+Y(i)+A(i)+B(i))*exp(2*pi*1i*f1(i)*t);
end
Bragg1(n,:) = sum(Bragg,1);
% end
end
BB2 = sum(Bragg1,1)./10;
B_2 = fftshift(abs(fft(BB2)));
% BB2 = B_2/max(B_2);
% BB2 = 20*log10(BB2);
% figure(3)
% plot(freq,B_2);
% xlim([-2 2]);
for n = 1:79
k_n = n*delta_k;
for i = 1:length(f3)
%m=1,m^=-1
% if k_n-2*k0< k_p < k_n+2*k0
theta = linspace(0,180,181);
k_p = (2*pi*f1(i)-(g*k_n)^0.5)^2/g;
% theta_1 = acos((k_p^2-k_n^2-4*k0^2)/4*k_n*k0);
theta_2 = asin(k_n*sin(k_n*sin(theta.*pi/180)./k_p))-pi;
kafang1 = -i*0.5*(k_n+k_p-k_n*k_p*((2*pi*f1(i))^2+(2*pi*fd1)^2)/(k_n*k_p)^0.5/((2*pi*f1(i))^2-(2*pi*fd1)^2));
kafang2 = 0.5*(k_n*k0*-cos(theta.*pi/180).*(k_p*k0*-cos(theta_2.*pi/180))./k0^3/delta);
kafang = (abs(kafang1+kafang2)).^2*2^6*k0^4*pi*n*(delta_k^2);
S1 = 0.005*(k_n).^-4*exp(-0.74*(kc/(k_n))^2);% )
S2 = 0.005*(-k_p).^-4*exp(-0.74*(kc/(-k_p))^2);%)
G1 = 4/(3*pi)*(cos((theta-fw).*pi/180/2)).^4;
G2 = 4/(3*pi)*(cos((theta_2-fw).*pi/180/2)).^4;
X(i) = trapz(kafang.*G1.*G2.*S1.*S2,theta.*pi/180);
BBB = B_1+B_2 +B_3 ;
BBB = BBB/max(BBB);
BBB = 20*log10(BBB);
plot(freq,BBB);
xlabel('多普勒频率(Hz)');ylabel('归一化回波功率(dB)');
xlim([-2 2]);ylim([-80 0])
[本帖最后由 mengze 于 2009-3-29 15:30 编辑]