机器学习-白板推导系列(三)-线性回归
3. 线性回归
-
本章内容:
1、最小二乘法(矩阵表达与几何意义)
2、概率角度: 最 小 二 乘 法 ⇔ n o i s e 为 G a u s s i a n 的 M L E ( 最 大 似 然 估 计 ) 最小二乘法\Leftrightarrow noise为Gaussian 的 MLE(最大似然估计) 最小二乘法⇔noise为Gaussian的MLE(最大似然估计)
3、正则化
{ L 1 → L a s s o L 2 → R i d g e ( 岭 回 归 ) \begin{cases} L1 \rightarrow Lasso\\ L2 \rightarrow Ridge(岭回归)\\ \end{cases} {L1→LassoL2→Ridge(岭回归) -
数据如下:
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } , x i ∈ R p , y i ∈ R , i = 1 , 2 , ⋯ , N D=\left \{(x_{1},y_{1}),(x_{2},y_{2}),\cdots ,(x_{N},y_{N})\right \}, x_{i}\in \mathbb{R}^{p},y_{i}\in \mathbb{R},i=1,2,\cdots ,N D={(x1,y1),(x2,y2),⋯,(xN,yN)},xi∈Rp,yi∈R,i=1,2,⋯,N
X = ( x 1 , x 1 , ⋯ , x N ) T = ( x 1 T x 2 T ⋮ x N T ) = ( x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x N 1 x N 2 ⋯ x N p ) N × p X=(x_{1},x_{1},\cdots ,x_{N})^{T}=\begin{pmatrix} x_{1}^{T}\\ x_{2}^{T}\\ \vdots \\ x_{N}^{T} \end{pmatrix}=\begin{pmatrix} x_{11} & x_{12} & \cdots &x_{1p} \\ x_{21} & x_{22}& \cdots &x_{2p} \\ \vdots & \vdots & \ddots &\vdots \\ x_{N1}& x_{N2} & \cdots & x_{Np} \end{pmatrix}_{N \times p} X=(x1,x1,⋯,xN)T=⎝⎜⎜⎜⎛x1Tx2T⋮xNT⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11x21⋮xN1x12x22⋮xN2⋯⋯⋱⋯x1px2p⋮xNp⎠⎟⎟⎟⎞N×p
Y = ( y 1 y 2 ⋮ y N ) N × 1 Y=\begin{pmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{N} \end{pmatrix}_{N \times 1} Y=⎝⎜⎜⎜⎛y1y2⋮yN⎠⎟⎟⎟⎞N×1这些数据符合下图关系(以一维数据为例),这里的函数 f ( w ) = W T x i + b f(w)=W^Tx_i+b f(w)=WTxi+b,此处在 x i x_i xi中增加一个 x i 0 = 1 x_{i0}=1 xi0=1 ,在 W W W 中增加一个 w 0 = b w_0=b w0=b ,即可用 W T x i W^Tx_i WTxi表示。
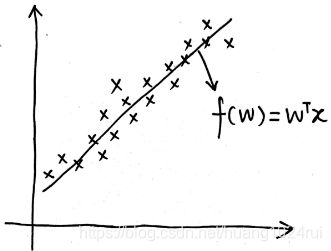
1. 最小二乘法及其几何意义
1.1 最小二乘法
- 定义损失函数(Loss Function)
采用二范数定义的平方误差来定义损失函数(Loss Function):
L ( W ) = ∑ i = 1 N ∣ ∣ W T x i − y i ∣ ∣ 2 2 L(W)=\sum\limits_{i=1}^N||W^Tx_i-y_i||^2_2 L(W)=i=1∑N∣∣WTxi−yi∣∣22- 此式为均方差,若 L L L越小,则回归结果与真实结果越接近;
- 此处 W W W是一个 p × 1 p\times 1 p×1的向量,表示 x i x_i xi的系数;
- 在 x i x_i xi中增加一个 x i 0 = 1 x_{i0}=1 xi0=1 ,在 W W W 中增加一个 w 0 = b w_0=b w0=b ,即可用 W T x i W^Tx_i WTxi表示。
- 求解 L ( W ) L(W) L(W)
L ( W ) = ∑ i = 1 N ( W T x i − y i ) 2 = ( W T x 1 − y 1 W T x 2 − y 2 ⋯ W T x N − y N ) ( ( W T x 1 − y 1 ) T ( W T x 2 − y 2 ) T ⋮ ( W T x N − y N ) T ) = [ W T ( x 1 x 2 ⋯ x N ) − ( y 1 y 2 ⋯ y N ) ] ( x 1 T W − y 1 T x 2 T W − y 2 T ⋮ x N T W − y N T ) = ( W T X T − Y T ) ( X W − Y ) = W T X T X W − W T X T Y − Y T X W + Y T Y = W T X T X W − 2 W T X T Y + Y T Y \begin{array}{l} L(W)&=\displaystyle\sum^{N}_{i=1}(W^Tx_i-y_i)^2\\ &= \begin{pmatrix} W^Tx_1-y_1 & W^Tx_2-y_2&\cdots&W^Tx_N-y_N \end{pmatrix} \begin{pmatrix} (W^Tx_1-y_1)^T\\(W^Tx_2-y_2)^T\\\vdots\\(W^Tx_N-y_N)^T \end{pmatrix}\\ &=[W^T\begin{pmatrix} x_1&x_2&\cdots&x_N \end{pmatrix} -\begin{pmatrix} y_1&y_2&\cdots&y_N \end{pmatrix}] \begin{pmatrix} x_1^TW-y_1^T\\x_2^TW-y_2^T\\\vdots\\x_N^TW-y_N^T \end{pmatrix}\\ &=(W^TX^T - Y^T)(XW-Y)\\ &=W^TX^TXW-W^TX^TY-Y^TXW+Y^TY\\ &=W^TX^TXW-2W^TX^TY+Y^TY\end{array} L(W)=i=1∑N(WTxi−yi)2=(WTx1−y1WTx2−y2⋯WTxN−yN)⎝⎜⎜⎜⎛(WTx1−y1)T(WTx2−y2)T⋮(WTxN−yN)T⎠⎟⎟⎟⎞=[WT(x1x2⋯xN)−(y1y2⋯yN)]⎝⎜⎜⎜⎛x1TW−y1Tx2TW−y2T⋮xNTW−yNT⎠⎟⎟⎟⎞=(WTXT−YT)(XW−Y)=WTXTXW−WTXTY−YTXW+YTY=WTXTXW−2WTXTY+YTYW T X T Y = ( Y T X W ) T W^TX^TY=(Y^TXW)^T WTXTY=(YTXW)T是因为:
W T X T Y ∈ R 1 W^TX^TY\in \mathbb{R}^{1} WTXTY∈R1,所以: W T X T Y = Y T X W W^TX^TY=Y^TXW WTXTY=YTXW - 最优 W W W使得 L L L 最小:
最优 W W W使得 L L L 最小,即对下式进行处理:
W ^ = a r g m i n W L ( W ) \hat W=\underset {W}{argmin}L(W) W^=WargminL(W)
∂ L ( W ) ∂ W = 2 X T X W − 2 X T Y = 0 {\partial L(W)\over\partial W}=2X^TXW-2X^TY=0 ∂W∂L(W)=2XTXW−2XTY=0
则: W = ( X T X ) − 1 X T Y = X + Y \color{red}W=(X^TX)^{-1}X^TY=X^+Y W=(XTX)−1XTY=X+Y- 其中: ∂ ( W T X T X W ) ∂ W = X T X W + ( X T X ) T W = 2 X T X W {\partial (W^TX^TXW)\over\partial W}=X^TXW+(X^TX)^TW=2X^TXW ∂W∂(WTXTXW)=XTXW+(XTX)TW=2XTXW。
- ( X T X ) − 1 X T \color{blue}(X^TX)^{-1}X^T (XTX)−1XT为伪逆,记作: X + \color{red}X^+ X+。
- 此处 ( X T X ) − 1 X T \color{blue}(X^TX)^{-1}X^T (XTX)−1XT 为 X X X 的 左 逆 X l e f t − 1 \color{blue}左逆X_{left}^{-1} 左逆Xleft−1。( X l e f t − 1 ⋅ X = ( X T X ) − 1 ( X T X ) = I X_{left}^{-1}\cdot X=(X^TX)^{-1}(X^TX)=I Xleft−1⋅X=(XTX)−1(XTX)=I)
- 对于 行 满 秩 或 者 列 满 秩 \color{red}行满秩或者列满秩 行满秩或者列满秩的 X X X可以直接求解,但是对于 非 满 秩 \color{red}非满秩 非满秩的样本集合,需要使用 奇 异 值 分 解 ( S V D ) \color{red}奇异值分解(SVD) 奇异值分解(SVD)的方法,对 X X X求奇异值分解,得到
X = U Σ V T X=U\Sigma V^T X=UΣVT
于是: X + = V Σ − 1 U T X^+=V\Sigma^{-1}U^T X+=VΣ−1UT
1.2 最小二乘法的几何意义
1.2.1 从每个数据点的误差角度

使用最小二乘法可以看做损失函数是每个样本的误差的总和,每个样本的误差即是 y i y_{i} yi与 w T x i w^{T}x_{i} wTxi的差,因此将所有点的误差求和 ∑ i = 1 N ∥ W T x i − y i ∥ 2 \displaystyle\sum^{N}_{i=1}{\Vert W^Tx_i-y_i\Vert}^2 i=1∑N∥WTxi−yi∥2,使得其最小,便可求得最优的回归函数。
1.2.2 从投影角度
从投影角度来看最小二乘法推荐去看MIT 线性代数的课程,其中专门有一节讲最小二乘法,可以看看我的博客:第十六讲 投影矩阵(Ax=b)和最小二乘法
-
实质
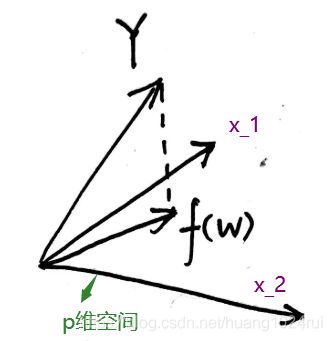
从投影角度的实质是: Y Y Y在 X X X的列空间上的投影。
X N × p W p × 1 = ( x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x N 1 x N 2 ⋯ x N P ) ( w 1 w 2 ⋮ w p ) = ( x 11 w 1 + x 12 w 2 + ⋯ + x 1 p w p x 21 w 1 + x 22 w 2 + ⋯ + x 2 p w p ⋮ x N 1 w 1 + x N 2 w 2 + ⋯ + x N p w p ) = ( w 1 ( x 11 x 21 ⋮ x N 1 ) + w 2 ( x 12 x 22 ⋮ x N 2 ) + ⋯ + w p ( x 1 p x 2 p ⋮ x N p ) ) \begin{array}{l} X_{N\times p}W_{p \times 1}&= \begin{pmatrix} x_{11}&x_{12} & \cdots& x_{1p}\\ x_{21}&x_{22}&\cdots&x_{2p}\\ \vdots&\vdots&\ddots&\vdots\\ x_{N1}&x_{N2}&\cdots &x_{NP} \end{pmatrix} \begin{pmatrix} w_1\\w_2\\\vdots\\w_p \end{pmatrix}\\ &=\begin{pmatrix} x_{11}w_1+x_{12}w_2+\cdots+x_{1p}w_p\\ x_{21}w_1+x_{22}w_2+\cdots+x_{2p}w_p\\ \vdots\\ x_{N1}w_1+x_{N2}w_2+\cdots+x_{Np}w_p \end{pmatrix}\\ &=\begin{pmatrix} w_1\begin{pmatrix}x_{11}\\x_{21}\\\vdots\\x_{N1}\end{pmatrix} +w_2\begin{pmatrix}x_{12}\\x_{22}\\\vdots\\x_{N2}\end{pmatrix} +\cdots+ w_p\begin{pmatrix}x_{1p}\\x_{2p}\\\vdots\\x_{Np}\end{pmatrix} \end{pmatrix} \end{array} XN×pWp×1=⎝⎜⎜⎜⎛x11x21⋮xN1x12x22⋮xN2⋯⋯⋱⋯x1px2p⋮xNP⎠⎟⎟⎟⎞⎝⎜⎜⎜⎛w1w2⋮wp⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11w1+x12w2+⋯+x1pwpx21w1+x22w2+⋯+x2pwp⋮xN1w1+xN2w2+⋯+xNpwp⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛w1⎝⎜⎜⎜⎛x11x21⋮xN1⎠⎟⎟⎟⎞+w2⎝⎜⎜⎜⎛x12x22⋮xN2⎠⎟⎟⎟⎞+⋯+wp⎝⎜⎜⎜⎛x1px2p⋮xNp⎠⎟⎟⎟⎞⎠⎟⎟⎟⎞一组向量的生成子空间(span)是原始向量线性组合后所能抵达的点的集合。确定方程 A x = b Ax=b Ax=b是否有解,相当于确定向量 b b b是否在 A A A列向量的生成子空间中。这个特殊的生成子空间被称为 A A A的 列 空 间 ( c o l u m n s p a c e ) \color{red}列空间(column space) 列空间(columnspace)或者 A A A的 值 域 ( r a n g e ) \color{red}值域(range) 值域(range)。
假设我们的试验样本张成一个 p p p 维空间(满秩的情况): X = S p a n ( x 1 , ⋯ , x N ) , x i ∈ R p X=Span(x_1,\cdots,x_N),\\x_{i}\in \mathbb{R}^{p} X=Span(x1,⋯,xN),xi∈Rp,而模型可以写成 f ( w ) = X W f(w)=XW f(w)=XW,也就是 x 1 , ⋯ , x N x_1,\cdots,x_N x1,⋯,xN 的某种组合,而最小二乘法就是说希望 Y Y Y 和这个模型距离越小越好,于是它们的差应该与这个张成的空间垂直:
X T ⋅ ( Y − X W ) = 0 ⟶ W = ( X T X ) − 1 X T Y X^T\cdot(Y-XW)=0\longrightarrow W=(X^TX)^{-1}X^TY XT⋅(Y−XW)=0⟶W=(XTX)−1XTY如下图所示, 虚 线 \color{red}虚线 虚线部分为 Y − X W Y-XW Y−XW,其 垂 直 \color{red}垂直 垂直于 X X X列空间(即与 X X X的每一个列向量都垂直),因此: X T ( Y − X W ) = 0 X^T(Y-XW)=0 XT(Y−XW)=0,所以:
W = ( X T X ) − 1 X T Y W=(X^TX)^{-1}X^TY W=(XTX)−1XTY
1.2.3 总结:
- 第一种角度是把误差分散在了每一个数据点上
- 第二种角度是把误差分散在了 X X X的每一个列向量上, p p p个维度上面。
不同的角度得到了同样的结果
横看成岭侧成峰,体现了数学的美!
2. 最小二乘法+概率视角-高斯噪声-MLE
2.1 线性回归结论
- 数据:
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } , x i ∈ R p , y i ∈ R , i = 1 , 2 , ⋯ , N D=\left \{(x_{1},y_{1}),(x_{2},y_{2}),\cdots ,(x_{N},y_{N})\right \}, x_{i}\in \mathbb{R}^{p},y_{i}\in \mathbb{R},i=1,2,\cdots ,N D={(x1,y1),(x2,y2),⋯,(xN,yN)},xi∈Rp,yi∈R,i=1,2,⋯,N
X = ( x 1 , x 1 , ⋯ , x N ) T = ( x 1 T x 2 T ⋮ x N T ) = ( x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x N 1 x N 2 ⋯ x N p ) N × p Y = ( y 1 y 2 ⋮ y N ) N × 1 X=(x_{1},x_{1},\cdots ,x_{N})^{T}=\begin{pmatrix} x_{1}^{T}\\ x_{2}^{T}\\ \vdots \\ x_{N}^{T} \end{pmatrix}=\begin{pmatrix} x_{11} & x_{12} & \cdots &x_{1p} \\ x_{21} & x_{22}& \cdots &x_{2p} \\ \vdots & \vdots & \ddots &\vdots \\ x_{N1}& x_{N2} & \cdots & x_{Np} \end{pmatrix}_{N \times p}\;Y=\begin{pmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{N} \end{pmatrix}_{N \times 1} X=(x1,x1,⋯,xN)T=⎝⎜⎜⎜⎛x1Tx2T⋮xNT⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11x21⋮xN1x12x22⋮xN2⋯⋯⋱⋯x1px2p⋮xNp⎠⎟⎟⎟⎞N×pY=⎝⎜⎜⎜⎛y1y2⋮yN⎠⎟⎟⎟⎞N×1 - 最小二乘估计
求解: L ( W ) = ∑ i = 1 N ∥ W T x i − y i ∥ 2 L(W)=\displaystyle\sum^{N}_{i=1}{\Vert W^Tx_i-y_i\Vert}^2 L(W)=i=1∑N∥WTxi−yi∥2
得到: W ^ = a r g m i n W L ( W ) ; W ^ = ( X T X ) − 1 X T Y \hat W=arg\underset {W}{min}L(W);\;\hat W=(X^TX)^{-1}X^TY W^=argWminL(W);W^=(XTX)−1XTY
2.2 概率角度-高斯噪声
现实中不可能出现 Y Y Y在 X X X的张成空间中,因为数据都带有一定的噪声。
- 假设噪声 ϵ ∼ N ( 0 , σ 2 ) \epsilon\sim N(0,\sigma^2) ϵ∼N(0,σ2),因为 f ( W ) = y = W T X , y = f ( W ) + ϵ f(W)=y=W^TX,\;y = f(W)+\epsilon f(W)=y=WTX,y=f(W)+ϵ,因此 y = W T X + ϵ y=W^TX+\epsilon y=WTX+ϵ
此处把 W T X W^TX WTX看成 常 数 \color{red}常数 常数,因为当 W W W固定后, W T X W^TX WTX是固定值。
- 因此 y ∣ X , W ∼ N ( w T x , σ 2 ) \color{red}y|X,W\sim N(w^{T}x,\sigma ^{2}) y∣X,W∼N(wTx,σ2),即 P ( y ∣ X , W ) = 1 2 π σ e x p { − ( y − W T X ) 2 2 σ 2 } P(y|X,W)=\frac{1}{\sqrt{2\pi }\sigma }exp\left \{-\frac{(y-W^{T}X)^{2}}{2\sigma ^{2}}\right \} P(y∣X,W)=2πσ1exp{−2σ2(y−WTX)2}可以使用MLE(最大似然估计)法来进行求解:
L ( W ) = log p ( y ∣ X , W ) = log ∏ i = 1 N p ( y i ∣ x i , W ) = ∑ i = 1 N log p ( y i ∣ x i , W ) = ∑ i = 1 N log ( 1 2 π σ exp ( − ( y i − W T x i ) 2 2 σ 2 ) ) = ∑ i = 1 N log 1 2 π σ − ( y i − W T x i ) 2 2 σ 2 \begin{array}{l}L(W)&=\log{p(y|X,W)}\\ &=\log\displaystyle\prod^N_{i=1}{p(y_i|x_i,W)}\\ &=\displaystyle\sum^N_{i=1}{\log p(y_i|x_i,W)}\\ &=\displaystyle\sum^N_{i=1}{\log ({1\over \sqrt{2\pi}\sigma}\exp(-{(y_i-W^Tx_i)^2\over 2\sigma^2})})\\ &=\displaystyle\sum^N_{i=1}\log{{1\over \sqrt{2\pi}\sigma}-{(y_i-W^Tx_i)^2\over 2\sigma^2}} \end{array} L(W)=logp(y∣X,W)=logi=1∏Np(yi∣xi,W)=i=1∑Nlogp(yi∣xi,W)=i=1∑Nlog(2πσ1exp(−2σ2(yi−WTxi)2))=i=1∑Nlog2πσ1−2σ2(yi−WTxi)2 - 求解 L ( W ) L(W) L(W)
W ^ = a r g m a x W L ( W ) = a r g m a x W ∑ i = 1 N log 1 2 π σ − ( y i − W T x i ) 2 2 σ 2 ⇔ a r g m a x W ∑ i = 1 N − ( y i − W T x i ) 2 2 σ 2 ⇔ a r g m i n W ∑ i = 1 N ( y i − W T x i ) 2 2 σ 2 ⇔ a r g m i n W ∑ i = 1 N ( y i − W T x i ) 2 \begin{array}{l}\hat W&=arg\underset {W}{max}\ L(W)\\ &=arg\underset {W}{max}\ \displaystyle\sum^N_{i=1}{\log{{1\over \sqrt{2\pi}\sigma}-{(y_i-W^Tx_i)^2\over 2\sigma^2}}}\\ & \Leftrightarrow arg\underset {W}{max}\ \displaystyle\sum^N_{i=1}{-{(y_i-W^Tx_i)^2\over 2\sigma^2}}\\ & \Leftrightarrow arg\underset {W}{min}\ \displaystyle\sum^N_{i=1}{{(y_i-W^Tx_i)^2\over 2\sigma^2}}\\ & \Leftrightarrow arg\underset {W}{min}\ \displaystyle\sum^N_{i=1}{(y_i-W^Tx_i)^2} \end{array} W^=argWmax L(W)=argWmax i=1∑Nlog2πσ1−2σ2(yi−WTxi)2⇔argWmax i=1∑N−2σ2(yi−WTxi)2⇔argWmin i=1∑N2σ2(yi−WTxi)2⇔argWmin i=1∑N(yi−WTxi)2- 此结果与最小二乘估计中的loss function求解 W W W的结果一模一样,因此从概率角度用MLE求解与用最小二乘法LSE的本质一样。
- 也因此可以得出,最小二乘估计隐含了一个噪声服从正态分布的假设:
L S E ( 最 小 二 乘 估 计 ) ⇔ M L E ( n o i s e i s G a u s s i a n D i s t r i b u t i o n ) ( 极 大 似 然 估 计 ) \color{red}LSE(最小二乘估计) \Leftrightarrow MLE(noise\;is\;Gaussian\;Distribution)(极大似然估计) LSE(最小二乘估计)⇔MLE(noiseisGaussianDistribution)(极大似然估计)
3. 正则化-岭回归
3.1 过拟合
- 数据
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } , x i ∈ R p , y i ∈ R , i = 1 , 2 , ⋯ , N D=\left \{(x_{1},y_{1}),(x_{2},y_{2}),\cdots ,(x_{N},y_{N})\right \}, x_{i}\in \mathbb{R}^{p},y_{i}\in \mathbb{R},i=1,2,\cdots ,N D={(x1,y1),(x2,y2),⋯,(xN,yN)},xi∈Rp,yi∈R,i=1,2,⋯,N
X = ( x 1 , x 1 , ⋯ , x N ) T = ( x 1 T x 2 T ⋮ x N T ) = ( x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x N 1 x N 2 ⋯ x N p ) N × p Y = ( y 1 y 2 ⋮ y N ) N × 1 X=(x_{1},x_{1},\cdots ,x_{N})^{T}=\begin{pmatrix} x_{1}^{T}\\ x_{2}^{T}\\ \vdots \\ x_{N}^{T} \end{pmatrix}=\begin{pmatrix} x_{11} & x_{12} & \cdots &x_{1p} \\ x_{21} & x_{22}& \cdots &x_{2p} \\ \vdots & \vdots & \ddots &\vdots \\ x_{N1}& x_{N2} & \cdots & x_{Np} \end{pmatrix}_{N \times p}\;Y=\begin{pmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{N} \end{pmatrix}_{N \times 1} X=(x1,x1,⋯,xN)T=⎝⎜⎜⎜⎛x1Tx2T⋮xNT⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11x21⋮xN1x12x22⋮xN2⋯⋯⋱⋯x1px2p⋮xNp⎠⎟⎟⎟⎞N×pY=⎝⎜⎜⎜⎛y1y2⋮yN⎠⎟⎟⎟⎞N×1 - 最小二乘估计
求解: L ( W ) = ∑ i = 1 N ∥ W T x i − y i ∥ 2 L(W)=\displaystyle\sum^{N}_{i=1}{\Vert W^Tx_i-y_i\Vert}^2 L(W)=i=1∑N∥WTxi−yi∥2
得到: W ^ = a r g m i n W L ( W ) ; W ^ = ( X T X ) − 1 X T Y \hat W=arg\underset {W}{min}L(W);\;\hat W=(X^TX)^{-1}X^TY W^=argWminL(W);W^=(XTX)−1XTY - 过拟合
- X X X为 N × p N\times p N×p,即 N N N个样本,每个样本有 p p p维,通常处理时,需要 N ≫ p N \gg p N≫p。
- 实际问题中可能出现数据样本少,或数据的特征过多,使得 N ≫ p N \gg p N≫p不满足,当出现高维小样本的情况即维度 p p p大于样本数 N N N时, X T X X^{T}X XTX就不可逆。
- W ^ = ( X T X ) − 1 X T Y \hat W=(X^TX)^{-1}X^TY W^=(XTX)−1XTY就不能进行求解,这种时候就容易出现过拟合的情况。
- 处理过拟合
处 理 过 拟 合 → { 1. 加 数 据 2. 降 维 / 特 征 选 择 / 特 征 提 取 ( P C A ) 3. 正 则 化 \color{red}处理过拟合\rightarrow \begin{cases} 1. 加数据\\ 2. 降维/特征选择/特征提取(PCA)\\ 3. 正则化 \end{cases} 处理过拟合→⎩⎪⎨⎪⎧1.加数据2.降维/特征选择/特征提取(PCA)3.正则化
3.2 正则化
-
正则化框架
正则化框架: L ( W ) + λ P ( W ) \color{red}L(W)+\lambda P(W) L(W)+λP(W)其中 L L L 为Loss Function, P P P为penalty(惩罚函数)
目标:
a r g m i n W [ L ( W ) + λ P ( W ) ] arg \underset{W}{min}[L(W)+\lambda P(W)] argWmin[L(W)+λP(W)]正则化方式:
{ L 1 正 则 化 ( L a s s o ) : P ( w ) = ∥ W ∥ 1 L 2 正 则 化 ( R i d g e ) : P ( w ) = ∥ W ∥ 2 2 = W T W \color{red}\left\{\begin{matrix} L1正则化(Lasso):P(w)=\left \| W\right \|_{1}\\ L2正则化(Ridge):P(w)=\left \| W\right \|_{2}^{2}=W^TW \end{matrix}\right. {L1正则化(Lasso):P(w)=∥W∥1L2正则化(Ridge):P(w)=∥W∥22=WTW
即: L 1 : a r g m i n W L ( W ) + λ ∣ ∣ W ∣ ∣ 1 , λ > 0 L 2 : a r g m i n W L ( W ) + λ ∣ ∣ W ∣ ∣ 2 2 , λ > 0 \begin{array}{r}L1&:\mathop{argmin}\limits_WL(W)+\lambda||W||_1,\lambda\gt0\\ L2&:\mathop{argmin}\limits_WL(W)+\lambda||W||^2_2,\lambda \gt 0\end{array} L1L2:WargminL(W)+λ∣∣W∣∣1,λ>0:WargminL(W)+λ∣∣W∣∣22,λ>0
本节主要介绍L2 岭回归,也称权值衰减。 -
L1 正则化
L1正则化可以引起稀疏解。
从最小化损失的角度看,由于 L1 项求导在0附近的左右导数都不是0,因此更容易取到0解。从另一个方面看,L1 正则化相当于:
a r g m i n W L ( W ) s . t . ∣ ∣ W ∣ ∣ 1 < C \mathop{argmin}\limits_WL(W)\\ s.t. ||W||_1\lt C WargminL(W)s.t.∣∣W∣∣1<C
我们已经看到平方误差损失函数在 W W W 空间是一个椭球,因此上式求解就是椭球和 ∣ ∣ W ∣ ∣ 1 = C ||W||_1=C ∣∣W∣∣1=C的切点,因此更容易相切在坐标轴上。 -
L2正则化
L2正则化的求解过程:
J ( W ) = ∑ i = 1 N ∥ W T x i − y i ∥ 2 + λ W T W = ( W T X T − Y T ) ( X W − Y ) + λ W T W ⇒ W T X T X W − Y T X W − W T X T Y + λ W T W = W T X T X W − 2 W T X T Y + λ W T W = W T ( X T X + λ I ) W − 2 W T X T Y \begin{array}{r} J(W)&=\displaystyle\sum^{N}_{i=1}{\Vert W^Tx_i-y_i\Vert}^2+\lambda W^TW\\ &=(W^TX^T-Y^T)(XW-Y)+\lambda W^TW\\ &\Rightarrow W^TX^TXW-Y^TXW-W^TX^TY+\lambda W^TW\\ &=W^TX^TXW-2W^TX^TY+\lambda W^TW\\ &=W^T(X^TX+\lambda I)W-2W^TX^TY \end{array} J(W)=i=1∑N∥WTxi−yi∥2+λWTW=(WTXT−YT)(XW−Y)+λWTW⇒WTXTXW−YTXW−WTXTY+λWTW=WTXTXW−2WTXTY+λWTW=WT(XTX+λI)W−2WTXTY
令: ∂ J ( W ) ∂ W = 2 ( X T X + λ I ) W − 2 X T Y = 0 {\partial J(W)\over \partial W}=2(X^TX+\lambda I)W-2X^TY=0 ∂W∂J(W)=2(XTX+λI)W−2XTY=0
则: W ^ = ( X T X + λ I ) − 1 X T Y \hat W = (X^TX+\lambda I)^{-1}X^TY W^=(XTX+λI)−1XTY
- 其中 X T X X^TX XTX 为半正定,当加上 λ I \lambda I λI后必然正定,即可逆;
- 从数学角度上看,其可逆;同时抑制了过拟合的可能性。
4. 正则化-岭回归+贝叶斯角度-高斯噪声高斯先验-MAP
4.1 贝叶斯角度-MAP(最大后验估计)
-
贝叶斯公式
贝叶斯派认为 θ \theta θ也是一个 先 验 的 随 机 变 量 \color{red}先验的随机变量 先验的随机变量,并且 θ ∼ p ( θ ) \theta\sim p\left (\theta \right ) θ∼p(θ),其中 p ( θ ) p\left (\theta \right ) p(θ)是一个 先 验 概 率 \color{red}先验概率 先验概率。我们知道贝叶斯公式如下:
P ( θ ∣ X ) = P ( X ∣ θ ) ⋅ P ( θ ) P ( X ) P(\theta |X)=\frac{P(X|\theta)\cdot P(\theta )}{P(X)} P(θ∣X)=P(X)P(X∣θ)⋅P(θ)
P ( X ) = ∫ θ P ( X , θ ) d θ = ∫ θ P ( X ∣ θ ) ⋅ P ( θ ) d θ P(X)=\int_{\theta}^{}P(X,\theta )d{\theta }=\int_{\theta}^{}P(X|\theta )\cdot P(\theta )d{\theta } P(X)=∫θP(X,θ)dθ=∫θP(X∣θ)⋅P(θ)dθ
P ( θ ∣ X ) = P ( X ∣ θ ) ⋅ P ( θ ) ∫ θ P ( X ∣ θ ) ⋅ P ( θ ) d θ P(\theta |X)=\frac{P(X|\theta)\cdot P(\theta )}{\int_{\theta}^{}P(X|\theta )\cdot P(\theta )d{\theta }} P(θ∣X)=∫θP(X∣θ)⋅P(θ)dθP(X∣θ)⋅P(θ)
其中:- P ( θ ∣ X ) P(\theta |X) P(θ∣X)为 后 验 概 率 \color{red}后验概率 后验概率,也就是我们要得到的东西,是最终的参数分布。
- P ( θ ) P(\theta ) P(θ)为 先 验 概 率 \color{red}先验概率 先验概率,指的是在没有观测到任何数据时对 θ \theta θ 的预先判断。
- P ( X ∣ θ ) P(X|\theta) P(X∣θ)为 似 然 \color{red}似然 似然,是假设 θ \theta θ已知后,我们观察到的数据应该是什么样子的。
这里有两点值得注意的地方:
1. 随 着 数 据 量 的 增 加 , 参 数 分 布 会 越 来 越 向 数 据 靠 拢 , 先 验 的 影 响 力 会 越 来 越 小 ; \color{red}1. 随着数据量的增加,参数分布会越来越向数据靠拢,先验的影响力会越来越小; 1.随着数据量的增加,参数分布会越来越向数据靠拢,先验的影响力会越来越小;
2. 如 果 先 验 是 u n i f o r m d i s t r i b u t i o n ( 均 匀 分 布 ) , 则 贝 叶 斯 方 法 等 价 于 频 率 方 法 。 \color{red}2. 如果先验是uniform distribution(均匀分布),则贝叶斯方法等价于频率方法。 2.如果先验是uniformdistribution(均匀分布),则贝叶斯方法等价于频率方法。 因为直观上来讲,先验是uniform distribution本质上表示对事物没有任何预判。 -
MAP
MAP为贝叶斯学派常用的参数估计方法,他们认为模型参数服从某种潜在分布。可以参考:极大似然估计与最大后验概率估计。- 其首先对参数有一个预先估计,然后根据所给数据,对预估计进行不断调整,因此同一事件,先验不同则事件状态不同。
- 先验假设较为靠谱时有显著的效果。
- 当数据较少时,先验对模型的参数有主导作用,随着数据的增加,真实数据样例将占据主导地位。
-
贝叶斯角度模型建立
- 我们知道 f ( W ) = W T X f(W)=W^TX f(W)=WTX是线性回归的结果。
- 我们从第二节概率视角-高斯噪声-MLE对 y y y预先估计: y = f ( W ) + ϵ = W T X + ϵ y=f(W)+\epsilon=W^TX+\epsilon y=f(W)+ϵ=WTX+ϵ
与第二节一样, ϵ \epsilon ϵ为噪声 ( ϵ ∼ N ( 0 , σ 2 ) ) \color{red}(\epsilon\sim N(0,\sigma^2)) (ϵ∼N(0,σ2));并且 y ∣ X ; W ∼ N ( W T X , σ 2 ) \color{red}y|X;W \sim N(W^TX,\sigma^2) y∣X;W∼N(WTX,σ2)。
- 从MAP的角度来看,参数 W W W必然服从某个分布,故假设 W ∼ N ( 0 , σ 0 2 ) \color{red}W\sim N(0, \sigma^2_0) W∼N(0,σ02)
我们的目标: W ^ = a r g m a x W p ( W ∣ y ) \hat W = arg\underset{W}{max}\ \ p(W|y) W^=argWmax p(W∣y)
4.2 求解 W W W
- 已知条件
首先根据条件概率可得 p ( W ∣ y ) = p ( y ∣ W ) ⋅ p ( W ) p ( y ) \color{blue}p(W|y)= {p(y|W)\cdot p(W)\over p(y)} p(W∣y)=p(y)p(y∣W)⋅p(W)
由于已知 y ∣ X ; W y|X;W y∣X;W 和 W W W 的分布,因此可得:
p ( y ∣ W ) = 1 2 π σ exp { − ( y − W T X ) 2 2 σ 2 } ( 似 然 ) p(y|W)={1\over\sqrt{2\pi}\sigma}\exp{\{-{(y-W^TX)^2\over2\sigma^2}\}}\color{blue}(似然) p(y∣W)=2πσ1exp{−2σ2(y−WTX)2}(似然)
p ( W ) = 1 2 π σ 0 exp { − ∥ W ∥ 2 2 σ 0 2 } ( 先 验 ) p(W)={1\over\sqrt{2\pi}\sigma_0}\exp{\{-{\Vert W\Vert^2\over2\sigma_0^2}\}}\color{blue}(先验) p(W)=2πσ01exp{−2σ02∥W∥2}(先验) - 求解 W ( 后 验 ) W\color{blue}(后验) W(后验)
W ^ = a r g m a x W p ( y ∣ W ) p ( W ) p ( y ) ⇒ a r g m a x W p ( y ∣ W ) p ( W ) = a r g m a x W log { p ( y ∣ W ) p ( W ) } = a r g m a x W log { 1 2 π σ exp { − ( y − W T X ) 2 2 σ 2 } 1 2 π σ 0 exp { − ∥ W ∥ 2 2 σ 0 2 } } = a r g m a x W log ( 1 2 π σ 1 2 π σ 0 ) − ( y − W T X ) 2 2 σ 2 − ∥ W ∥ 2 2 σ 0 2 ⇒ a r g m a x W − ( y − W T X ) 2 2 σ 2 − ∥ W ∥ 2 2 σ 0 2 = a r g m i n W ( y − W T X ) 2 2 σ 2 + ∥ W ∥ 2 2 σ 0 2 ⇒ a r g m i n W ( y − W T X ) 2 + σ 2 σ 0 2 ∥ W ∥ 2 = a r g m i n W ∑ i = 1 N ( y i − W T x i ) 2 + σ 2 σ 0 2 ∥ W ∥ 2 \begin{array}{l} \hat W &= arg\underset{W}{max}\ \ {p(y|W)p(W)\over p(y)}\Rightarrow arg\underset{W}{max}\ \ p(y|W)p(W)\\ &=arg\underset{W}{max}\ \ \log{\{p(y|W)p(W) \}}\\ &=arg\underset{W}{max}\ \ \log{\{{1\over\sqrt{2\pi}\sigma}\exp{\{-{(y-W^TX)^2\over2\sigma^2}\}}{1\over\sqrt{2\pi}\sigma_0}\exp{\{-{\Vert W\Vert^2\over2\sigma_0^2}\}}\}}\\ &=arg\underset{W}{max}\ \ \log{({1\over\sqrt{2\pi}\sigma}{1\over\sqrt{2\pi}\sigma_0})}-{(y-W^TX)^2\over2\sigma^2}-{\Vert W\Vert^2\over2\sigma_0^2}\\ &\Rightarrow arg\underset{W}{max}\ \ -{(y-W^TX)^2\over2\sigma^2}-{\Vert W\Vert^2\over2\sigma_0^2}\\ &=arg\underset{W}{min}\ \ {(y-W^TX)^2\over2\sigma^2}+{\Vert W\Vert^2\over2\sigma_0^2}\\ &\Rightarrow arg\underset{W}{min}\ \ (y-W^TX)^2+{\sigma^2\over \sigma^2_0}\Vert W \Vert ^2\\ &=arg\underset{W}{min}\ \ \sum^N_{i=1}(y_i-W^Tx_i)^2+{\sigma^2\over \sigma^2_0}\Vert W \Vert ^2\\ \end{array} W^=argWmax p(y)p(y∣W)p(W)⇒argWmax p(y∣W)p(W)=argWmax log{p(y∣W)p(W)}=argWmax log{2πσ1exp{−2σ2(y−WTX)2}2πσ01exp{−2σ02∥W∥2}}=argWmax log(2πσ12πσ01)−2σ2(y−WTX)2−2σ02∥W∥2⇒argWmax −2σ2(y−WTX)2−2σ02∥W∥2=argWmin 2σ2(y−WTX)2+2σ02∥W∥2⇒argWmin (y−WTX)2+σ02σ2∥W∥2=argWmin ∑i=1N(yi−WTxi)2+σ02σ2∥W∥2
观察上式结果,其与加了Ridge正则化的Loss Function一致: J ( W ) = ∑ i = 1 N ∥ W T x i − y i ∥ 2 + λ W T W J(W)=\displaystyle\sum^{N}_{i=1}{\Vert W^Tx_i-y_i\Vert}^2+\lambda W^TW J(W)=i=1∑N∥WTxi−yi∥2+λWTW
其中 λ = σ 2 σ 0 2 \lambda = {\sigma^2\over \sigma^2_0} λ=σ02σ2
所以 r e g u l a r i z e d L S E ⇔ M A P ( n o i s e 为 G u a s s i a n D i s t r i b u t i o n ; P r i o r 为 G u a s s i a n D i s t r i b u t i o n ) \color{red}regularized\ \ LSE \Leftrightarrow MAP(noise为Guassian \ Distribution;Prior为Guassian \ Distribution) regularized LSE⇔MAP(noise为Guassian Distribution;Prior为Guassian Distribution)
5. 小结
-
线性回归模型是最简单的模型,但是麻雀虽小,五脏俱全,在这里,我们利用最小二乘误差得到了闭式解。同时也发现,在噪声为高斯分布的时候,MLE 的解等价于最小二乘误差,而增加了正则项后,最小二乘误差加上 L2 正则项等价于高斯噪声先验下的 MAP解,加上 L1 正则项后,等价于 Laplace 噪声先验。
L S E ⇔ M L E ( n o i s e 为 G a u s s i a n D i s t r i b u t i o n ) R e g u l a r i z e d L S E ⇔ M A P ( n o i s e , p r i o r 为 G a u s s i a n D i s t r i b u t i o n ) \color{red}LSE\Leftrightarrow MLE(noise为Gaussian Distribution)\\ Regularized \: LSE\Leftrightarrow MAP(noise,prior为Gaussian Distribution) LSE⇔MLE(noise为GaussianDistribution)RegularizedLSE⇔MAP(noise,prior为GaussianDistribution) -
传统的机器学习方法或多或少都有线性回归模型的影子:
- 线性模型往往不能很好地拟合数据,因此有三种方案克服这一劣势:
- 对特征的维数进行变换,例如多项式回归模型就是在线性特征的基础上加入高次项。
- 在线性方程后面加入一个非线性变换,即引入一个非线性的激活函数,典型的有线性分类模型如感知机。
- 对于一致的线性系数,我们进行多次变换,这样同一个特征不仅仅被单个系数影响,例如多层感知机(深度前馈网络)。
- 线性回归在整个样本空间都是线性的,我们修改这个限制,在不同区域引入不同的线性或非线性,例如线性样条回归和决策树模型。
- 线性回归中使用了所有的样本,但是对数据预先进行加工学习的效果可能更好(所谓的维数灾难,高维度数据更难学习),例如 PCA 算法和流形学习。
参考
- 线性回归|机器学习推导系列(三)
- 机器学习-白板推导系列(三)-线性回归(Linear Regression) 笔记
- 线性回归
- 极大似然估计与最大后验概率估计
- 第十六讲 投影矩阵(Ax=b)和最小二乘法