吴恩达深度神经网络笔记—神经风格转换
目标
实现神经风格转换算法
用算法生成新的艺术图像
导包
import time
import os
import sys
import scipy.io
import scipy.misc
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
from PIL import Image
import nst_utils
import numpy as np
import tensorflow as tf
%matplotlib inline
神经风格转换描述
神经风格转换(Neural Style Transfer,NST)是深学习中最有趣的技术之一。如下图所示,它合并两个图像,即“内容”图像(Content)和“风格”图像(Style),以创建“生成的”图像(Generated)。生成的图像G将图像C的“内容”与图像S的“风格”相结合。
如图:

迁移学习
使用先前训练好了的卷积网络,并在此基础之上进行构建。使用在不同任务上训练的网络并将其应用于新任务的想法称为迁移学习。
使用VGG-19网络模型,这个模型已经在非常大的ImageNet数据库上进行了训练,因此学会了识别各种低级特征(浅层)和高级特征(深层)。
从VGG模型加载参数。
model = nst_utils.load_vgg_model("pretrained-model/imagenet-vgg-verydeep-19.mat")
print(model)
结果:
{‘input’:
, ‘conv1_1’: , ‘conv1_2’: , ‘avgpool1’: , ‘conv2_1’: , ‘conv2_2’: , ‘avgpool2’: , ‘conv3_1’: , ‘conv3_2’: , ‘conv3_3’: , ‘conv3_4’: , ‘avgpool3’: , ‘conv4_1’: , ‘conv4_2’: , ‘conv4_3’: , ‘conv4_4’: , ‘avgpool4’: , ‘conv5_1’: , ‘conv5_2’: , ‘conv5_3’: , ‘conv5_4’: , ‘avgpool5’: }
该模型存储在一个python字典中,其中每个变量名都是键,相应的值是一个包含该变量值的张量,要通过此网络运行图像,只需将图像提供给模型。 在TensorFlow中,你可以使用tf.assign函数来做到这一点:
model["input"].assign(image)
这将图像作为输入给模型,在此之后,如果想要访问某个特定层的激活,比如4_2,请这样做:
sess.run(model["conv4_2"])
转换步骤
- 构建内容损失函数(,)
- 构建风格损失函数(,)
- 它放在一起得到()=(,)+(,)
内容损失函数
本例中采用卢浮宫做内容图像C
content_image = scipy.misc.imread("images/louvre.jpg")
imshow(content_image)
如何确保生成的图像G与图像C的内容匹配
浅层的一个卷积网络往往检测到较低层次的特征,如边缘和简单的纹理,更深层往往检测更高层次的特征,如更复杂的纹理以及对象分类等。
我们希望“生成的”图像G具有与输入图像C相似的内容。假设我们选择了一些层的激活来表示图像的内容,在实践中,如果你在网络中间选择一个层——既不太浅也不太深,你会得到最好的的视觉结果。
将图像C作为已经训练好的VGG网络的输入,然后进行前向传播。让aC成为你选择的层中的隐藏层激活,激活值为 n H × n W × n C 的张量。然后用图像G重复这个过程:将G设置为输入数据,并进行前向传播,让 a (G)成为相应的隐层激活,我们将把内容成本函数定义为:
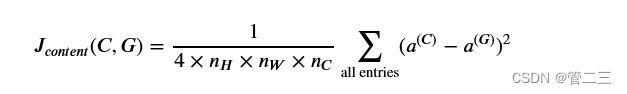
这里nH,nW,nC分别代表了你选择的隐藏层的高度、宽度、通道数,并出现在成本的归一化项中,为了使得方便理解,需要注意的是aC是与隐藏层激活相对应的卷积值,为了计算成本(,),可以方便地将这些3D卷积展开为2D矩阵,如下所示。
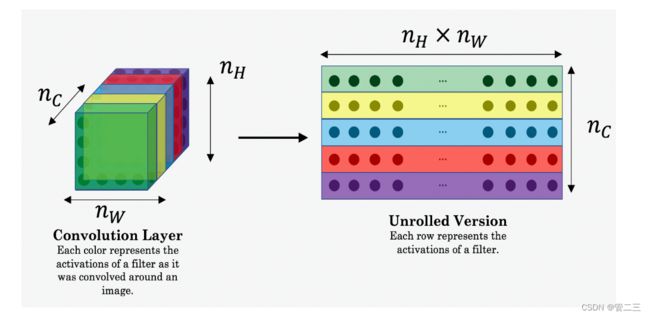
使用tensorflow来实现内容代价函数,它由以下3步构成:
- 从a_G中获取维度信息:
从张量X中获取维度信息,可以使用:X.get_shape().as_list() - 将a_C与a_G如上图一样降维
- 计算内容代价
def compute_content_cost(a_C, a_G):
m, n_H, n_W, n_C = a_G.get_shape().as_list()
a_C_unrolled = tf.transpose(tf.reshape(a_C, [n_H * n_W, n_C]))
a_G_unrolled = tf.transpose(tf.reshape(a_G, [n_H * n_W, n_C]))
J_content = 1/(4*n_H*n_W*n_C)*tf.reduce_sum(tf.square(tf.subtract(a_C_unrolled, a_G_unrolled)))
return J_content
测试:
tf.reset_default_graph()
with tf.Session() as test:
tf.set_random_seed(1)
a_C = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
a_G = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
J_content = compute_content_cost(a_C, a_G)
print("J_content = " + str(J_content.eval()))
test.close()
结果:
J_content = 6.76559
注意点:
- 内容成本采用神经网络的隐层激活,并测量a( C ) a( G )的区别。
- 当我们以后最小化内容成本时,这将有助于确保 G 的内容与 C 相似。
风格损失函数
本例中的风格图像S如下
style_image = scipy.misc.imread("images/monet_800600.jpg")
imshow(style_image)
如何定义“style”常量函数(,):
样式矩阵也称为“Gram矩阵”。在线性代数中,一组向量(v1,…,vn)的Gram矩阵G是点积矩阵,其条目为Gij=viTvj=np.dot(vi,vj)。换句话说,Gij比较了相似程度
vi到vj:如果它们高度相似,你会期望它们有一个大的点积,因此Gij会很大。
请注意,这里使用的变量名中有一个不幸的冲突。我们遵循文献中使用的常用术语,但G用于表示Style矩阵(或Gram矩阵)以及生成的图像G。
在NST中,您可以通过将“展开”过滤器矩阵与其转置相乘来计算样式矩阵:
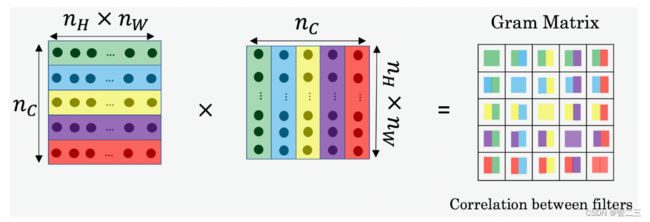
结果是维度(nC,nC)的矩阵,其中nC是滤波器的数量。值Gij测量滤波器i的激活与滤波器j的激活的相似程度。
gram矩阵的一个重要部分是,对角线元素(如Gii)也测量滤波器i的活跃程度。例如,假设滤波器i检测图像中的垂直纹理。然后Gii测量整个图像中垂直纹理的常见程度:如果Gii很大,这意味着图像有很多垂直纹理。
通过捕获不同类型的特征(Gii)的流行程度以及一起出现的不同特征(Gij),样式矩阵G测量图像的样式。
def gram_matrix(A):
GA = tf.matmul(A,tf.transpose(A))
return GA
测试:
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as test:
tf.compat.v1.set_random_seed(1)
A = tf.compat.v1.random_normal([3, 2*1], mean=1, stddev=4)
GA = gram_matrix(A)
print("GA = " + str(GA.eval()))
结果:
GA = [[ 15.615461 12.248833 -29.87157 ]
[ 12.248833 10.877857 -19.879116]
[-29.87157 -19.879116 67.08007 ]]
生成样式矩阵(Gram矩阵)后,您的目标将是最小化“样式”图像S的Gram矩阵与“生成”图像G的Gram矩阵之间的距离。目前,我们仅使用单个隐藏层a[l],该层的相应样式成本定义为:
() 和() 分别是使用网络中特定隐藏层的隐藏层激活计算的“样式”图像和“生成”图像的Gram矩阵。
使用tensorflow来实现样式代价函数,它由以下4步构成:
- 从隐藏层激活中检索尺寸a_G:
要从张量X中检索维度,请使用:X.get_shape().as_list() - 将隐藏层激活a_S和a_G展开为2D矩阵,如上图所示。
- 计算图像S和G的样式矩阵(使用之前编写的函数)
- 计算样式损失函数
def compute_layer_style_cost(a_S, a_G):
m, n_H, n_W, n_C = a_G.get_shape().as_list()
a_Sres = tf.transpose(tf.reshape(a_S,[n_C, n_H*n_W]))
a_Gres = tf.transpose(tf.reshape(a_G,[n_C, n_H*n_W]))
#矩阵转置的时候一定要注意方向
a_S_Gram = gram_matrix(a_Sres)
a_G_Gram = gram_matrix(a_Gres)
J_style_layer = tf.reduce_sum(tf.square(tf.subtract(a_S_Gram,a_G_Gram)))/(4*n_C*n_C*(n_H*n_W)*(n_H*n_W))
return J_style_layer
测试:
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as test:
tf.compat.v1.set_random_seed(1)
a_S = tf.compat.v1.random_normal([1, 4, 4, 3], mean=1, stddev=4)
a_G = tf.compat.v1.random_normal([1, 4, 4, 3], mean=1, stddev=4)
J_style_layer = compute_layer_style_cost(a_S, a_G)
print("J_style_layer = " + str(J_style_layer.eval()))
结果:
J_style_layer = 58.384556
样式权重
到目前为止,您只从一个图层中捕捉到了样式。如果我们从几个不同的层“合并”样式成本,我们将获得更好的结果。完成此练习后,请随时回来尝试不同的权重,看看它如何改变生成的图像. 但就目前而言,这是一个相当合理的默认值:
STYLE_LAYERS = [
('conv1_1', 0.2),
('conv2_1', 0.2),
('conv3_1', 0.2),
('conv4_1', 0.2),
('conv5_1', 0.2)]
可以按如下方式组合不同图层的样式成本:
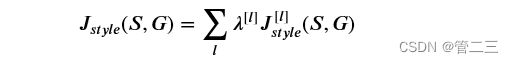
我们实现了compute_style_cost(…)函数。它只需多次调用compute_layer_style_cost(…),并使用style_LAYERS中的值对其结果进行加权。仔细阅读它,确保你明白它在做什么。
def compute_style_cost(model, STYLE_LAYERS):
J_style = 0
for layer_name, coeff in STYLE_LAYERS:
out = model[layer_name]
a_S = sess.run(out)
a_G = out
J_style_layer = compute_layer_style_cost(a_S, a_G)
J_style += coeff * J_style_layer
return J_style
在上面的for循环的内循环中,a_G是一个张量,尚未计算。当我们在下面的model_nn()中运行TensorFlow图时,它将在每次迭代时进行评估和更新。
定义要优化的总成本
最后,让我们创建一个最小化样式和内容成本的成本函数。公式为:
![]()
def total_cost(J_content, J_style, alpha = 10, beta = 40):
J = alpha*J_content+beta*J_style
return J
测试:
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as test:
np.random.seed(3)
J_content = np.random.randn()
J_style = np.random.randn()
J = total_cost(J_content, J_style)
print("J = " + str(J))
结果:
J = 35.34667875478276
解决优化问题
最后,让我们一起来实现神经风格转换!
以下是该程序必须执行的操作:
- 创建交互式会话
- 加载内容图像
- 加载样式图像
- 随机初始化要生成的图像
- 加载VGG16模型
- 构建TensorFlow图:
通过VGG16模型运行内容映像并计算内容成本
通过VGG16模型运行样式图像并计算样式成本
计算总成本
定义优化器和学习率 - 初始化TensorFlow图并运行大量迭代,每一步都更新生成的图像。
让我们详细了解各个步骤。
您之前已经实施了总体成本(). 我们现在将设置TensorFlow,以优化. 为此,您的程序必须重置图形并使用“交互式会话”。与常规会话不同,“交互式会话”将自己安装为构建图形的默认会话。这允许您运行变量,而无需经常引用会话对象,从而简化了代码。
tf.compat.v1.reset_default_graph()
sess = tf.compat.v1.InteractiveSession()
让我们加载、重塑和规范我们的“内容”形象(卢浮宫博物馆图片):
content_image = imageio.v2.imread("images/louvre_small.jpg")
imshow(content_image)
content_image = reshape_and_normalize_image(content_image)
让我们加载、重塑和规范我们的“风格”形象(克劳德·莫奈的绘画):
style_image = imageio.v2.imread("images/monet.jpg")
imshow(style_image)
style_image = reshape_and_normalize_image(style_image)
现在,我们将“生成的”图像初始化为从content_image创建的噪声图像。通过将生成的图像的像素初始化为主要是噪声,但仍然与内容图像略微相关,这将帮助“生成的”图像的内容更快地匹配“内容”图像的属性。
generated_image = generate_noise_image(content_image)
imshow(generated_image[0])
model = load_vgg_model("pretrained-model/imagenet-vgg-verydeep-19.mat")
为了让程序计算内容成本,我们现在将分配a_C和a_G作为适当的隐藏层激活。我们将使用层conv4_2来计算内容成本。以下代码执行以下操作:
将内容图像指定为VGG模型的输入。
将a_C设置为为层“conv4_2”提供隐藏层激活的张量。
将a_G设置为为同一层提供隐藏层激活的张量。
使用a_C和a_G计算内容成本。
sess.run(model['input'].assign(content_image))
out = model['conv4_2']
a_C = sess.run(out)
a_G = out
J_content = compute_content_cost(a_C, a_G)
此时,a_G是一个张量,尚未计算。当我们在下面的model_nn()中运行Tensorflow图时,它将在每次迭代时进行评估和更新。
sess.run(model['input'].assign(style_image))
J_style = compute_style_cost(model, STYLE_LAYERS)
现在有了J_content和J_style,通过调用total_cost()来计算总成本J。使用alpha=10和beta=40。
J = total_cost(J_content,J_style,alpha = 10,beta = 40)
您以前学习过如何在TensorFlow中设置Adam优化器。让我们在这里使用2.0的学习率来实现这一点
optimizer = tf.compat.v1.train.AdamOptimizer(2.0)
train_step = optimizer.minimize(J)
实现model_nn()函数,该函数初始化tensorflow图的变量,将输入图像(初始生成的图像)指定为VGG16模型的输入,并运行大量步骤的train_step。
def model_nn(sess, input_image, num_iterations = 200):
sess.run(tf.compat.v1.global_variables_initializer())
sess.run(model['input'].assign(input_image))
for i in range(num_iterations):
sess.run(train_step)
g_image = sess.run(model['input'])
if i%20 == 0:
Jt, Jc, Js = sess.run([J, J_content, J_style])
print("Iteration " + str(i) + " :")
print("total cost = " + str(Jt))
print("content cost = " + str(Jc))
print("style cost = " + str(Js))
save_image("output/" + str(i) + ".png", generated_image)
save_image('output/generated_image.jpg', generated_image)
return generated_image
运行以下单元格以生成艺术图像。每20次迭代需要大约3分钟的CPU时间,但在之后,您就会开始观察到有吸引力的结果≈140次迭代。神经风格转换通常使用GPU进行训练
model_nn(sess, generated_image)
 运行此操作后,在笔记本的上栏中单击“文件”,然后单击“打开”。转到“/output”目录以查看所有保存的图像。打开“generated_image”查看生成的图像!:)
运行此操作后,在笔记本的上栏中单击“文件”,然后单击“打开”。转到“/output”目录以查看所有保存的图像。打开“generated_image”查看生成的图像!:)
您应该可以看到下图右侧的内容:






