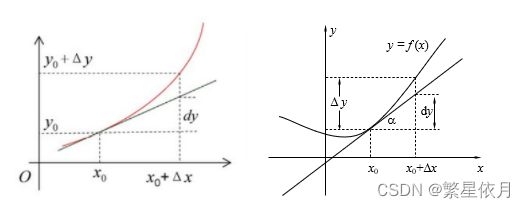高等数学笔记-乐经良老师-第三章-导数和微分
高等数学笔记-乐经良老师
第三章 导数和微分
第一节 导数的概念
一、例子
01 速度
运动物体的路程函数 S ( t ) S(t) S(t),时间从 t 0 → t 0 + Δ t t_{0} \rightarrow t_{0}+\Delta t t0→t0+Δt,路程 Δ S = S ( t 0 + Δ t ) − S ( t 0 ) \Delta S=S\left(t_{0}+\Delta t\right)-S\left(t_{0}\right) ΔS=S(t0+Δt)−S(t0)
平 均 速 度 : Δ S Δ t t 0 时 刻 的 瞬 时 速 度 : lim Δ t → 0 Δ S Δ t = lim Δ t → 0 S ( t 0 + Δ t ) − S ( t 0 ) Δ t \begin{aligned} & 平均速度: \frac{\Delta S}{\Delta t} \\ & t_{0} 时刻的瞬时速度:\\ & \quad\quad \lim _{\Delta t \rightarrow 0} \frac{\Delta S}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{S\left(t_{0}+\Delta t\right)-S\left(t_{0}\right)}{\Delta t} \end{aligned} 平均速度:ΔtΔSt0时刻的瞬时速度:Δt→0limΔtΔS=Δt→0limΔtS(t0+Δt)−S(t0)
02 斜率
求函数曲线 y = f ( x ) y=f(x) y=f(x) 上点 M 0 ( x 0 , y 0 ) M_{0}\left(x_{0}, y_{0}\right) M0(x0,y0) 处的切线。
设 M 0 M M_0M M0M 是过 M 0 M_0 M0 点的割线,沿曲线 M → M 0 M \rightarrow M_0 M→M0 割线极限位置的直线,即切线。
割线斜率:
Δ y Δ x = f ( x 0 + Δ x ) − f ( x 0 ) Δ x \ \frac{\Delta y}{\Delta x}=\frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} ΔxΔy=Δxf(x0+Δx)−f(x0)
切线斜率:
lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x \ \lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0)
03 线密度
横截面很小 ( 为一个单位 ) 的细线棒,置于数轴上原点左侧,从 0 点到 x x x 点处一段质量为 m ( x ) m(x) m(x),
x 0 → x 0 + Δ x x_{0} \rightarrow x_{0}+\Delta x x0→x0+Δx 一段的平均线密度
Δ m Δ x = m ( x 0 + Δ x ) − m ( x 0 ) Δ x \frac{\Delta m}{\Delta x}=\frac{m\left(x_{0}+\Delta x\right)-m\left(x_{0}\right)}{\Delta x} ΔxΔm=Δxm(x0+Δx)−m(x0)
x 0 x_{0} x0 点的线密度
lim Δ x → 0 Δ m Δ x = lim Δ x → 0 m ( x 0 + Δ x ) − m ( x 0 ) Δ x \lim _{\Delta x \rightarrow 0} \frac{\Delta m}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{m\left(x_{0}+\Delta x\right)-m\left(x_{0}\right)}{\Delta x} Δx→0limΔxΔm=Δx→0limΔxm(x0+Δx)−m(x0)
二、定义
01 导数
(1) 导数的定义
若 y = y ( x ) y=y(x) y=y(x) 在 x = x 0 x=x_0 x=x0 的邻域有定义,则
f ′ ( x 0 ) = d e f lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f^{\prime}\left(x_{0}\right)\stackrel{d e f}{=}\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} f′(x0)=defx→x0limx−x0f(x)−f(x0)
称为 y = f ( x ) y=f(x) y=f(x) 在 x 0 x_0 x0 的导数(微商),
自变量增量 Δ x = x − x 0 \Delta x=x-x_0 Δx=x−x0,函数增量 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y=f(x_0+\Delta x)-f(x_0) Δy=f(x0+Δx)−f(x0),也可以用增量的写法:
f ′ ( x 0 ) = lim x → 0 Δ f Δ x f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow 0} \frac{\Delta f}{\Delta x} f′(x0)=x→0limΔxΔf
导数的等价形式:
f ′ ( x 0 ) = lim x → 0 Δ f Δ x = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 = lim x → x 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\lim _{x \rightarrow 0} \frac{\Delta f}{\Delta x}=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}=\lim _{x \rightarrow x_{0}} \frac{f(x_0+\Delta x)-f\left(x_{0}\right)}{\Delta x} f′(x0)=x→0limΔxΔf=x→x0limx−x0f(x)−f(x0)=x→x0limΔxf(x0+Δx)−f(x0)
导数的其他记号(等价表述):
y ′ ( x 0 ) , y ′ ∣ x = x 0 , f ′ ∣ x = x 0 , d f ( x 0 ) d x , d f d x ∣ x = x 0 , d y d x ∣ x = x 0 y'(x_0) \ , \ \left.y^{\prime}\right|_{x=x_{0}} \ , \ \left.f^{\prime}\right|_{x=x_{0}} \ , \ \frac{d f\left(x_{0}\right)}{d x} \ , \ \left.\frac{d f}{d x}\right|_{x=x_{0}} \ , \ \left.\frac{d y}{d x}\right|_{x=x_{0}} y′(x0) , y′∣x=x0 , f′∣x=x0 , dxdf(x0) , dxdf∣∣∣∣x=x0 , dxdy∣∣∣∣x=x0
(2) 导数的几何意义
表述函数曲线 y = y ( x ) y=y(x) y=y(x) 在该点切线的斜率。
(3) 导数不存在的一种情况
当 lim Δ x → 0 Δ f Δ x = ∞ \lim \limits_{\Delta x \rightarrow 0} \frac{\Delta f}{\Delta x}=\infty Δx→0limΔxΔf=∞ 时导数不存在,但可以说导数为 ∞ \infty ∞,此时曲线在该点切线与 x x x 轴垂直。
02 单侧导数
-
左导数与右导数
右 导 数 f + ′ ( x 0 ) = lim Δ x → 0 + Δ f Δ x 左 导 数 f − ′ ( x 0 ) = lim Δ x → 0 − Δ f Δ x \begin{aligned} & 右导数\quad f_{+}^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0^{+}} \frac{\Delta f}{\Delta x}\\ & 左导数\quad f_{-}^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0^{-}} \frac{\Delta f}{\Delta x} \end{aligned} 右导数f+′(x0)=Δx→0+limΔxΔf左导数f−′(x0)=Δx→0−limΔxΔf -
命题
f ′ ( x 0 ) 存 在 ⇒ f + ′ ( x 0 ) , f − ′ ( x 0 ) 存 在 且 相 等 。 f^{\prime}\left(x_{0}\right)\ 存在\quad \Rightarrow \quad f_{+}^{\prime}\left(x_{0}\right),f_{-}^{\prime}\left(x_{0}\right)\ 存在且相等。 f′(x0) 存在⇒f+′(x0),f−′(x0) 存在且相等。 -
小结论
lim h → 0 f ( x 0 + α h ) − f ( x 0 ) h = α f ′ ( x 0 ) \lim _{h \rightarrow 0} \frac{f\left(x_{0}+\alpha h\right)-f\left(x_{0}\right)}{h}=\alpha f^{\prime}\left(x_{0}\right) h→0limhf(x0+αh)−f(x0)=αf′(x0)
03 导函数
y = f ( x ) y=f(x) y=f(x) 在区间 I I I 内每点有导数,在 I I I 的闭端点有单侧导数,
则称函数 f ( x ) f(x) f(x) 在区间 I I I 可导,记为 f ( x ) ∈ D ( I ) f(x) \in \mathrm{D}(I) f(x)∈D(I), f ′ ( x ) f^{\prime}(x) f′(x) 称为 f ( x ) f(x) f(x) 的导函数。
注意,开区间内可导和闭区间上可导。
三、可导与连续的关系
01 可导必连续
Δ f = f ′ ( x ) Δ x + o ( Δ x ) \Delta f=f^{\prime}(x) \Delta x+o(\Delta x) Δf=f′(x)Δx+o(Δx) 增量公式
02 连续未必可导
- 典型例子
- f ( x ) = ∣ x ∣ f(x)=|x| f(x)=∣x∣
- f ( x ) = { x sin 1 x x ≠ 0 0 x = 0 f(x)=\left\{\begin{array}{cc}x \sin \frac{1}{x} & x \neq 0 \\ 0 & x=0\end{array}\right. f(x)={xsinx10x=0x=0
第二节 微分
一、定义
对 y = f ( x ) y=f(x) y=f(x) 考虑增量 Δ y = f ( x + Δ x ) − f ( x ) \Delta y=f(x+\Delta x)-f(x) Δy=f(x+Δx)−f(x) 有增量公式
Δ y = f ′ ( x ) Δ x + o ( Δ x ) \Delta y=f^{\prime}(x) \Delta x+o(\Delta x) Δy=f′(x)Δx+o(Δx)
其中 f ′ ( x ) Δ x f'(x)\Delta x f′(x)Δx 称为线性主部(线性;主要部分)
01 微分
若 y = f ( x ) y=f(x) y=f(x) 在点 x x x 处的增量 Δ y \Delta y Δy 可表示为 Δ y = A Δ x + o ( Δ x ) \Delta y=A \Delta x+o(\Delta x) Δy=AΔx+o(Δx)( A A A 与 Δ x \Delta x Δx 无关,常数)
称 f ( x ) f(x) f(x) 在 x x x 可微, A Δ x A\Delta x AΔx 为 y = f ( x ) y=f(x) y=f(x) 在 x x x 处的微分,记为 d y = A Δ x dy=A\Delta x dy=AΔx .( d y ≈ Δ y dy \approx \Delta y dy≈Δy)
02 可微与可导
- 可微 ⇔ \Leftrightarrow ⇔ 可导,且 d y = f ′ ( x ) Δ x dy=f'(x)\Delta x dy=f′(x)Δx
- 由 d x = Δ x ⇒ d y = f ′ ( x ) d x dx=\Delta x \Rightarrow dy=f'(x)dx dx=Δx⇒dy=f′(x)dx
03 几何意义
函数曲线在垂直方向上的变化用切线在垂直方向的变化代替。
Δ y \Delta y Δy 与 d y dy dy 的几何意义:(1) Δ y \Delta y Δy:函数纵坐标增量;(2) d y dy dy:切线上纵坐标增量。
二、微分的应用
第三节 导数与微分的运算法
一、函数和差积商的导数
若 u ( x ) , v ( x ) ∈ D ( I ) u(x), v(x) \in D(I) u(x),v(x)∈D(I),则 u ( x ) ± v ( x ) , u ( x ) v ( x ) , u ( x ) v ( x ) ( v ( x ) ≠ 0 ) u(x) \pm v(x)\ ,\ u(x) v(x)\ ,\ \frac{u(x)}{v(x)}\ \ (v(x) \neq 0) u(x)±v(x) , u(x)v(x) , v(x)u(x) (v(x)=0) 均在 I I I 可导,
且成立
( 1 ) ( u ( x ) ± v ( x ) ) ′ = u ′ ( x ) ± v ′ ( x ) ( 2 ) ( u ( x ) v ( x ) ) ′ = u ′ ( x ) v ( x ) + u ( x ) v ′ ( x ) ( 3 ) ( u ( x ) v ( x ) ) ′ = u ′ ( x ) v ( x ) − u ( x ) v ′ ( x ) v 2 ( x ) \begin{aligned} & (1)\ \ \ (u(x) \pm v(x))^{\prime}=u^{\prime}(x) \pm v^{\prime}(x) \\ & (2)\ \ \ (u(x) v(x))^{\prime}=u^{\prime}(x) v(x)+u(x) v^{\prime}(x) \\ & (3)\ \ \ \left(\frac{u(x)}{v(x)}\right)^{\prime}=\frac{u^{\prime}(x) v(x)-u(x) v^{\prime}(x)}{v^{2}(x)} \end{aligned} (1) (u(x)±v(x))′=u′(x)±v′(x)(2) (u(x)v(x))′=u′(x)v(x)+u(x)v′(x)(3) (v(x)u(x))′=v2(x)u′(x)v(x)−u(x)v′(x)
特别有
( c u ( x ) ) ′ = c u ′ ( x ) , ( 1 v ( x ) ) ′ = − v ′ ( x ) v 2 ( x ) (c u(x))^{\prime}=c u^{\prime}(x)\ , \ \left(\frac{1}{v(x)}\right)^{\prime}=-\frac{v^{\prime}(x)}{v^{2}(x)} (cu(x))′=cu′(x) , (v(x)1)′=−v2(x)v′(x)
二、反函数的导数
x = f ( y ) x=f(y) x=f(y) 在区间 I I I 严格单调、可导且 f ′ ( y ) ≠ 0 f'(y)\neq0 f′(y)=0,则反函数 y = f − 1 ( x ) y=f^{-1}(x) y=f−1(x) 在对应 y y y 的 x x x 可导,且
( f − 1 ( x ) ) ′ = 1 f ′ ( y ) , 即 d y d x = 1 d x d y 或 y x ′ = 1 x y ′ \left(f^{-1}(x)\right)^{\prime}=\frac{1}{f^{\prime}(y)}\ ,\ 即\ \ \frac{d y}{d x}=\frac{1}{\frac{d x}{d y}} \ \ 或\ \ y_{x}^{\prime}=\frac{1}{x_{y}^{\prime}} (f−1(x))′=f′(y)1 , 即 dxdy=dydx1 或 yx′=xy′1
三、复合函数的导数(链法则)
01 复合函数的导数
u = φ ( x ) u=\varphi(x) u=φ(x) 在 x x x 可导, f ( u ) f(u) f(u) 在对应 x x x 的 u u u 处可导,则复合函数 f ( φ ( x ) ) f(\varphi(x)) f(φ(x)) 在 x x x 可导,且
( f ( φ ( x ) ) ) ′ = f ′ ( u ) φ ′ ( x ) = f ′ ( φ ( x ) ) φ ′ ( x ) (f(\varphi(x)))^{\prime}=f^{\prime}(u) \varphi^{\prime}(x)=f^{\prime}(\varphi(x)) \varphi^{\prime}(x) (f(φ(x)))′=f′(u)φ′(x)=f′(φ(x))φ′(x)
或写为
d y d x = d y d u ⋅ d u d x y x ′ = y u ′ u x ′ \frac{d y}{d x}=\frac{d y}{d u} \cdot \frac{d u}{d x} \quad \quad y_{x}^{\prime}=y_{u}^{\prime} u_{x}^{\prime} dxdy=dudy⋅dxduyx′=yu′ux′
链法则:反映复合过程 y → u → x y \rightarrow u \rightarrow x y→u→x
02 幂指函数的导数
(1) 幂指函数的导数
y = f ( x ) g ( x ) ⇒ y = e g ( x ) ln f ( x ) y=f(x)^{g(x)} \quad \Rightarrow \quad y=e^{g(x) \ln f(x)} y=f(x)g(x)⇒y=eg(x)lnf(x)
(2) 幂指函数求导示例
求 y = x sin x y=x^{\sin x} y=xsinx 的导数
03 对数求导法
(1) 对数求导法
y = f ( x ) g ( x ) ⇒ ln y = g ( x ) ln f ( x ) y=f(x)^{g(x)} \Rightarrow \ln y=g(x) \ln f(x) y=f(x)g(x)⇒lny=g(x)lnf(x)
注意,多因子相乘的函数也可用对数求导法
(2) 对数求导法示例
求 y = sin x 3 x − 2 ( x − 2 ) 2 3 y=\frac{\sin x \sqrt{3 x-2}}{\sqrt[3]{(x-2)^{2}}} y=3(x−2)2sinx3x−2 的导数
问题:初等函数在有定义处都可导吗?
四、导数表
( c ) ′ = 0 ( x α ) ′ = α x α − 1 ( a x ) ′ = a x ln x e x = e x ( log a x ) ′ = 1 x ln a ( ln x ) ′ = 1 x ( sin x ) ′ = cos x ( cos x ) ′ = − sin x ( tan x ) ′ = sec 2 x ( cot x ) ′ = − csc 2 x ( sec x ) ′ = sec x tan x ( csc x ) ′ = − csc x cot x ( arcsin x ) ′ = 1 1 − x 2 , ( arccos x ) ′ = − 1 1 − x 2 ( arctan x ) ′ = 1 1 + x 2 ( arccot x ) ′ = 1 1 + x 2 \begin{aligned} &(c)^{\prime}=0 \quad\left(x^{\alpha}\right)^{\prime}=\alpha x^{\alpha-1} \quad\left(a^{x}\right)^{\prime}=a^{x} \ln x \quad e^{x}=e^{x} \\ &\left(\log _{a} x\right)^{\prime}=\frac{1}{x \ln a} \quad(\ln x)^{\prime}=\frac{1}{x} \\ &(\sin x)^{\prime}=\cos x \quad(\cos x)^{\prime}=-\sin x \\ &(\tan x)^{\prime}=\sec ^{2} x \quad(\cot x)^{\prime}=-\csc ^{2} x \\ &(\sec x)^{\prime}=\sec x \tan x \quad(\csc x)^{\prime}=-\csc x \cot x \\ &(\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}, \quad(\arccos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}} \\ &(\arctan x)^{\prime}=\frac{1}{1+x^{2}} \quad(\operatorname{arccot} x)^{\prime}=\frac{1}{1+x^{2}} \end{aligned} (c)′=0(xα)′=αxα−1(ax)′=axlnxex=ex(logax)′=xlna1(lnx)′=x1(sinx)′=cosx(cosx)′=−sinx(tanx)′=sec2x(cotx)′=−csc2x(secx)′=secxtanx(cscx)′=−cscxcotx(arcsinx)′=1−x21,(arccosx)′=−1−x21(arctanx)′=1+x21(arccotx)′=1+x21
五、微分运算法
01 利用可微与可导的关系导出
d ( u ± v ) = d u ± d v d ( u v ) = v d u + u d v d ( u v ) = v d u − u d v v 2 \begin{aligned} &d(u \pm v)=d u \pm d v \\ &d(u v)=v d u+u d v \\ &d\left(\frac{u}{v}\right)=\frac{v d u-u d v}{v^{2}} \end{aligned} d(u±v)=du±dvd(uv)=vdu+udvd(vu)=v2vdu−udv
02 一阶微分形式不变性
对 y = f ( u ) y=f(u) y=f(u),无论 u u u 是自变量还是函数,总有 d y = f ′ ( u ) d u d y=f^{\prime}(u) d u dy=f′(u)du .
03 微分在近似计算中的应用
(1) 近似计算
Δ f = f ′ ( x ) Δ x + o ( Δ x ) = d f + o ( Δ x ) ⇒ Δ f ≈ d f ⇒ f ( x + Δ x ) ≈ f ( x ) + f ′ ( x ) Δ x \begin{aligned} & \Delta f=f^{\prime}(x) \Delta x+o(\Delta x)=d f+o(\Delta x) \\ \Rightarrow &\quad\quad \Delta f \approx d f \\ \Rightarrow &\ \ f(x+\Delta x) \approx f(x)+f^{\prime}(x) \Delta x \end{aligned} ⇒⇒Δf=f′(x)Δx+o(Δx)=df+o(Δx)Δf≈df f(x+Δx)≈f(x)+f′(x)Δx
(2) 误差问题
若 x x x 为准确值, x 0 x_0 x0 为测量值,有以下概念:
绝 对 误 差 : ∣ Δ x ∣ = ∣ x − x 0 ∣ 相 对 误 差 : ∣ Δ x ∣ ∣ x 0 ∣ 最 大 绝 对 误 差 : ∣ Δ x ∣ 不 超 过 δ 最 大 相 对 误 差 : δ ∣ x 0 ∣ 计 算 式 y = f ( x ) 引 起 的 绝 对 和 相 对 误 差 ∣ Δ y ∣ ≈ ∣ f ′ ( x 0 ) ∣ ⋅ ∣ Δ x ∣ ≤ ∣ f ′ ( x 0 ) ∣ δ \begin{aligned} & 绝对误差: |\Delta x|=\left|x-x_{0}\right|\\ & 相对误差: \frac{|\Delta x|}{|x_0|} \\ & 最大绝对误差: |\Delta x|不超过 \delta\\ & 最大相对误差: \frac{\delta}{|x_0|}\\ & 计算式 y=f(x) 引起的绝对和相对误差\\ & \quad |\Delta y| \approx |f'(x_0)|\cdot|\Delta x|\leq|f'(x_0)|\delta \end{aligned} 绝对误差:∣Δx∣=∣x−x0∣相对误差:∣x0∣∣Δx∣最大绝对误差:∣Δx∣不超过δ最大相对误差:∣x0∣δ计算式y=f(x)引起的绝对和相对误差∣Δy∣≈∣f′(x0)∣⋅∣Δx∣≤∣f′(x0)∣δ
第四节 隐函数求导法
一、隐函数的导数
原则:利用复合函数求导法,分清哪个是自变量、哪个是因变量(函数)?
二、参数方程形式函数的导数
参 数 方 程 形 式 函 数 的 导 数 { x = x ( t ) y = y ( t ) t 为参数 利 用 链 法 则 d y d x = d y d t d x d t 或 y x ′ = y t ′ x t ′ \begin{aligned} & 参数方程形式函数的导数\ \ \left\{\begin{array}{l} x=x(t) \\ y=y(t) \end{array} \quad t\right. \text { 为参数 }\\ & 利用链法则\ \ \frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}} \ \ 或\ \ y_{x}^{\prime}=\frac{y_{t}^{\prime}}{x_{t}^{\prime}} \end{aligned} 参数方程形式函数的导数 {x=x(t)y=y(t)t 为参数 利用链法则 dxdy=dtdxdtdy 或 yx′=xt′yt′
第五节 导数概念在实际问题中的应用
相关变化率问题
圆锥形水池高 H = 10 m H=10 \mathrm{~m} H=10 m,上底面半径 R = 4 m R=4 m R=4m,
以 v = 5 m 3 / m i n v=5 m^{3} / \mathrm{min} v=5m3/min 的速度注水入池,求水深 5 米时池中水面上升的速度。
第六节 高阶导数
一、定义
01 二阶导数
f ( x ) f(x) f(x) 在 x 0 x_{0} x0 的二阶导数
f ′ ′ ( x 0 ) = d e f ( f ′ ( x ) ) ′ ∣ x = x 0 \left.f^{\prime \prime}\left(x_{0}\right) \stackrel{d e f}{=}\left(f^{\prime}(x)\right)^{\prime}\right|_{x=x_{0}} f′′(x0)=def(f′(x))′∣∣∣x=x0
还可以记为
f ′ ′ ∣ x = x 0 或 d 2 f d x 2 ∣ x = x 0 \left.f^{\prime \prime}\right|_{x=x_{0}} \text { 或 }\left.\frac{d^{2} f}{d x^{2}}\right|_{x=x_{0}} f′′∣x=x0 或 dx2d2f∣∣∣∣x=x0
若 f ( x ) f(x) f(x) 在区间 I I I 的每点 x x x 有二阶导数,则称 f ( x ) f(x) f(x) 在 I I I 二阶可导,
f ′ ′ ( x ) f^{\prime \prime}(x) f′′(x) 称为 f ( x ) f(x) f(x) 的二阶导函数 ( 简称二阶导数 ) 。
02 n n n 阶导数
归纳地定义
f ( n ) ( x 0 ) = ( f ( n − 1 ) ( x ) ) ′ ∣ x = x 0 f^{(n)}\left(x_{0}\right)=\left.\left(f^{(n-1)}(x)\right)^{\prime}\right|_{x=x_{0}} f(n)(x0)=(f(n−1)(x))′∣∣∣∣x=x0
称为 f ( x ) f(x) f(x) 在 x 0 x_{0} x0 的 n n n 阶导数,可记为
f ( n ) ∣ x = x 0 或 d n f d x n ∣ x = x 0 \left.f^{(n)}\right|_{x=x_{0}} \text { 或 }\left.\frac{d^{n} f}{d x^{n}}\right|_{x=x_{0}} f(n)∣∣∣x=x0 或 dxndnf∣∣∣∣x=x0
若 f ( x ) f(x) f(x) 在区间 I I I 的每点 x x x 有 n n n 阶导数,则称 f ( x ) f(x) f(x) 在 I I I 上 n n n 阶可导,
f ( n ) ( x ) f^{(n)}(x) f(n)(x) 为 f ( x ) f(x) f(x) 的 n n n 阶导函数。若 f ( n ) ( x ) f^{(n)}(x) f(n)(x) 在区间 I I I 连续,记为 f ( x ) ∈ C n ( I ) f(x) \in C^{n}(I) f(x)∈Cn(I) 。
二、运算法则
01 主要法则
( u ± v ) ( n ) = u ( n ) ± v ( n ) ( c u ) ( n ) = c u ( n ) ( u v ) ( n ) = u ( n ) v + C n 1 u ( n − 1 ) v ′ + ⋯ + C n n − 1 u ′ v ( n − 1 ) + u v ( n ) ( 莱 布 尼 兹 法 则 ) \begin{aligned} &\ (u \pm v)^{(n)}=u^{(n)} \pm v^{(n)} \\ &\ (c u)^{(n)}=c u^{(n)} \\ &\ (u v)^{(n)}=u^{(n)} v+C_{n}^{1} u^{(n-1)} v^{\prime}+\cdots+C_{n}^{n-1} u^{\prime} v^{(n-1)}+u v^{(n)} \\ &\quad\quad\quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad (莱布尼兹法则) \end{aligned} (u±v)(n)=u(n)±v(n) (cu)(n)=cu(n) (uv)(n)=u(n)v+Cn1u(n−1)v′+⋯+Cnn−1u′v(n−1)+uv(n)(莱布尼兹法则)
02 隐函数的高阶导数
( 1 ) 求 由 e y + x y = e 所 确 定 的 隐 函 数 y = y ( x ) 在 x = 0 处 的 二 阶 导 数 ( 2 ) { x = a cos t y = b sin t 求 二 阶 导 数 d 2 y d x 2 ( 3 ) y = arcsin x , 求 y ( n ) ( 0 ) ( 4 ) 将 方 程 d 2 y d x 2 − x 1 − x 2 d y d x + y 1 − x = 0 由 变 换 x = cos t 化 为 y 关 于 t 的 方 程 。 \begin{aligned} & (1)\ \ 求由 e^{y}+x y=e 所确定的隐函数 y=y(x) 在 x=0 处的二阶导数\\ & (2)\ \ \left\{\begin{array}{l}x=a \cos t \\ y=b \sin t\end{array}\right. \ \ 求二阶导数 \frac{d^{2} y}{d x^{2}}\\ & (3)\ \ y=\arcsin x, 求 y^{(n)}(0)\\ & (4)\ \ 将方程\ \frac{d^{2} y}{d x^{2}}-\frac{x}{1-x^{2}} \frac{d y}{d x}+\frac{y}{1-x}=0 \ 由变换\ x=\cos t \ 化为\ y\ 关于\ t\ 的方程。 \end{aligned} (1) 求由ey+xy=e所确定的隐函数y=y(x)在x=0处的二阶导数(2) {x=acosty=bsint 求二阶导数dx2d2y(3) y=arcsinx,求y(n)(0)(4) 将方程 dx2d2y−1−x2xdxdy+1−xy=0 由变换 x=cost 化为 y 关于 t 的方程。