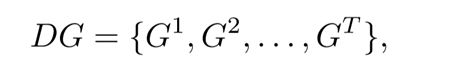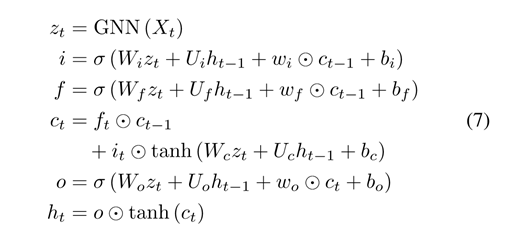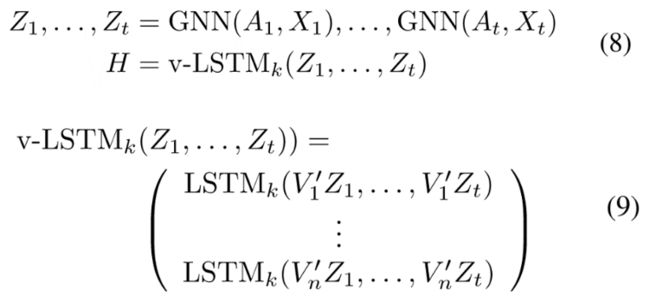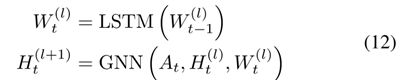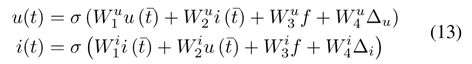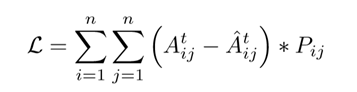论文导读 | 动态图上神经网络模型综述
![]()
北京大学 李荆
编者按:
原文《Foundations and modelling of dynamic networks using Dynamic Graph Neural Networks: A survey》介绍一篇关于动态图上的神经网络模型的综述,本篇综述的主要结构是根据动态图上进行表示学习过程的几个阶段(动态图表示、模型学习、模型预测)进行分别阐述。包括
1. 系统的探讨不同维度下的动态图分类方法以及各种方法下的数据表示格式
2. 针对不同类别的动态图归纳目前图表示学习的主流算法模型(encoding部分)
3. 分别讨论在预测阶段的主要方法,包括decoding, loss function, evaluation metrics等。
![]()
01
Dynamic networks
动态图的定义可以看作一个节点和边随着时间不断变化的图结构。在动态图的表示中,一个节点包括节点本身以及它生存的起始时间和结束时间,一条边也有端点u,v以及这条边的起始时间和结束时间。
目前关于图表示学习的研究中有很多的工作都聚焦在这种节点和边随时间变化的图结构上,但是在不同的论文中,所用的名词各有不同,比如dynamic networks, temporal networks, evolutionary networks, time-varying networks等等。为了对动态图有一个更加全面,规范的认识,首先探讨对于动态图的分类方法。
A. temporal granularity.
从对于动态性的粒度上来划分,我们可以将动态图划分为四类,static,edge weighted,discrete,continuous,他们的模型复杂程度依次增强,对于动态性的关注也依次增强。
对于static的网络,我们不关注图中的动态性信息,而将其作为一张静态图同等处理。
对于edge weighted networks,我们虽然也关注动态性,但图中的动态信息只是作为一张静态图中的节点或者边的labels而存在。
第三类离散型的动态图,是指以离散的时间片对图进行划分表示,动态图被看作不同时间段之间的多个静态图的集合。
这种表示的优点是能够有效的利用到目前静态图上的方法,分别对每个snapshot进行建模,之后再综合考虑不同snapshot之间的动态性。
第四类,连续型的动态图,它将图的变化看作不断发生的事件,是对动态性保留最多的,但同时也是最复杂的一类。举例来说有以下几种:
The event-based representation:
每个边包含了该事件的起始时间和持续时间。
The contact sequence representation:
是event-based的表示方法的一种特例和简化,当某些事件是瞬时发生的,或者说它们的持续时间不重要,比如邮件发送网络等,此时我们可以省略掉事件的持续时间表示。
The graph stream representation:
在这种表示中将边的产生和消失分别看作不同的事件,用第四位的-1(删除边)和1(插入边)的标志位表示。
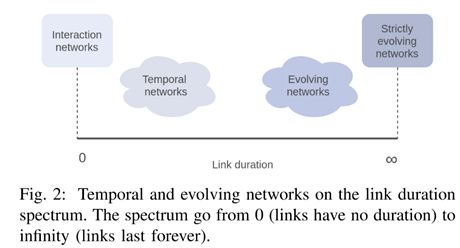
B. link duration
根据边的持续时间长短可以分为四类:
temporal networks:边有一定的持续时间,但也较短,在任何时刻都非平凡,因此不能直接将静态图的性质运用到此类网络。
evolving networks:边的持续时间比较长,足够能在此时间段内建立一个稳定的网络结构,因此可以将静态图的性质运用到此类图上,并随着网络结构的变化而不断更新。在这类图中,边的产生和消失被看作两种事件。
极端情况:
interaction networks:当边的持续时间为零的情况,也即事件是瞬时的。
strictly evolving networks:严格增长的网络,边的持续时间为正无穷,边一旦插入就会一直存在。
比如邮件网络可以看作interaction network,而引文网络则可以看作一个strictly evolving network,当然,对于这些场景下的网络类别并不是一成不变的,对于不同的应用场景,关注重点不同的情况,也会产生转变。
C. node dynamics
static:当动态图中节点集不变,只是节点之间的连边产生变化时,我们称之为node static的
dynamic: 表示图中的节点也会新增或消失。
Growing:图中的节点只会不断新增(node dynamic的一种特例)
上述的多种维度的分类方法可以任意组合,由此产生多种不同类型的动态图,例如下图所示,node static temporal network或者node nynamic evolving network等等
如果把分类的三个维度作为坐标轴的三个维度,我们可以得到下图的一个动态图立方体,在这个立方体的各个角都表示一种不同类别的动态图
02
Dynamic graph neural networks
动态图的模型有多种,比如基于随机游走,基于矩阵分解等等,而本文的分析主要是集中在动态图上的神经网络模型上。
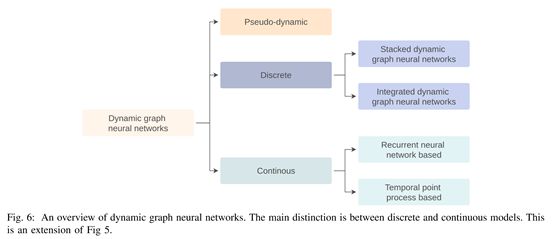
A. discrete dynamic graph neural networks
其中GNN用来encode每个snapshot,而函数f(可以是RNN或者是self-attention)则用来encode不同snapshots之间的时序关系。
a) stacked dynamic graph neural networks:
通过不同的GNN在不同的snapshot上单独进行空间信息聚合,之后将不同时间片的GNN输出作为时序模块(如RNN)的输入,进行序列建模。
i. GCRN-M1 [Seo et al.] :
将spectral GCN [Michael et al.] 与peephole LSTM [Felix et al.]相结合。
其中 i, f, o分别为输入门,遗忘门,输出门,而peephole LSTM在标准LSTM基础上加上peephole connection,即将前一时刻长期记忆ct-1也作为遗忘门和输出门控制器的一个输入,当前时刻长期记忆ct也作为输出门控制器的一个输入。此类方法的做法基本与此类似,只是不同的架构选择的GNN或者RNN会有区别,比如用spatial GCN 或者用standard LSTM等等。
ii. WD-GCN
CD-GCN [Manessi et al.]:将GCN [Kipf and Welling] 与LSTM相结合,同时,对于每个节点,会有一个LSTM(虽然这些LSTM之间共享权重),两个模型的区别在于CD-GCN在GCN上加入了skip-connection。
b) Integrated dynamic graph neural networks:
将GNN和RNN集成到同一层网络层中,因此可以将空间建模和时间建模集成到同一个网络层。
i. GCRN-M2
用graph convolution替换传统的convolution操作。
ii. EvolveGCN
与前面不同的是,EvolveGCN用RNN来更新不同snapshot的GCN的权重参数,而不是用RNN来更新节点表示向量。
该模型提出了两个变种,EGCU-O使用GRU进行GCN权重参数更新,而EGCU-H是用LSTM进行更新。
EGCU-H:
EGCU-O:
c) dynamic graph autoencoders and generative models:
i. DynGEM [palash et al.]:
用autoencoder对每个snapshot进行encoding,同时,当前时刻的autoencoder的参数用前一时刻的参数进行初始化,这加速了训练的收敛过程,同时让不同时刻间的embeddings的变化相对稳定。
ii. DynGraph2vec [palash et al.]:
在DynGEM的基础上进行改进,不再是只考虑前一个时刻对当前状态的影响,而是考虑前l时刻,也即维护一个滑动窗口。用t, t+1, …,t+l时刻的邻接表来预测t+l+1时刻的邻接表。该工作包括三个变体,dyngraph2vecAE,dyngraph2vecRNN, dyngraph2vecAERNN,它们的区别在于encoder和decoder的选择不同上。
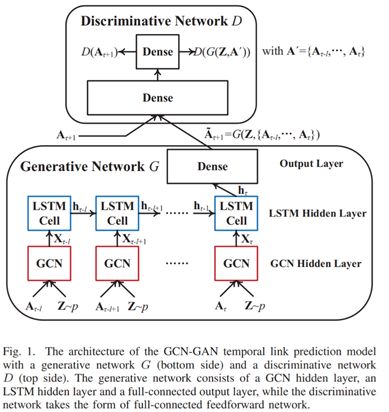
iii. GCN-GAN [Kai et al.] and DyngraphGAN [Yun et al.]:
通过GAN的架构优化embedding的学习过程。Generator用来生成邻接矩阵,而discriminator区分邻接矩阵是产生的还是真实的。在这个过程中generator尽可能的让discriminator无法分辨,而discriminator则不断训练去正确分辨,在这样的min-max博弈过程中,优化中间的embedding表示。
B. continuous dynamic graph neural networks:
a) RNN based models:
用RNN来实时的更新节点embedding,一旦某时间发生,即更新所有受影响的节点的embedding。保证节点表示能够得到及时更新且连续。
i. Streaming graph neural networks [Yao et al.]
由两个结构组成,分别是update组件和propagation组件。Update部分负责在某事件发生后更新事件关联的两个节点的表示。而propagation组件负责在变化发生后将网络变化传播到相邻节点(比如新增边的端点的一跳邻居)。
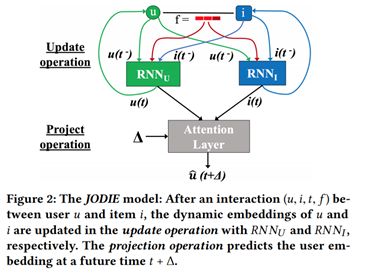
ii. JODIE [srijan et al]:
此模型关注于interaction network,用于建模推荐系统中的user-item网络,RNN结构用来分别更新User和item的表示。当一个交易产生,那么分别实时更新User和item,更新方式如下:
b) Temporal point process based models
i. DyRep [Rakshit et al.] :
将网络的动态性理解为两种动态性:dynamics of the network(即网络拓扑结构的变化)和 dynamics on the network(即网络中节点之间的交互作用)。其中dynamics of the network可以看作网络的association process, 而dynamics on the network则看作网络的communicaiton process。而动态图的节点表示学习则是这样两个过程的中间媒介。Association->embedding->communication, communication->embedding->association,网络拓扑结构的变化,带来embedding的变化,而这种变化引起网络中节点的communication,进一步又会带来与之相关节点embedding的变化,从而因此网络结构的变化这样一个循环过程。
总结来说,这些方法的优势和特定如下表:
03
Prediction of network topology (link prediction)
Time-predicting: 预测一个事件何时会发生(when),time-conditioned:预测一个事件在t时刻是否会发生。
A. decoders:
一种是通过前s个时刻的embedding预测t时刻,一种是通过上一个时刻预测t时刻,比如kipf and Welling通过将两个节点的embedding的Inner product来预测两点之间是否有边。而DyRep则是通过建模事件发生的条件概率密度的大小来预测事件是否发生,对于一个事件p=(u, v, t, k), u, v 点之间的条件概率密度大小定义为:
B. loss function
i. 链接预测:将链接预测看作一个二分类问题,loss function通常采用二分类的交叉熵,有时候也会采用负采样的做法。
ii. autoencoder方法:重建邻接矩阵的误差最小化作为训练的损失函数,通常也会加入额外的正则项
iii. temporal point process:DyRep通过建模点过程来优化学习过程,在引入事件发生概率密度基础上,损失函数让有边相连的节点间概率密度最大,而无边相连的最小。
![]()
C. evalution metrics
i. area under the curve (AUC):评价一个二分类模型,且与阈值无关,AUC即为ROC曲线之下的面积,而ROC曲线是true positive rate和false positive rate之间的曲线关系。
ii. PRAUC:指precision recall曲线下的面积,通常用在信息检索领域中类别分布不均衡的场景下。
iii. Fixed-threshold metrics:precision@k=kr/k, 表示在top k的预测中有kr个预测正确。但此评价指标依赖于k的选择,不同阈值会对结果产生影响,因此一般用在有确定分类阈值的任务中,比如推荐系统等。
iv. Mean average precision (MAP):MAP是average precision(AP)值的平均,计算方式为:
v. Sum of absolute differences (SumD):衡量了被误分类的链接数,false positive的影响较大,因为有大量的边是未出现的,所以一个微小的False positive升高,都会带来结果的极大变化。
vi. Error rate:根据所有存在的链接数量对SumD做了normalize后的结果。
vii. GMAUC:将动态图链接预测看作两个子问题:1. 预测已经存在的边的消失,或者曾经存在的边再次出现。(AUC)2. 预测那些之前从未存在过的边。(PRAUC)。区分并综合考量了新产生的边和之前曾经存在过的边,而不会因为其中一种类型对结果产生影响。
总结
本文从动态图的分类,不同类别动态图上的模型架构,以及将上述模型用于后续预测任务所需考虑的不同decoder,loss function,evaluation metric等等方面,详细的阐述了动态图神经网络设定下的一系列问题。对于后续关于动态图方面的表示学习工作有很强的参考意义和启发价值。
![]()
更多链接
论文导读 | Truss decomposition并行算法
论文导读 | 图数据流子图查询
讲座录播|图数据管理与分析在线名家讲座-第七期
图谱动态|学苑周刊 NO.28
图谱动态|学苑周刊 NO.27
![]()
![]()