基于深度学习的点云配准Benchmark
文章和代码已更新:
- 最新版本的文章: https://zhuanlan.zhihu.com/p/289620126
- 最新版本的代码: https://github.com/zhulf0804/PCReg.PyTorch
1. 概要
最近几年,基于深度学习的点云配准算法不断被提出,包括PointNetLK[1],Deep ICP[2],DCP[3],PRNet[4],IDAM[5],RPM-Net[6],3DRegNet[7],DGR[8]等。这些网络在ModelNet40,Kitti,或3DMatch数据集上进行试验,其性能与速度均超过了传统的ICP算法。这些算法或者网络结构较为复杂,或者结果难以复现,对于把深度学习应用到点云配准的初学者而言,不是很友好。这里结合自己的感触和最近阅读的PCRNet[9] (两者不谋而合),介绍一种非常简单的点云配准网络,或许它的结果不如前面提到的DCP, 3DRegNet等效果好,但其简洁易懂,且效果在ModelNet40上仍优于ICP,速度快于ICP。
本文将要介绍的网络是基于PointNet + Concat + FC的,它没有其它复杂的结构,易于复现。因其简洁性,这里暂且把其称作点云配准的Benchmark。因作者源码中复杂的(四元数, 旋转矩阵, 欧拉角之间)的变换操作和冗余性,且其PyTorch版本的不完整性(缺少评估模型等,最近又更新了),于是根据自己的理解,从头撸了一遍整个模型: 数据,网络,评估,训练,测试,可视化等操作,代码已开源https://github.com/zhulf0804/PCReg.PyTorch。
章节2介绍模型的Dataloader部分,就是怎么组织数据的; 章节3介绍模型的网络部分; 章节4介绍损失函数; 章节5介绍评估指标; 章节6介绍模型的实现及实现过程中遇到的一些坑; 章节7介绍本库的一些实验结果; 章节8介绍一些补充信息,如四元数、旋转矩阵和欧拉角之间的关系等。
2. 数据
实验的数据为不带有normal信息的ModelNet40,下载地址为modelnet40_ply_hdf5_2048.zip。训练集中包括9840个样本,测试集中包括2468个样本,每个样本均包括2048个数据点。
-
训练
对训练集中的每个样本template,随机选择1024个点,并随机产生一个旋转矩阵R和平移向量t,其中R是绕z轴旋转 θ 1 ∈ [ − π 4 , π 4 ] \theta_1 \in [-\frac{\pi}{4}, \frac{\pi}{4}] θ1∈[−4π,4π],绕y轴旋转 θ 2 ∈ [ − π 4 , π 4 ] \theta_2 \in [-\frac{\pi}{4}, \frac{\pi}{4}] θ2∈[−4π,4π],绕z轴旋转 θ 3 ∈ [ − π 4 , π 4 ] \theta_3 \in [-\frac{\pi}{4}, \frac{\pi}{4}] θ3∈[−4π,4π]随机生成,t是从[-1, 1]均匀采样生成。把R, t作用于template点云,生成source点云,这样就得到待配准的点云对。
在训练时,需要做噪声数据增强,对source点云和template点云中的每个点(x, y, z)加上随机高斯噪声。
-
测试
对测试集中的每个样本template,选择全部的2048个点,同时产生一个旋转矩阵R和平移向量t(产生方式同训练),把R, t作用于template点云,生成source点云,这样就得到了待配准的点云对。
为了公平的对比不同的方法,需要设置随机种子,保证每次测试随机产生的R,t都一样。
-
相关代码在
./data/ModelNet40.py.
3. 网络
-
Benchmark
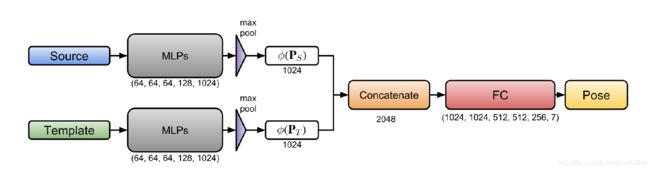
Benchmark网络架构如上图所示,它的输入包括source点云和template点云,输出是一个7维向量,表示平移向量 t ∈ R 3 t \in \mathbb R^3 t∈R3和单位四元数 q ∈ R 4 q \in \mathbb R^4 q∈R4(q是单位向量)。
Benchmark把点云配准当做回归问题,它包括提取特征层和回归层。提取特征层是一个PointNet类的网络,对点云 P S P_S PS和 P T P_T PT中的每一个点进行1D卷积Conv1d(3, 64, 64, 128, 1024),这样对每个点生成了1024维的特征,接下来进行MaxPooling操作,source点云 P S P_S PS和template点云 P T P_T PT分别得到了1024维的特征 ϕ ( P S ) \phi(P_S) ϕ(PS)和 ϕ ( P T ) \phi(P_T) ϕ(PT)。 P S P_S PS和 P T P_T PT经过的特征提取层是参数共享的。
为了预测source点云和template点云之间的变换,需要在两者之间建立联系,这里采用了Concat操作。两个点云的特征通过Concat操作变成了2048维的特征。接下来的回归层就是全连接层FC(2048, 1024, 1024, 512, 512, 256, 7)。
网络的输出就是平移向量和四元数,四元数进一步可以转化成旋转矩阵(变换公式参考章节8中的补充信息)。
-
Iterative Benchmark
Benchmark网络结构比较简单,相信很多人可以设计出这样的网络,但经过试验发现,这样的网络效果较差,在ModelNet40上仍旧不能很好的配准。因此在Benchmark的基础上,提出了下面的Iterative Benchmark。
Iterative Benchmark包括n个Benchmark(PCRNet),要注意的是这n个Benchmark的权重是共享的,因此网络的容量是没有增加的,和Benchmark的参数一样。Iterative Benchmark是如何工作的呢?
在第一次迭代中,source点云和template点云被送入到Benchmark(PCRNet),得到初始的变换T(1)。在下一次迭代中,T(1)作用于source点云得到transformed点云,和原始的template点云一块送入到Benchmark(PCRNet)。经过n次迭代,原始的source点云和template点云之间的变换为每一次迭代变换的组合:
T = T ( n ) × T ( n − 1 ) . . . × T ( 1 ) T = T(n) \times T(n-1) ... \times T(1) T=T(n)×T(n−1)...×T(1)
-
相关代码在
./models/benchmark.py
4. 损失函数
应用于点云配准中的Loss比较多,关于R, t的MSE Loss,关于欧拉角的Loss,关于点云的CD(Chamfer Distance) Loss和EMD(Earth Mover) Loss。
本模型中采用的EMD Loss(最先实验了CD Loss,效果不理想),实现的代码是借鉴于网上的开源库https://github.com/meder411/PyTorch-EMDLoss。
-
EMD(Earth Mover Distance) Loss
E M D ( P S est , P T ) = min ψ : P S est − > P T 1 ∣ P S est ∣ Σ x ∈ P S est ∣ ∣ x − ψ ( x ) ∣ ∣ 2 EMD(P_S^{\text{est}}, P_T) = \min_{\psi: P_S^{\text{est}} -> P_T} \frac{1}{|P_S^{\text{est}}|}\Sigma_{x \in P_S^{\text{est}}}||x - \psi(x)||_2 EMD(PSest,PT)=ψ:PSest−>PTmin∣PSest∣1Σx∈PSest∣∣x−ψ(x)∣∣2
-
CD(Chamfer Distance) Loss
C D ( P S est , P T ) = Σ x ∈ P S est min y ∈ P T ∣ ∣ x − y ∣ ∣ 2 + Σ y ∈ P T min x ∈ P S est ∣ ∣ x − y ∣ ∣ 2 CD(P_S^{\text{est}}, P_T) = \Sigma_{x \in P_S^{\text{est}}} \min_{y \in P_T}||x - y||_2 + \Sigma_{y \in P_T } \min_{x \in P_S^{\text{est}}}||x-y||_2 CD(PSest,PT)=Σx∈PSesty∈PTmin∣∣x−y∣∣2+Σy∈PTx∈PSestmin∣∣x−y∣∣2
本库的loss代码在 ./loss/earth_mover_distance.py.
5. 评估指标
评估指标主要4个: mse_R, mse_t, mse_degree, time。前面3个和精度有关系,time是和效率有关。
-
mse_R
mse _ R = Σ i = 1 N ∣ ∣ R pred i − R gt i ∣ ∣ 2 \text{mse}\_R = \Sigma_{i=1}^N||R_{\text{pred}}^i - R_{\text{gt}}^i||_2 mse_R=Σi=1N∣∣Rpredi−Rgti∣∣2
N表示待配准点云对的数量。
-
mse_t
mse _ t = Σ i = 1 N ∣ ∣ t pred i − t gt i ∣ ∣ 2 \text{mse}\_t = \Sigma_{i=1}^N||t_{\text{pred}}^i - t_{\text{gt}}^i||_2 mse_t=Σi=1N∣∣tpredi−tgti∣∣2
-
mse_degree
mse _ degree = Σ i = 1 N ∣ ∣ θ pred i − θ gt i ∣ ∣ 2 \text{mse}\_\text{degree} = \Sigma_{i=1}^N||\theta_{\text{pred}}^i - \theta_{\text{gt}}^i||_2 mse_degree=Σi=1N∣∣θpredi−θgti∣∣2
θ \theta θ表示欧拉角。
-
time
每个点云对配准的平均时间。
-
相关代码在
./metrics/metrics.py
6. 实现
网络结构虽然简单,但使其能有效work还是很困难的,先说一下在实现过程中走过的坑:
- 网络结构: 加bn层会使网络的结果变差。
- 迭代: 基于Benchmark训练的网络效果远不如Iterative Benchmark的结果。
- 损失函数: CD Loss训练的结果不如EMD Loss。
- 优化器很: EMD Loss在SGD优化器下出现nan,一种有效的策略是采用Adam优化器训练EMD Loss。
- 初始学习率: 初始学习率设置为1e-2,出现梯度爆炸,最终收敛的值较大; 初始学习率设置为1e-5,收敛时的权重在评估指标上仍然不好。
- 在训练和预测时,减点云的均值是不合理的(原作者的代码是这么实现的),因为会使得点云的平移尺度接近于0.
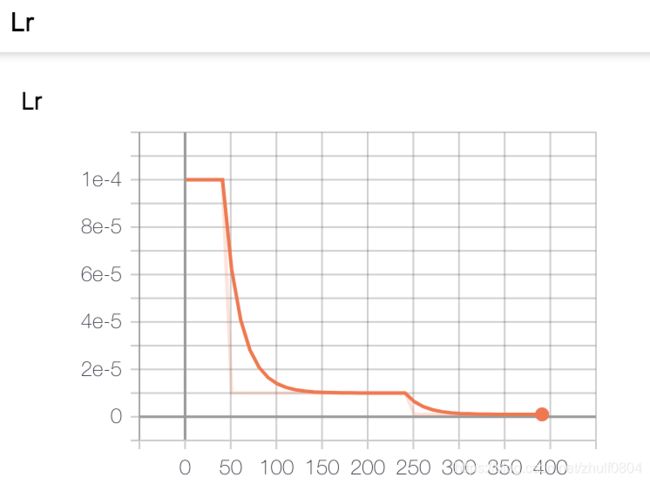
因此,最终在实现时,采用了Iterative Benchmark模型、EMD Loss、Adam优化器。batchsize设置为16,训练400 epoches,初始学习率设置为1e-4,学习率下降采用MultiStepLR[50, 250]。在训练和预测时均不减点云的均值。
另外,要注意的是,一个batchsize中不同的组织数据会带来网络训练的不稳定性,比如相同的代码,不改任何配置,由于shuffle的存在,训练结果差别挺大的;因此在训练时设置了随机种子,保证训练结果的可复现性。
7. 实验结果
7.1 实验结果
实验比较了Iterative Benchmark和ICP在ModelNet40测试集上的精度和时间,实验结果如下表:
| Method | mse_t | mse_R | mse_degree | time(s) |
|---|---|---|---|---|
| icp | 0.40 | 0.38 | 11.86 | 0.06 |
| Iterative Benchmark | 0.35 | 0.18 | 7.90 | 0.02 |
从表中可以看到,Iterative Benchmark在ModelNet40测试集上的配准结果,从精度(mse_t, mse_R, mse_degree)和速度(time)上是优于ICP的。
7.2 实验结果可视化
-
ICP与Iterative Benchmark的对比
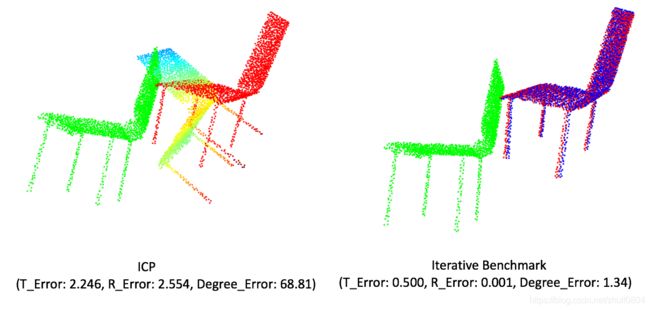
左图是ICP的配准结果,右图是Iterative Benchmark的配准结果。图中的绿色点云表示source点云,红色点云表示template点云,另外一个颜色的点云表示transformed source点云,即把source点云与template点云配准得到R,t,然后R,t作用于source点云后的结果。括号内表示是平移t的误差,旋转矩阵R的MSE误差和旋转角度degree的误差。
从可视化结果可以看到,当待配准点云的初始位置不好时,Iterative Benchmark的配准结果优于ICP的配准结果。
-
Iterative Benchmark的bad cases
上图是一个bad case,当具有重复性结构时,Iterative Benchmark的结果是不理想的,其结果弱于ICP算法。
7.3 训练过程可视化
7.4 思考
Iterative Benchmark在ModelNet40数据集的大部分cases的配准结果比较好的,但以下问题还需要解决:
- 重复性结构或者复杂结构点云的配准
- 真实数据点云的配准
- 部分-部分点云的配准
8. 补充
本章节介绍一些三维旋转的内容,参考了https://en.wikipedia.org/wiki/Rotation_matrix#Axis_of_a_rotation和https://zhuanlan.zhihu.com/p/45404840。
-
四元数转旋转矩阵
设单位四元数 q = w + x i + y j + z k \mathbf{q} = w + x\mathbf i + y \mathbf j + z \mathbf k q=w+xi+yj+zk,其旋转矩阵为:
R ( q ) = [ 1 − 2 y 2 − 2 z 2 2 x y − 2 z w 2 x z + 2 y w 2 x y + 2 z w 1 − 2 x 2 − 2 z 2 2 y z − 2 x w 2 x z − 2 y w 2 y z + 2 x w 1 − 2 x 2 − 2 y 2 ] R(q) = \left[ \begin{matrix} 1 - 2y^2 - 2z^2 & 2xy - 2zw & 2xz + 2yw \\ 2xy + 2zw & 1 - 2x^2 - 2z^2 & 2yz - 2xw \\ 2xz - 2yw & 2yz + 2xw & 1 - 2x^2 - 2y^2 \end{matrix} \right] R(q)=⎣⎡1−2y2−2z22xy+2zw2xz−2yw2xy−2zw1−2x2−2z22yz+2xw2xz+2yw2yz−2xw1−2x2−2y2⎦⎤
-
旋转矩阵转四元数
w = t r ( R ) + 1 2 w = \frac{\sqrt{tr(R) + 1}}{2} w=2tr(R)+1
x = R 32 − R 23 4 w x = \frac{R_{32} - R_{23}}{4w} x=4wR32−R23
y = R 13 − R 31 4 w y = \frac{R_{13} - R_{31}}{4w} y=4wR13−R31
z = R 21 − R 12 4 w z = \frac{R_{21} - R_{12}}{4w} z=4wR21−R12
-
旋转矩阵转欧拉角
∣ θ ∣ = arccos ( T r ( R ) − 1 2 ) |\theta| = \arccos(\frac{Tr(R) - 1}{2}) ∣θ∣=arccos(2Tr(R)−1)
T r ( R ) Tr(R) Tr(R)表示矩阵的迹
-
绕x轴旋转矩阵
R x ( θ ) = [ 1 0 0 0 cos θ − sin θ 0 sin θ cos θ ] R_x(\theta) = \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{matrix} \right] Rx(θ)=⎣⎡1000cosθsinθ0−sinθcosθ⎦⎤
-
绕y轴旋转矩阵
R y ( θ ) = [ cos θ 0 sin θ 0 1 0 − sin θ 0 cos θ ] R_y(\theta) = \left[ \begin{matrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos\theta \end{matrix} \right] Ry(θ)=⎣⎡cosθ0−sinθ010sinθ0cosθ⎦⎤
-
绕z轴旋转矩阵
R z ( θ ) = [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] R_{z}(\theta) = \left[ \begin{matrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] Rz(θ)=⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤
-
相关代码在
./utils/process.py
参考资料
[1]. PointNetLK: Point Cloud Registration using PointNet [CVPR 2019]
[2]. DeepICP: An End-to-End Deep Neural Network for 3D Point Cloud Registration [ICCV 2019]
[3]. Deep Closest Point: Learning Representations for Point Cloud Registration [ICCV 2019]
[4]. PRNet: Self-Supervised Learning for Partial-to-Partial Registration [NeurIPS 2019]
[5]. Iterative Distance-Aware Similarity Matrix Convolution with Mutual-Supervised Point Elimination for Efficient Point Cloud Registration [ECCV 2020]
[6]. RPM-Net: Robust Point Matching using Learned Features [CVPR 2020]
[7]. 3DRegNet: A Deep Neural Network for 3D Point Registration [CVPR 2020]
[8]. Deep Global Registration [CVPR 2020]
[9]. PCRNet: Point Cloud Registration Network using PointNet Encoding [arXiv 2019]