KDD 2017 | metapath2vec:异质图的可扩展表示学习
目录
- 前言
- 1. 问题定义
- 2. metapath2vec
-
- 2.1 异质skip-gram
- 2.2 元路径随机游走
- 3. metapath2vec++
- 4. 实验
- 5. 小结
前言

题目: metapath2vec: Scalable Representation Learning for Heterogeneous Networks
会议: KDD 2017
论文地址:metapath2vec: Scalable Representation Learning for Heterogeneous Networks
前面讲了很多图嵌入方法:
- KDD 2016 | node2vec:Scalable Feature Learning for Networks
- KDD 2014 | DeepWalk: 社会表征的在线学习
- WWW 2015 | LINE:大规模信息网络的嵌入
- KDD 2016 | SDNE:结构化深层网络嵌入
- 深入理解拉普拉斯特征映射
后面也讲了不少GNN的知识,GNN也可以作为一种图嵌入的手段:
- ICLR 2017 | GCN:基于图卷积网络的半监督分类
- NeurIPS 2017 | GraphSAGE:大型图的归纳表示学习
- ICLR 2018 | GAT:图注意力网络
- NeurIPS 2016 | VGAE:变分图自编码器
上面所有图嵌入方法都是针对同质图而言的,也就是图中节点和边的类型都只有一种。而在异质图中,节点和边的类型可能有多种,比如基于社区的问答(cQA)站点:用户可以在互联网上发布问题,其他人可以回答问题,那么在cQA图中就有了不同类型的节点:问题、答案、用户,节点间的链接类型也不一样。
metapath2vec与之前的图嵌入方法不同,metapath2vec是专门处理异质图的,利用metapath2vec我们可以得到异质图中多种不同类型节点的潜在向量表示。
1. 问题定义
首先是异质网络的定义: G = ( V , E , T ) G=(V,E,T) G=(V,E,T),图中每个节点 v v v和每条边 e e e都有对应的映射函数 ϕ ( v ) : V → T V \phi(v):V \to T_V ϕ(v):V→TV以及 ϕ ( e ) : E → T E \phi(e):E\to T_E ϕ(e):E→TE, T V T_V TV和 T E T_E TE分别表示节点和边类型的集合,两个集合满足: ∣ T V ∣ + ∣ T E ∣ > 2 |T_V|+|T_E|>2 ∣TV∣+∣TE∣>2,也就是说节点类型数和边类型数之和大于2,即不止一种节点或者一种边。
有了以上定义后,可以将异质图表示学习定义为:给定一个异质图 G G G,其任务是学习到所有节点的嵌入表示 X ∈ R ∣ V ∣ × d X\in R^{|V|\times d} X∈R∣V∣×d,其中 d < < ∣ V ∣ d << |V| d<<∣V∣,嵌入表示 X X X能够捕捉到不同类型节点的结构和语义关系。
值得注意的是,虽然异质图中存在不同类型的节点,但它们都会被映射到相同的空间,也就是说不同类型的节点的表示向量的维度都为 d d d。图嵌入前提是保持节点与其邻域(上下文)之间的邻近性,在异质环境中,异质图嵌入模型的核心是定义和建模“节点-邻居”的概念以及优化嵌入模型,以有效地维护多种类型节点和关系的结构和语义。
2. metapath2vec
2.1 异质skip-gram
论文首先回忆了word2vec模型及其在同质图中的应用。前面提到的DeepWalk和node2vec模型都是基于skip-gram模型,具体来讲是先得到节点的游走序列,然后再将序列输入到skip-gram中以得到每个节点的嵌入表示。
通常,给定一个网络 G = ( V , E ) G = (V, E) G=(V,E),其目标是使网络的局部结构概率最大化,即:

这里 N ( v ) N(v) N(v)指节点 v v v的上下文节点,这种节点的定义方式有多种,比如DeepWalk中利用随机游走得到上下文节点。 p ( c ∣ v ; θ ) p(c|v;\theta) p(c∣v;θ)指已知节点 v v v的情况下,上下文节点 c c c存在的概率,这种概率通常用内积+softmax来实现。
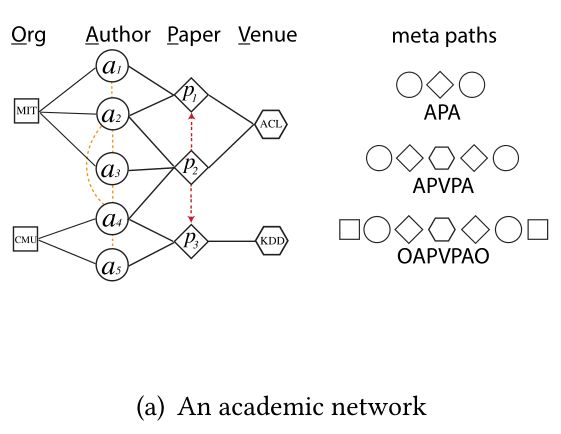
为了将异质网络结构引入到skip-gram,metapath2vec提出了异质skip-gram的概念,即在给定节点 v v v的情况下,最大化其异质上下文节点 N t ( v ) N_t(v) Nt(v)出现的概率:
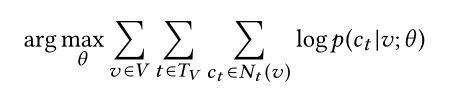
这里 N t ( v ) N_t(v) Nt(v)表示节点 v v v的第 t t t种上下文节点, p ( c t ∣ v ; θ ) p(c_t|v;\theta) p(ct∣v;θ)表示已知节点 v v v的情况下,上下文节点 c t c_t ct存在的概率,一般来讲,这种概率通常用内积+softmax来实现:
p ( c t ∣ v ; θ ) = e X c t ⋅ X v ∑ u ∈ V e X u ⋅ X v p(c_t|v;\theta)=\frac{e^{X_{c_t}\cdot X_v}}{\sum_{u \in V}e^{X_{u}\cdot X_v}} p(ct∣v;θ)=∑u∈VeXu⋅XveXct⋅Xv
与skip-gram中一致,为了解决每次更新时都要对所有节点进行softmax计算的问题,metapath2vec也引入了负采样策略。给定负样本数 M M M,则优化目标可以表示为:

其中 p ( u ) p(u) p(u)是负采样中样本的预定义分布,这个更新公式与带负采样的skip-gram公式基本一致。
2.2 元路径随机游走
同DeepWalk和node2vec等类似,metapath2vec也需要得到节点的游走序列,然后使用2.1中的异质skip-gram模型进行优化。为了得到有效的游走序列,metapath2vec提出了Meta-Path-Based Random Walks,即元路径随机游走。
最简单的一种想法是和DeepWalk一致,进行随机游走,这样也能得到包含不同类型节点的随机游走序列。然而,一些研究表明,异质随机游走偏向于高度可见的节点类型,即那些占据主导地位的路径数量的节点和集中的节点。基于这种理念,本文提出了一种基于元路径的随机游走。
具体来讲,一个meta-path的scheme被定义为:
V 1 → R 1 V 2 → R 2 . . . V t → R t V t + 1 . . . → R l − 1 V l V_1\overset{R_1}{\rightarrow }V_2\overset{R_2}{\rightarrow}...V_t\overset{R_t}{\rightarrow}V_{t+1}...\overset{R_{l-1}}{\rightarrow}V_l V1→R1V2→R2...Vt→RtVt+1...→Rl−1Vl
需要注意的是,元路径中相邻节点的类型是不一样的,即 V i V_i Vi和 V i + 1 V_{i+1} Vi+1属于不同类型的节点, R i R_i Ri表示两个节点间的关系。
以下面的学术网络为例:
上图中,A表示作者节点,P表示论文,O表示作者所属组织,V表示期刊会议。根据上述元路径的定义,可以有以下几种简单的元路径:
- APA:一篇论文中两个作者的合著关系。
- APVPA:两个作者(A)在同一期刊会议(V)上发表了论文。
与node2vec一致,metapath2vec中也给出了每一步的转移概率:

假设当前节点为 v t i v_{t}^i vti,那么下一个节点 v i + 1 v^{i+1} vi+1的选择策略为:
- 如果 v t i v_{t}^i vti与 v i + 1 v^{i+1} vi+1间存在边,且 v i + 1 v^{i+1} vi+1的类型与meta-path的scheme的定义一致(比如APA中,如果当前为P那么下一节点的类型应该为A),那么 v i + 1 v^{i+1} vi+1被选中的概率是均等的,也就是1/节点个数。
- 如果 v t i v_{t}^i vti与 v i + 1 v^{i+1} vi+1间存在边,但 v i + 1 v^{i+1} vi+1的类型与meta-path的scheme的定义不一致,那么不会选择该节点。
- 如果 v t i v_{t}^i vti与 v i + 1 v^{i+1} vi+1间不存在边,那么不会选择该节点。
除了上述三点原则以外,元路径还需遵循对称原则,也就是路径中第一个节点 V 1 V_1 V1和最后一个节点 V l V_l Vl的类型应该一致,即:
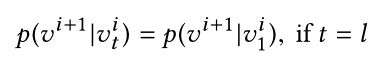
基于元路径的随机游走策略确保了不同类型节点之间的语义关系能够被恰当地整合到skip-gram中。 以下图为例:

在传统的随机游走过程中,从节点CMU过渡到节点 a 4 a_4 a4上的walker的下一步可以是它周围所有类型的节点,即 a 2 a_2 a2、 a 3 a_3 a3、 a 5 a_5 a5、 p 2 p_2 p2、 p 3 p_3 p3和CMU。然而,在meta-path scheme “OAPVPAO”下,下一步选择的节点会偏向于论文节点P。
3. metapath2vec++
metapath2vec中的优化目标为:

其中:
p ( c t ∣ v ; θ ) = e X c t ⋅ X v ∑ u ∈ V e X u ⋅ X v p(c_t|v;\theta)=\frac{e^{X_{c_t}\cdot X_v}}{\sum_{u \in V}e^{X_{u}\cdot X_v}} p(ct∣v;θ)=∑u∈VeXu⋅XveXct⋅Xv
根据要求,我们需要构造节点的邻居函数 N t ( v ) N_t(v) Nt(v)(上下文邻居)。从元路径游走策略可知,metapath2vec中 N t ( v ) N_t(v) Nt(v)是根据meta-path scheme来确定的,然后进行softmax计算时会考虑所有类型的节点,这种方式忽略了softmax中节点的类型信息。换句话说,在进行负采样时,metapath2vec不会区分节点类型,所有类型的节点都有可能被采样到,即上面式子中的 u ∈ V u \in V u∈V,作者认为这样是不合理的。
为此,作者提出了Heterogeneous negative sampling的概念,也就是异质负采样,这不同于一般skip-gram中的负采样,这种采样会考虑节点的类型。
具体来讲就是:

即我们在计算节点向量间的内积并进行softmax时,会根据不同类型的节点的上下文 c t c_t ct进行归一化。简单来讲,如果当前上下文节点类型为 P P P,那么我们只需要将类型为 P P P的节点向量与该上下文节点 c t c_t ct放到一起来求softmax,而不是metapath2vec中的所有节点。
用一个具体的例子来说明,假设序列为 [ A 1 , P 1 , V 1 , P 2 , A 2 ] [A_1,P_1,V_1,P_2,A_2] [A1,P1,V1,P2,A2],我们设中心节点为 V 1 V_1 V1,当前输入的节点为 A 1 A_1 A1,在metapath2vec中,我们会从所有类型的节点(可以为A,也可以为其他类型)中采样一部分与中心节点求内积再求softmax,而在metapath2vec++中,我们只会选择采样一部分作者类型节点(A),然后去更新skip-gram中的参数。
因此,metapath2vec++的优化目标可以定义为:
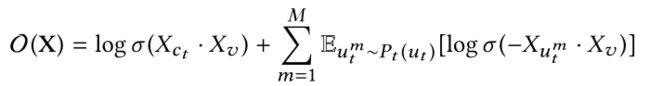
它与metapath2vec的优化目标

相比,只是采样分布变化了一下,一个专注于所有类型节点,一个只考虑与当前节点同类型的节点。从这里我们也可以看出metapath2vec++被提出的根本原因:之前所有方法都是基于同质图,同质图中所有节点类型都一致,因此进行负采样时不需要额外考虑节点类型,而异质图中节点类型不一致,因此自然而然地就会想到负采样时区分节点类型。
4. 实验
baseline:DeepWalk、LINE、PTE以及Spectral Clustering。
5. 小结
本文提出了异质图嵌入模型metapath2vec和metapath2vec++。具体来讲,首先定义了meta-path scheme及其对应的随机游走策略,该策略能够捕获不同类型节点及关系的结构和语义相关性。然后,将随机游走序列输入到本文提出的异质skip-gram中以得到所有类型节点的嵌入表示。需要注意的是,metapath2vec中skip-gram的负采样策略与同质skip-gram一致,考虑了所有节点;而metapath2vec++中skip-gram在进行负采样时只考虑与上下文节点同类型的节点。
大量实验表明,metapath2vec和metapath2vec++学习的潜在特征表示能够改进各种异质网络挖掘任务,如相似性搜索、节点分类和聚类。