SVD(奇异值分解)数值计算方法解析(一)：SVD的概念与人工手算SVD的方法

---

前言

奇异值分解(Singular Value Decomposition，简称SVD)是在现代科学计算中应用广泛的数学算法。
本系列文章《SVD(奇异值分解)数值计算方法解析》将基于笔者的开发经验，从SVD的概念入手，讲解如何人工手算SVD以及如何在计算机上实现SVD，并会在后篇给出详尽的代码与解析。笔者希望读者可以通过阅读这个系列的文章，熟悉SVD数值计算方法完整流程。同时这也是对笔者知识的一种巩固，和知识分享能力的一种锻炼。如果读者发现文章内容有错漏，或是认为部分描述不够清晰，欢迎在评论区提出指导意见。

本篇文章《SVD的概念与人工手算SVD的方法》重在引入SVD的概念，并介绍人工手算SVD的一种方法，笔者希望能通过这种方式让读者对SVD有个简单的了解，方便为后续文章做知识铺垫。如果读者已经熟悉SVD的概念，希望直接了解数值计算SVD的方法，可以关注笔者的后续文章。

---

一、SVD是什么？

1.特征值的定义与特征值分解

在了解SVD之前，我们先从特征值的概念入手。

• 定义：设矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$(本文章仅考虑实数矩阵，不涉及复数矩阵的内容)，如果存在常数$\lambda$和$n$维非零列向量$\mathbf{x}$，使得关系式
  $$\mathbf{A}\mathbf{x}=\lambda \mathbf{x}$$
  成立，则称这样的常数$\lambda$为矩阵$\mathbf{A}$的特征值，称这样的$n$维非零列向量$\mathbf{x}$为矩阵$\mathbf{A}$的特征值向量。
• 特征值分解：设矩阵$\mathbf{A}\in {\mathbb{R}}^{n\times n}$，则必存在正交矩阵
  $$\mathbf{Q}=[{\mathbf{u}}_1,...,{\mathbf{u}}_{\mathbf{n}}]\in {\mathbb{R}}^{n\times n}$$
  使得：
  $$\mathbf{A}=\mathbf{Q}\Sigma {\mathbf{Q}}^{-1}...(1)$$
  我们称式(1)为矩阵$\mathbf{A}$的特征值分解。其中$\Sigma =diag({\lambda }_1,...,{\lambda }_n),({\lambda }_1\ge 0，...，{\lambda }_n\ge 0)$是对角线为矩阵$\mathbf{A}$特征值的$n$阶方阵。${\mathbf{u}}_{\mathbf{i}}$是对应矩阵$\mathbf{A}$特征值${\lambda }_i$的特征列向量，满足$\mathbf{A}{\mathbf{u}}_{\mathbf{i}}={\lambda }_i{\mathbf{u}}_{\mathbf{i}}$。矩阵$\mathbf{Q}$称为矩阵$\mathbf{A}$特征矩阵。
  由于$\mathbf{Q}$是正交矩阵，满足${\mathbf{Q}}^{-1}={\mathbf{Q}}^T$，因此矩阵$\mathbf{A}$的特征值分解也可表示为$\mathbf{A}=\mathbf{Q}\Sigma {\mathbf{Q}}^T.$

关于特征值的含义与作用，本文不做介绍，读者可以自行查阅资料了解。

2.奇异值的定义与奇异值分解

在特征值的定义中，我们注意到假设的矩阵是$n$阶方阵。而当舍去这个限定条件时，我们便可引申出奇异值的概念。

• 定义：设矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$，则称矩阵${\mathbf{A}}^T\mathbf{A}$的特征值的非负平方根为矩阵$\mathbf{A}$的奇异值。$\mathbf{A}$的奇异值的全体记作$\sigma (\mathbf{A})$。

有了奇异值的定义后，我们便可介绍奇异值分解定理。

• 奇异值分解(SVD)：设矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$，则必存在正交矩阵
  $$\mathbf{U}=[{\mathbf{u}}_1,...,{\mathbf{u}}_{\mathbf{m}}]\in {\mathbb{R}}^{m\times m}和\mathbf{V}=[{\mathbf{u}}_1,...,{\mathbf{u}}_{\mathbf{n}}]\in {\mathbb{R}}^{n\times n}$$
  使得：
  $${\mathbf{U}}^T\mathbf{A}\mathbf{V}=\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right](或\mathbf{A}=\mathbf{U}\left[\begin{array}{cc}{\Sigma }_{\mathbf{r}}& 0\\ 0& 0\end{array}\right]{\mathbf{V}}^T)...(2)$$
  我们称式(2)为矩阵$\mathbf{A}$的奇异值分解。其中${\Sigma }_{\mathbf{r}}=diag({\sigma }_1,...,{\sigma }_r),{\sigma }_1\ge ...\ge {\sigma }_r>0.(0\le r\le min(m,n))$。${\sigma }_i$是矩阵$\mathbf{A}$的从大到小排序的第$i$个奇异值。列向量${\mathbf{u}}_{\mathbf{i}}$和${\mathbf{v}}_{\mathbf{i}}$分别称为矩阵$\mathbf{A}$对应奇异值${\sigma }_i$的左奇异向量和右奇异向量，满足$\mathbf{A}{\mathbf{v}}_{\mathbf{i}}={\sigma }_i{\mathbf{u}}_{\mathbf{i}}$。正交矩阵$\mathbf{U}$和$\mathbf{V}$分别称为矩阵$\mathbf{A}$的左奇异矩阵和右奇异矩阵。

关于SVD的应用，本文不做介绍，读者可以自行查阅资料了解。

3.SVD展示

我们可以直接参考pytorch的svd算子官方文档内容。下图为pytorch的svd算子的接口：

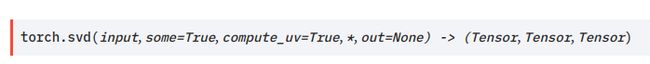
下方代码为pytorch的svd算子官方文档内示例：

>>> a = torch.randn(5, 3)
>>> a
tensor([[ 0.2364, -0.7752,  0.6372],
        [ 1.7201,  0.7394, -0.0504],
        [-0.3371, -1.0584,  0.5296],
        [ 0.3550, -0.4022,  1.5569],
        [ 0.2445, -0.0158,  1.1414]])
>>> u, s, v = torch.svd(a)
>>> u
tensor([[ 0.4027,  0.0287,  0.5434],
        [-0.1946,  0.8833,  0.3679],
        [ 0.4296, -0.2890,  0.5261],
        [ 0.6604,  0.2717, -0.2618],
        [ 0.4234,  0.2481, -0.4733]])
>>> s
tensor([2.3289, 2.0315, 0.7806])
>>> v
tensor([[-0.0199,  0.8766,  0.4809],
        [-0.5080,  0.4054, -0.7600],
        [ 0.8611,  0.2594, -0.4373]])
>>> torch.dist(a, torch.mm(torch.mm(u, torch.diag(s)), v.t()))
tensor(8.6531e-07)
>>> a_big = torch.randn(7, 5, 3)
>>> u, s, v = torch.svd(a_big)
>>> torch.dist(a_big, torch.matmul(torch.matmul(u, torch.diag_embed(s)), v.transpose(-2, -1)))
tensor(2.6503e-06)

pytorch的svd算子详情可查看官方文档：
https://pytorch.org/docs/stable/generated/torch.svd.html?highlight=svd#torch.svd

---

二、人工计算SVD方法

在第一节中，我们给出了SVD的定义，但定理只说明了存在性，并没有给出求解的算法。如果我们希望计算矩阵的奇异值分解，应该如何操作呢？本节将以一个简单的矩阵作为例子，通过手算演示人工计算SVD的一个方法。

• 注意：如果你想直接了解SVD的数值计算方法，可以跳过本节内容。

1.奇异值分解的性质分析

我们首先回顾奇异值分解定理：

• 奇异值分解定理(SVD)：设矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$，则必存在正交矩阵
  $$\mathbf{U}=[{\mathbf{u}}_1,...,{\mathbf{u}}_{\mathbf{m}}]\in {\mathbb{R}}^{m\times m}和\mathbf{V}=[{\mathbf{u}}_1,...,{\mathbf{u}}_{\mathbf{n}}]\in {\mathbb{R}}^{n\times n}$$
  使得：
  $${\mathbf{U}}^T\mathbf{A}\mathbf{V}=\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right](或\mathbf{A}=\mathbf{U}\left[\begin{array}{cc}{\Sigma }_{\mathbf{r}}& 0\\ 0& 0\end{array}\right]{\mathbf{V}}^T)...(1)$$
  其中${\Sigma }_{\mathbf{r}}=diag({\sigma }_1,...,{\sigma }_r),{\sigma }_1\ge ...\ge {\sigma }_r>0.(0\le r\le min(m,n))$。

我们可以注意到，如果将矩阵$\mathbf{A}$和其自身的转置${\mathbf{A}}^T$做矩阵乘，便可得到：
$$\begin{gathered} {\mathbf{A}\mathbf{A}}^T=({\mathbf{U}\Sigma \mathbf{V}}^T)({\mathbf{V}\Sigma }^T{\mathbf{U}}^T)=\mathbf{U}\Sigma ({\mathbf{V}}^T\mathbf{V}){\Sigma }^T{\mathbf{U}}^T=\mathbf{U}(\Sigma {\Sigma }^T){\mathbf{U}}^T=\mathbf{U}{\Sigma }^2{\mathbf{U}}^T\in {\mathbb{R}}^{m\times m} \\ {\mathbf{A}}^{\mathbf{T}}\mathbf{A}=({\mathbf{V}\Sigma }^T{\mathbf{U}}^T)({\mathbf{U}\Sigma \mathbf{V}}^T)={\mathbf{V}\Sigma }^T({\mathbf{U}}^T\mathbf{U}){\Sigma \mathbf{V}}^T=\mathbf{V}(\Sigma {\Sigma }^T){\mathbf{V}}^T=\mathbf{V}{\Sigma }^2{\mathbf{V}}^T\in {\mathbb{R}}^{n\times n} \end{gathered}$$

也就是说，矩阵$\mathbf{A}$的左右奇异矩阵，分别等于对称方阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$和${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征矩阵。并且$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$和${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征值矩阵${\Sigma }^2$即为矩阵$\mathbf{A}$的奇异值矩阵$\Sigma$的平方。这说明，我们可以通过计算对称方阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$和${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征值分解来间接计算矩阵$\mathbf{A}$的奇异值分解。下文便介绍了一种人工计算特征值分解的方法。

2.特征值分解的人工计算方法

我们回顾一下特征值的定义：

• 定义：设矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$(本文章仅考虑实数矩阵，不涉及复数矩阵的内容)，如果存在常数$\lambda$和$n$维非零列向量$\mathbf{x}$，使得关系式
  $$\mathbf{A}\mathbf{x}=\lambda \mathbf{x}$$
  成立，则称这样的常数$\lambda$为矩阵$\mathbf{A}$的特征值，称这样的$n$维非零列向量$\mathbf{x}$为矩阵$\mathbf{A}$的特征值向量。

我们可以注意到，式$\mathbf{A}\mathbf{x}=\lambda \mathbf{x}$也可以写成$(\mathbf{A}-\lambda \mathbf{E})\mathbf{x}=0$($\mathbf{E}$为和$\mathbf{A}$同阶的单位矩阵)。其中$\mathbf{x}$有非零解的充分必要条件是其系数行列式$|\mathbf{A}-\lambda \mathbf{E}|=0$。注意此时$|\mathbf{A}-\lambda \mathbf{E}|$是一个一元n次的多项式。因此，通过求解多项式$|\mathbf{A}-\lambda \mathbf{E}|$的零解，我们便可得到矩阵$\mathbf{A}$的特征值集合，进一步根据式$\mathbf{A}\mathbf{x}=\lambda \mathbf{x}$计算就可以得到特征矩阵。

• 示例1：设矩阵$\mathbf{A}=\left[\begin{array}{cc}3& 5\\ 5& 3\end{array}\right]$，求其特征值分解。
  解：
  (1)设特征值为$\lambda$，求解多项式方程$|\mathbf{A}-\lambda \mathbf{E}|=0$：
  $$|\mathbf{A}-\lambda \mathbf{E}|=0\Rightarrow \left|\begin{array}{cc}3-\lambda & 5\\ 5& 3-\lambda \end{array}\right|=0\Rightarrow (3-\lambda {)}^2-25=0\Rightarrow (\lambda -8)(\lambda +2)=0\Rightarrow {\lambda }_1=8,{\lambda }_2=-2.$$于是我们得到了矩阵$\mathbf{A}$的特征值矩阵$\Sigma =\left[\begin{array}{cc}8& 0\\ 0& -2\end{array}\right]$。
  (2)通过式$(\mathbf{A}-\lambda \mathbf{E})\mathbf{x}=0$求解特征向量：
  $$(\mathbf{A}-{\lambda }_1\mathbf{E}){\mathbf{x}}_1=0\Rightarrow \left[\begin{array}{cc}3-8& 5\\ 5& 3-8\end{array}\right]{\mathbf{x}}_1=0\Rightarrow \left[\begin{array}{cc}-5& 5\\ 5& -5\end{array}\right]{\mathbf{x}}_1=0\Rightarrow {\mathbf{x}}_1=\left[\begin{array}{c}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right]$$$$(\mathbf{A}-{\lambda }_2\mathbf{E}){\mathbf{x}}_2=0\Rightarrow \left[\begin{array}{cc}3+2& 5\\ 5& 3+2\end{array}\right]{\mathbf{x}}_2=0\Rightarrow \left[\begin{array}{cc}5& 5\\ 5& 5\end{array}\right]{\mathbf{x}}_2=0\Rightarrow {\mathbf{x}}_2=\left[\begin{array}{c}1/\sqrt{2}\\ -1/\sqrt{2}\end{array}\right]$$由此我们便求出了矩阵$\mathbf{A}$的两个特征向量${\mathbf{x}}_1$和${\mathbf{x}}_2$(注意计算时要将特征向量单位化)。
  那么矩阵$\mathbf{A}$的特征矩阵为$\mathbf{Q}=[{\mathbf{x}}_1,{\mathbf{x}}_2]=\left[\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ 1/\sqrt{2}& -1/\sqrt{2}\end{array}\right]$。
  (3)验证：
  $$\mathbf{Q}\Sigma {\mathbf{Q}}^{\mathbf{T}}=\left[\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ 1/\sqrt{2}& -1/\sqrt{2}\end{array}\right]\left[\begin{array}{cc}8& 0\\ 0& -2\end{array}\right]\left[\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ 1/\sqrt{2}& -1/\sqrt{2}\end{array}\right]=\left[\begin{array}{cc}3& 5\\ 5& 3\end{array}\right]=\mathbf{A}$$

3.奇异值分解的人工计算方法

基于上文的铺垫，我们这里直接通过一个简单的例子来展示SVD的求解过程：

• 示例2：设矩阵$\mathbf{A}=\left[\begin{array}{cc}1& 0\\ 2& 1\\ 0& 1\end{array}\right]$，求其奇异值分解。
  解：
  (1)计算矩阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$和${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$：
  $$\begin{gathered} \mathbf{A}{\mathbf{A}}^{\mathbf{T}}=\left[\begin{array}{cc}1& 0\\ 2& 1\\ 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 2& 0\\ 0& 1& 1\end{array}\right]=\left[\begin{array}{ccc}1& 2& 0\\ 2& 5& 1\\ 0& 1& 1\end{array}\right] \\ {\mathbf{A}}^{\mathbf{T}}\mathbf{A}=\left[\begin{array}{ccc}1& 2& 0\\ 0& 1& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 2& 1\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}5& 2\\ 2& 2\end{array}\right] \end{gathered}$$(2)计算矩阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$的特征值分解：
  $$|\mathbf{A}{\mathbf{A}}^{\mathbf{T}}-\lambda \mathbf{E}|=0\Rightarrow \left|\begin{array}{ccc}1-\lambda & 2& 0\\ 2& 5-\lambda & 1\\ 0& 1& 1-\lambda \end{array}\right|=0\Rightarrow \lambda (\lambda -1)(\lambda -6)=0\Rightarrow {\lambda }_1=6,{\lambda }_2=1,{\lambda }_3=0.$$求解$$(\mathbf{A}{\mathbf{A}}^{\mathbf{T}}-{\lambda }_1\mathbf{E}){\mathbf{u}}_1=0\Rightarrow \left[\begin{array}{ccc}-5& 2& 0\\ 2& -1& 1\\ 0& 1& -5\end{array}\right]{\mathbf{u}}_1=0$$得到对应特征值${\lambda }_1=6$的特征向量${\mathbf{u}}_1=\left[\begin{array}{c}2/\sqrt{30}\\ 5/\sqrt{30}\\ 1/\sqrt{30}\end{array}\right]$。同理可得对应特征值${\lambda }_2=1$的特征向量${\mathbf{u}}_2=\left[\begin{array}{c}1/\sqrt{5}\\ 0\\ -2/\sqrt{5}\end{array}\right]$，对应特征值${\lambda }_3=0$的特征向量${\mathbf{u}}_3=\left[\begin{array}{c}2/\sqrt{6}\\ 1/\sqrt{6}\\ -1/\sqrt{6}\end{array}\right]$。
  于是我们得到了矩阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$的特征矩阵$\mathbf{U}=[{\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3]=\left[\begin{array}{ccc}2/\sqrt{30}& 1/\sqrt{5}& 2/\sqrt{6}\\ 5/\sqrt{30}& 0& 1/\sqrt{6}\\ 5/\sqrt{30}& -2/\sqrt{5}& -1/\sqrt{6}\end{array}\right]$。
  (3)计算矩阵${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征值分解：
  $$|{\mathbf{A}}^{\mathbf{T}}\mathbf{A}-\lambda \mathbf{E}|=0\Rightarrow \left|\begin{array}{cc}5-\lambda & 2\\ 2& 2-\lambda \end{array}\right|=0\Rightarrow (\lambda -1)(\lambda -6)=0\Rightarrow {\lambda }_1=6,{\lambda }_2=1.$$求解$$({\mathbf{A}}^{\mathbf{T}}\mathbf{A}-{\lambda }_1\mathbf{E}){\mathbf{v}}_1=0\Rightarrow \left[\begin{array}{cc}-1& 2\\ 2& -4\end{array}\right]{\mathbf{v}}_1=0$$得到对应特征值${\lambda }_1=6$的特征向量${\mathbf{v}}_1=\left[\begin{array}{c}2/\sqrt{5}\\ 1/\sqrt{5}\end{array}\right]$。同理可得对应特征值${\lambda }_2=1$的特征向量${\mathbf{v}}_2=\left[\begin{array}{c}-1/\sqrt{5}\\ 2/\sqrt{5}\end{array}\right]$。
  于是我们得到了矩阵${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征矩阵$\mathbf{V}=[{\mathbf{v}}_1,{\mathbf{v}}_2]=\left[\begin{array}{cc}2/\sqrt{5}& -1/\sqrt{5}\\ 1/\sqrt{5}& 2/\sqrt{5}\end{array}\right]$
  (4)根据矩阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$和${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征值分解结果得到矩阵$\mathbf{A}$的奇异值分解：
  $$\begin{gathered} \mathbf{A}=\mathbf{U}\Sigma {\mathbf{V}}^{\mathbf{T}}=\mathbf{U}\left[\begin{array}{ccc}\sqrt{{\lambda }_1}& 0& \\ 0& \sqrt{{\lambda }_2}& 0\\ 0& 0& 0\end{array}\right]{\mathbf{V}}^T \\ =\left[\begin{array}{ccc}2/\sqrt{30}& 1/\sqrt{5}& 2/\sqrt{6}\\ 5/\sqrt{30}& 0& 1/\sqrt{6}\\ 5/\sqrt{30}& -2/\sqrt{5}& -1/\sqrt{6}\end{array}\right]\left[\begin{array}{ccc}\sqrt{6}& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{cc}2/\sqrt{5}& 1/\sqrt{5}\\ -1/\sqrt{5}& 2/\sqrt{5}\end{array}\right]. \end{gathered}$$

4.总结

通过示例2的展示，我们可以看到手算SVD的步骤主要为：
(1)计算矩阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$和${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$。
(2)计算矩阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$的特征值分解。
(3)计算矩阵${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征值分解。
(4)根据矩阵$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$和${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$的特征值分解结果得到矩阵$\mathbf{A}$的奇异值分解。

但是如果按照上面的算法，使用计算机去计算SVD，就会不可避免地遇到一个问题：计算矩阵的特征值分解时，需要求一元n次多项式方程$|\mathbf{A}-\lambda \mathbf{E}|=0$的解。而计算机通常是直接处理数值数据的，不能像人工计算时那样假设未知数，也就是说计算机是难以通过输入矩阵$\mathbf{A}$和数$\lambda$推导出多项式方程$|\mathbf{A}-\lambda \mathbf{E}|=0$的表达式，更不必论之后的求解了。
那么应该使用什么样的数学方法，才能满足计算机计算的特性，使得矩阵可以在计算机上做SVD求解呢？这一问题，我们将在本系列的下一篇文章进行解答。感谢您阅读本篇文章！