吴恩达《深度学习专项》笔记（十二）：目标检测与语义分割简介 (YOLO, U-Net)

这节课中，我们要学习计算机视觉中最重要的任务之一——目标检测任务。我们会先认识目标定位和关键点检测这两个比较简单的任务，慢慢过度到目标检测任务。之后，我们会详细学习目标检测的经典算法YOLO。最后，我们会稍微认识一下语义分割任务及适用于此问题的U-Net架构。

课堂笔记

目标定位

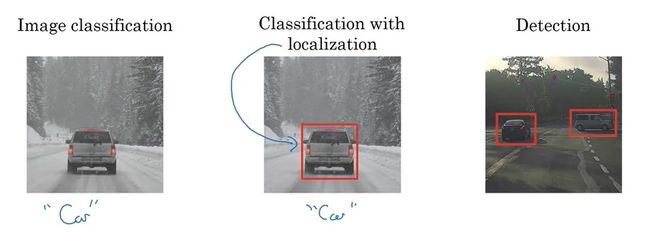
在图像分类问题中，给定一幅图片，我们只要说出图片里的物体是什么就行了。在这堂课要讨论的任务中，我们还要多做一件事——定位。我们要先用边框圈出图中的物体，再说出框里的物体是什么。这叫做带定位(localization)的分类问题。更进一步，如果我们不再是只讨论一个物体，而是要把图片中所有物体都框出来，并标出每一个物体的类别，这就是目标检测问题，

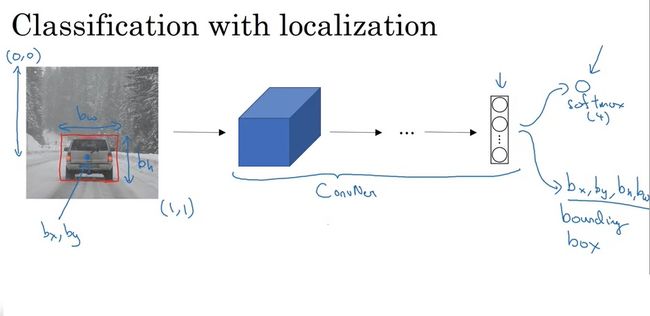
我们对分类任务的神经网络结构已经很熟悉了。那么，带定位的分类该使用怎样的网络呢？实际上，一个边框可以用边框中心和边框宽高这四个量表示。除了softmax出来的分类结果外，我们只要让网络再多输出四个数就行了。如下图所示：

这里，要统一一下对于边框的定义。我们用$b_x,b_y$表示边框的中心坐标，$b_h,b_w$表示边框的高、宽。

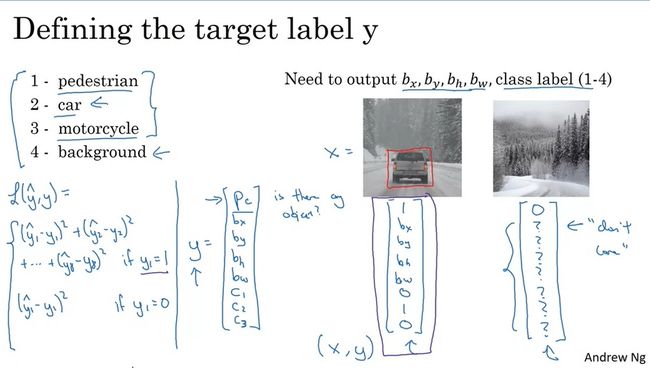
来看一下标签$y$的具体写法。假设一共有四类物体：行人、汽车、摩托车、背景（没有物体）。那么，标签$y$应该用$y=[p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3{]}^T$表示。其中，$p_c$表示图中有没有物体。若$p_c=1$，则$c_1,c_2,c_3$分别表示物体属于除背景外的哪一类；若$p_c=0$，则其他值无意义。

这样，在算误差时，也需要分类讨论。若$p_c=1$，则算估计值与标签8个分量两两之间的均方误差；若$p_c=0$，只算$p_c$的均方误差，不用管其他量。

只要更换一下神经网络的输出格式，我们就能得到一个完成目标定位问题的网络。

关键点检测

我们刚刚学了用2个点表示一个边框。其实，拓展一下边框检测，就是一个关键点（英文有时叫做"landmark"，是“地标”的意思）检测问题。

比如，在人脸关键点检测中，我们可以定义一堆关键点，分别表示眼睛、鼻子、嘴巴……的位置。我们还是让网络先输出一个数，表示图中有没有人脸；再输出2n个数，表示n个人脸关键点。这样，网络就能学习怎么标出人脸关键点了。

很多应用都基于人脸关键点检测技术。比如我们检测到了眼睛周围的关键点后，就可以给人“戴上”墨镜。

总之，通过这一节的学习，我们要知道，目标定位中输出2个坐标只是关键点检测的一个特例。只要训练数据按照某种规律标出了关键点，不管这些关键点是表示一个框，还是人脸上各器官的位置，网络都能学习这种规律。

目标检测

有了之前的知识储备，现在我们来正式学习目标检测。目标检测可以用一种叫做“滑动窗口”的技术实现。

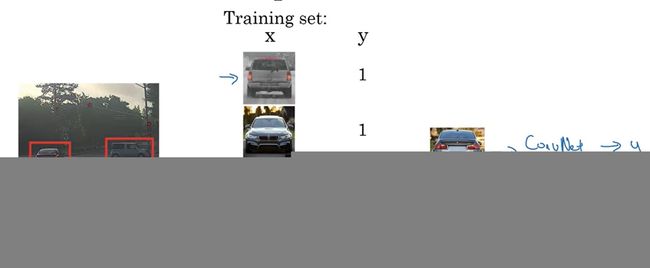
假设我们要构建一个汽车的目标检测系统。我们可以先构造一个汽车分类数据集——数据集的x是一些等大的图片，y表示图片里是不是有汽车。如果图片里有汽车，汽车应该占据图片的大部分位置。

通过学习，网络就能够判断一个框里的物体是不是汽车了。这样，我们可以用一个边框框出图片的一部分，裁剪下来，让网络看看图片的这一部分是不是汽车。只要我们尝试的次数够多，总能找出图中的汽车。

在遍历边框时，我们是通过“滑动”的方法：遍历边框的大小，选择好大小后把框放到左上角，先往右移，再往下移。所以这种方法叫做“滑动窗口”。

滑动窗口算法有一个缺点：如果我们移动窗口的步伐过小，则运行分类器的次数会很多；如果移动窗口的步伐过大，则算法的精度会受到影响。在深度学习时代之前，分类器都是一些简单的线性函数，能够快速算完，多遍历一些滑动窗口没有问题。而使用了深度CNN后，遍历滑动窗口的代价就很大了。

幸好，滑动窗口也可以通过卷积来生成，而不一定要遍历出来。让我们看下去。

基于卷积的滑动窗口

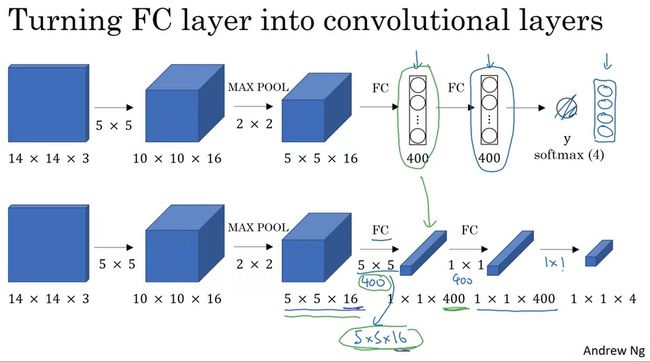
滑动窗口其实可以通过执行巧妙的卷积来生成。在那之前，我们先学一门前置技能：怎么把全连接层变成卷积层。

前两周学习CNN时，我们学过，卷积结束后，卷积的输出会被喂入全连接层中。实际上，我们可以用卷积来等价实现全连接层。比如下图中，一个$5\times 5\times 16$的体积块想变成一个长度为400的向量，可以通过执行400个$5\times 5$的卷积来实现。

知道了这一点后，我们就可以利用卷积来快速实现滑动窗口了。

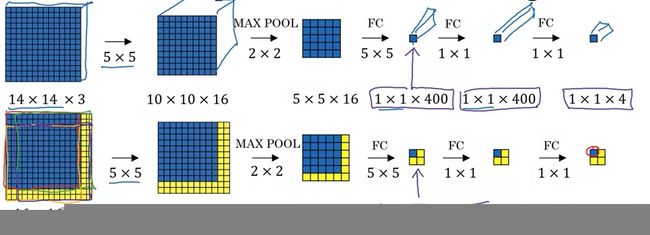
假设我们按照上一节的算法，先实现了对$14\times 14$的小图片进行分类的分类器。之后，我们输入了一张$16\times 16$的大图片。我们遍历滑动窗口，令步幅为2。这样，理论上，有4个合法的滑动窗口，应该执行4次分类器的运算，如下图所示：

可是，仔细一想，在执行4次分类器的过程中，有很多重复的运算。比如，对于4个滑动窗口中间那共有的$12\times 12$个像素，它们的卷积结果被算了4次。理想情况下，只需要对它们做一次卷积就行了。这该怎么优化呢？

其实，很简单，我们可以利用卷积本身的特性来优化。卷积层只定义了卷积核，而没有规定输入图像的大小。我们可以拿出之前在$14\times 14$的图像上训练好的卷积层，把它们用在$16\times 16$的图片的卷积上。经过相同的网络，$16\times 16$的图片会生成一个$2\times 2$大小的分类结果，而不是$1\times 1$的。这$2\times 2$个分类结果，恰好就是那4个滑动窗口的分类结果。通过这样巧妙地利用卷积操作，我们规避了遍历滑动窗口带来的重复计算。

不过，这个方法还是有一些缺陷的。在刚才那个例子中，$16\times 16$的图片其实可以放下9个$14\times 14$大小的边框。但是，由于分类网络中max pool的存在，我们只能生成4个分类结果，也就是步幅为2的滑动窗口的分类结果。同时，最准确的检测框也不一定是正方形的，而可能是长方形的。为了让生成的滑动窗口更准确一些，我们要用到其他方法。

预测边框

在这一节，我们要使用YOLO(You Only Look Once)算法解决上一节中碰到的问题。还记得这周课开头学的目标定位问题吗？我们可以把滑动窗口和目标定位结合一下。

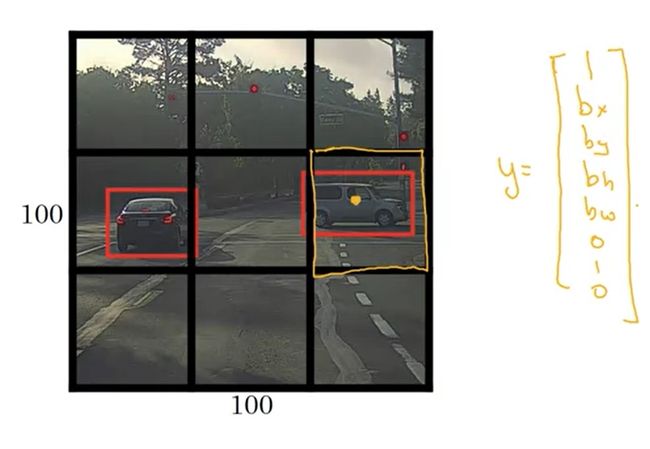
给定一幅图像，我们可以把图像分成$3\times 3$个格子。训练模型前，我们要对训练数据做预处理。根据每个训练样本中物体的中心点所在的格子，我们把物体分配到每一个格子中。也就是说，不管一个物体的边框跨越了几个格子，它的中心点在哪，它就属于哪个格子。比如对于下图的训练样本，右边那辆车就属于橙色的格子。之后，我们给每个格子标上标签$y$。这个标签$y$就是目标定位中那个表示图片中是否有物体、物体的边框、物体的类别的标签向量。对于这个$3\times 3$的格子，有9个标签向量，整个标签张量的形状是$3\times 3\times 8$。

这样，每一幅图像的输出和标签一样，也是一个$3\times 3\times 8$的张量了。输入一幅图片后，我们利用上一节学的卷积滑动窗口，同时预测出每个格子里的物体边框。

另外，这里要详细讨论一下$b_x,b_y,b_h,b_w$的表示方法。由于我们只关心框相对于格子的位置，因此我们可以把规定一个格子的边长为1。这样，就满足$0\le b_x,b_y\le 1$了。不过，由于物体的边框可以超出小框，$b_h,b_w>1$是很有可能的。

看到这，大家可能会有一些疑问：如果一个格子里有多个物体呢？的确，这个算法无法输出一个格子里的多个物体。一种解决方法是，我们可以把格子分得更细一点，比如$19\times 19$个格子。这样，可以被检测到物体会多一些。但是，增加格子数又会引入一个新的问题——多个格子检测到了同一个物体。下面的两节里我们会尝试解决这个新的问题。

吴恩达老师说，YOLO这篇论文很难读懂，他和其他几个资深研究者都花了很大的功夫才读懂这篇论文。

IoU(交并比)

在目标检测中，有一个微妙的问题：框出一个物体的边框有无数个，想精确框出标签的边框是不可能的。怎么判定一个输出结果和标签里的边框“差不多”呢？这就要用到IoU(Intersection over Union，交并比) 这个概念。

IoU，顾名思义，二者的交集比上二者的并集，很好理解。比如下图中，网络的输出是紫框，真值是红框。二者的并集是绿色区域，交集是橙色区域。则IoU就是橙色比绿色。

依照惯例，如果IoU$\ge 0.5$，我们就认为网络的输出是正确的。当然，想更严格一点，0.6,0.7也是可以的。

IOU 也是 "I owe you(我欠了你的钱)"的缩写，哈哈哈。

NMS(非极大值抑制)

假设在YOLO中，我们用$19\times 19$个小格来检测物体。可是，由于小格子太多了，算法得到了多个重复的检测框（以及每个框中有物体的概率）。这该怎么办呢？

NMS(Non-Maximum Suppresion，非极大值抑制)就是解决这个问题的算法。这个算法的名字听起来很奇怪，但大家理解了这个算法的实现后，就知道这个“抑制”是什么意思了。

讲起算法我就不困了。我会抛弃视频中的讲解思路，用我自己的逻辑讲一遍。讲算法，千万不能一上来就讲算法的步骤，一定要先讲清楚算法的思路。

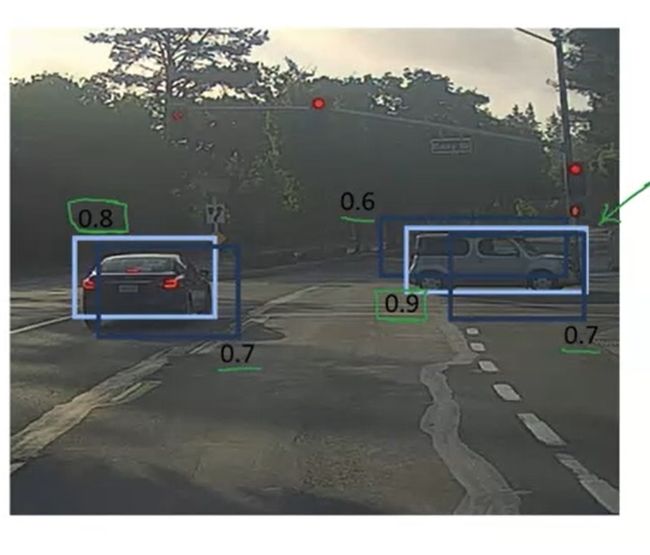
在学NMS之前，我们先动动脑，看看在去掉重复的框时，我们期望得到怎样的去重输出结果。

首先，既然是去重，那么就不能出现两个框过度重合的情况。其次，我们希望留下来的框的预测概率尽可能大。

在这两个要求下，我们来看看上面那幅图的输出应该是怎样的。
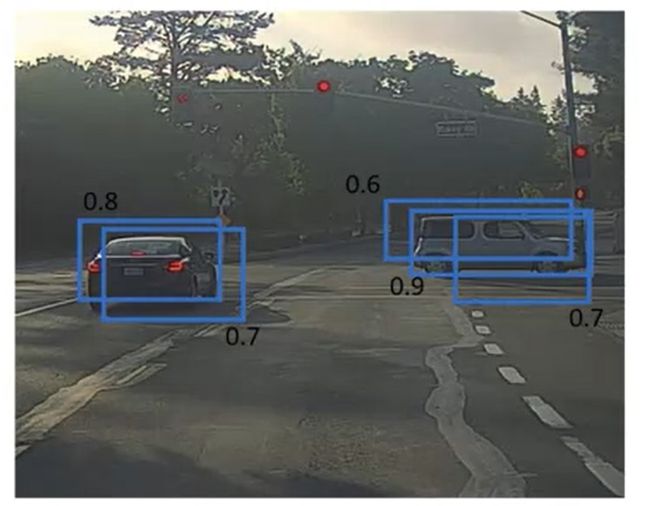
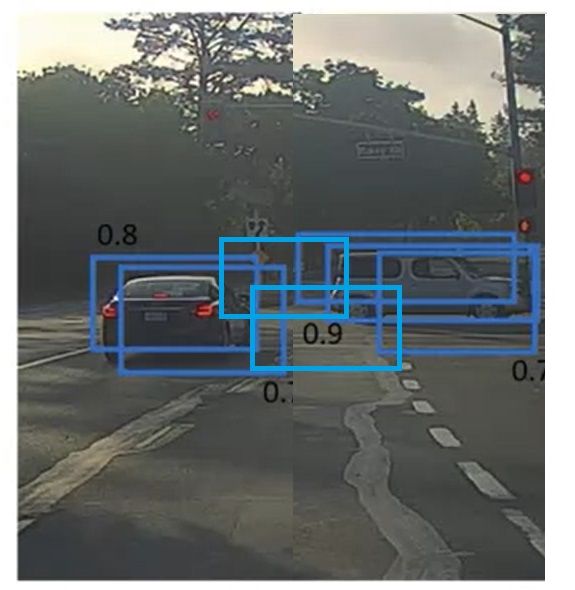
我们一眼就能看出，对于左边那辆车，我们应该保留0.8的框；对于右边那辆车，我们应该保留0.9的框。

为什么我们能“一眼看出”呢？这是因为左边两个框、右边三个框恰好都分别表示了一辆车。我们能够快速地把这些框分成两类。但是，在情况比较复杂时，我们就难以快速找出最好的框了。比如下面这种情况中，两辆车很近，有些框甚至同时标出了两辆车：

为了处理这种复杂的情况，我们必须想出一种万全的算法，以筛选出那些概率比较大的框。

稍微思考一下，其实这样的算法非常简单：找出最大的框，去掉所有和它过度重合的框；在剩下的框中，找出最大的框，去掉所有和它过度重合的框；……。一直重复直到没有未处理的框为止。这就是NMS算法。

还是让我们来看看刚刚那个例子。使用NMS时，我们会先找到0.9这个框，“抑制”掉右边0.6和0.7的框。在剩下的框中，最大的是0.8这个框，它会“抑制”掉左边那个0.7的框。

接下来，让我们来严格描述一下这个算法。假设我们有$19\times 19=361$个输出结果，每个输出结果是一个长度为5的向量$[p_c,b_x,b_y,b_h,b_w]$，分别表示有物体的概率、边框的中心和高宽（我们先不管检测多个物体的情况。事实上，当推广到多个物体时，只要往这个输出结果里多加几个概率就行了）。我们要用NMS输出应该保留的检测结果。“过度重合”，就是两个框的IoU大于0.5。

首先，先做一步初筛，扔掉概率$p_c$小于0.6的结果。

之后，对于没有遍历的框，重复执行：找出概率最大的框，把它加入输出结果；去掉所有和它IoU大于0.5的框。

这个过程用伪代码表示如下：

# Input and preprocessing
input predicts of size [19, 19, 5]
resize predicts to [361, 5]

# Filter predicts with low probability
filtered_predicts = []
for predict in predicts:
    # drop p_c < 0.6
    if predict[0] >= 0.6:  
        filtered_predicts.append(predict)

# NMS
n_remainder  = len(filtered_predicts)
vis = [False] * n_remainder # False for unvisited item
output_predicts = []
while n_remainder > 0:
    max_pro = -1
    max_index = 0
    # Find argmax
    for i, p in enumerate(filtered_predicts):
        if not vis[i]:
            if max_pro < p[0]:
                max_index = i
                max_pro = p[0]

    # Append output
    max_p = filtered_predicts[max_index]
    output_predicts.append(max_p)

    # Suppress
    for i, p in enumerate(filtered_predicts):
        if not vis[i] and i != max_index:
            if get_IoU(p[1:5], max_p[1:5]) > 0.5:
                vis[i] = True
                n_remainder -= 1
    vis[max_index] = True
    n_remainder -= 1

假设进NMS的框有$N$个。算法里求当前最大框那一步可以用优先队列来优化，这一步复杂度是$O(logN)$。但是“抑制”那一步必须要遍历一遍剩下的框，还是有一个$O(N)$复杂度（我暂时想不出朴素的低复杂度的算法）。因此，不用优先队列优化也差不多。算上外层的循环，整个算法的复杂度是$O(N^2)$。在实际的应用中，送入NMS的结果没那么多，不会超过10000个。而且，随着框被不断过滤，外层循环的次数会减少不少。这个算法的性能瓶颈不在输入数$N$上，而在于求IoU实现的细节上。

锚框（Anchor Boxes)

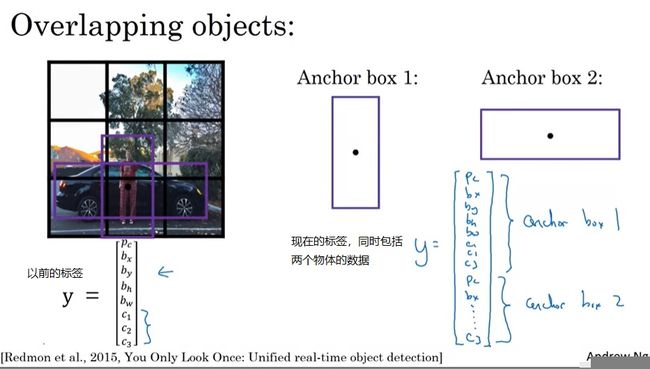
为了让一个格子能够检测到多个物体，YOLO论文还提出了一种叫做锚框(Anchor Boxes)的技术。

假设一个格子里同时包含了两个物体：一个“竖着”的人和一个“横着”的车。那么，我们可以以这个格子的中心点为“锚”，画一个竖的框和横的框，让每个格子可以检测到两个物体。这样，人和车都能被检测了。

严谨地描述，锚框技术是这样做改进的：

• 之前，每一个格子只能包含一个样本。训练数据中每一个标签框会被分配到它中点所在的格子。
• 现在，每一个格子能包含多个样本。每个格子都会预定义几个不同形状的锚框，有几个锚框，就最多能检测到几个物体。训练数据的每一个标签框会被分配到和它交并比最大的的锚框。

注意，之前的最小单元是格子，现在是锚框，所以说现在每个样本被分配到锚框上而不是格子上。可以看下面这两个样本的例子，第一个例子是两个物体都检测到了，第二个是只有锚框2里有物体。和之前一样，如果有某个锚框里没有物体，则除了$p_c$外全填问号即可。

锚框技术实际上只是对训练数据做了一个约束，改变了训练数据的格式。检测算法本身没有什么改变。

YOLO 算法总结

让我们把前几节的内容总结一下，看一下YOLO算法的全貌。

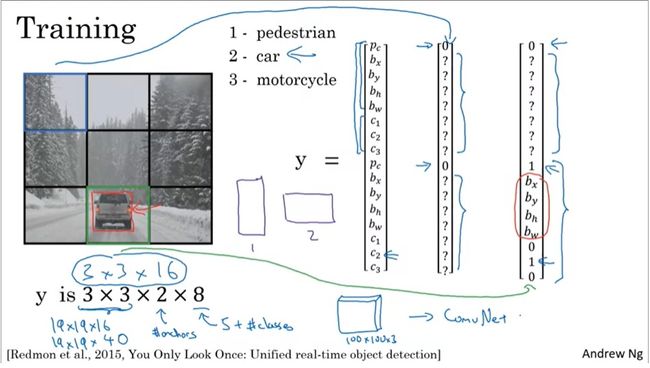
在训练前，我们要对数据做预处理。首先，我们要指定以下超参数：图片切分成多大的格子、每个格子里有多少个锚框。之后，根据这些信息，我们可以得到每一个训练标签张量的形状。比如$3\times 3\times 2\times 8$的一个训练标签，表示图片被切成了$3\times 3$的格子，每个格子有两个锚框。这是一个三分类问题，对于每一个检测出来的物体，都可以用一个长度为$8$的向量表示。其中，$p_c$表示这个锚框里有没有物体, $(b_x,b_y),(b_h,b_w)$分别表示中心点坐标、框的高宽，$c_1,c_2,c_3$分别表示是否该类物体。

有了预处理好的训练数据，就可以训练一个CNN了。

在网络给出了输出后，由于输出的框往往多于标签中的框，还要对输出结果进行筛选。筛选的过程如前文所述，先去掉概率过小的框，再分别对每一类物体的框做NMS。

区域提案

YOLO算法是在一堆固定的框里找物体。实际上，我们还可以用神经网络来找出候选框，再在这些框里详细检测。这种技术就叫做区域提案(region proposal)，相关的网络叫做R-CNN(Region with CNN)。

R-CNN 系列网络有多个改进版本：

• R-CNN: 使用区域提案，但是每次只对一个区域里的物体做分类。
• Fast R-CNN: 使用区域提案，并使用基于卷积的滑动窗口加速各区域里物体的分类。
• Faster R-CNN: 前两个算法都是用传统方法提案区域，Faster R-CNN用CNN来提案区域，进一步令算法加速。

吴恩达老师认为，虽然区域提案的方法很酷，但把目标检测分两步来完成还是太麻烦了，一步到位的YOLO系列算法已经挺方便了。

基于U-Net的语义分割

最早这门课是没有这一节的，估计U-Net的架构太常用了，吴恩达老师把基于U-Net的语义分割加入了这周的课中。

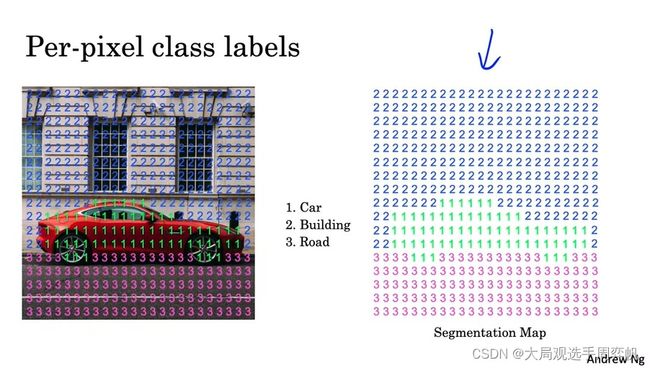
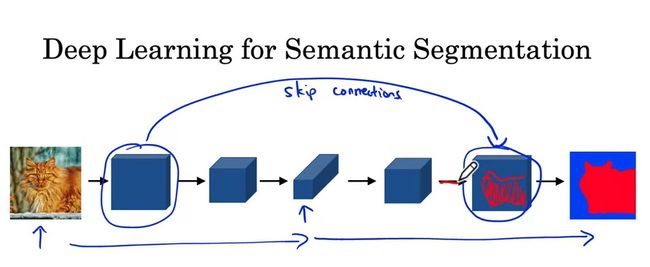
语义分割也是应用非常广泛的一项CV任务。相较于只把物体框出来的目标检测，语义分割会把每一类物体的每个像素都精确地标出来。如下图的示例所示，输入一张图片，语义分割会把每一类物体准确地用同一种颜色表示。

具体来说，语义分割的输出是一个单通道图片。图片的数字表示此处像素的类别。

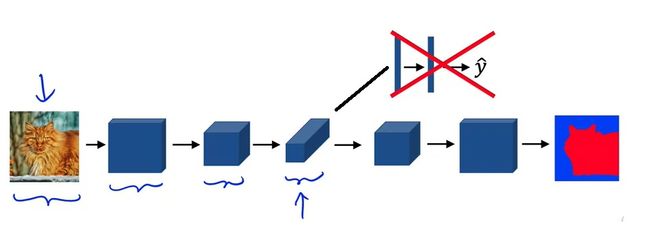
在分类模型中，图像会越卷越小，最后压平放进全连接层并输出多个类别的分类概率。而在语义分割模型中，由于模型的输出也是一幅图像，在输入图像被卷小了以后，应该还有一个放大的过程。

目前，我们还没有学过带学习参数的可以放大图像分辨率的结构。下一节介绍的反卷积能够完成这件事。

反卷积

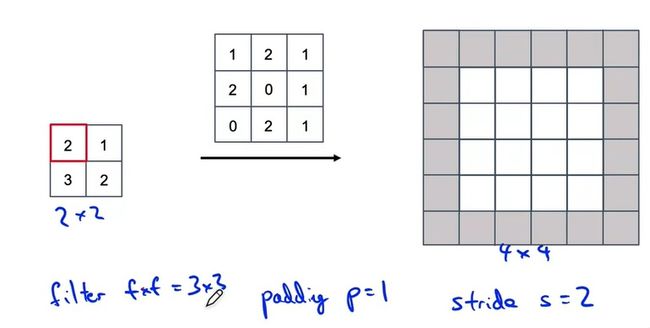
反卷积和卷积的输入输出大小彻底相反。让我们看看反卷积的形状是怎么计算的。

如上图所示，反卷积也有卷积核大小、步幅、填充这些参数。不过这些参数都是在输出图像上做的。也就是说，我们会在输出图像上做填充，并且每次在输出图像上一步一步移动。我们把正卷积的输出大小计算公式套到反卷积上的输出上，就能算出反卷积的输入的大小。

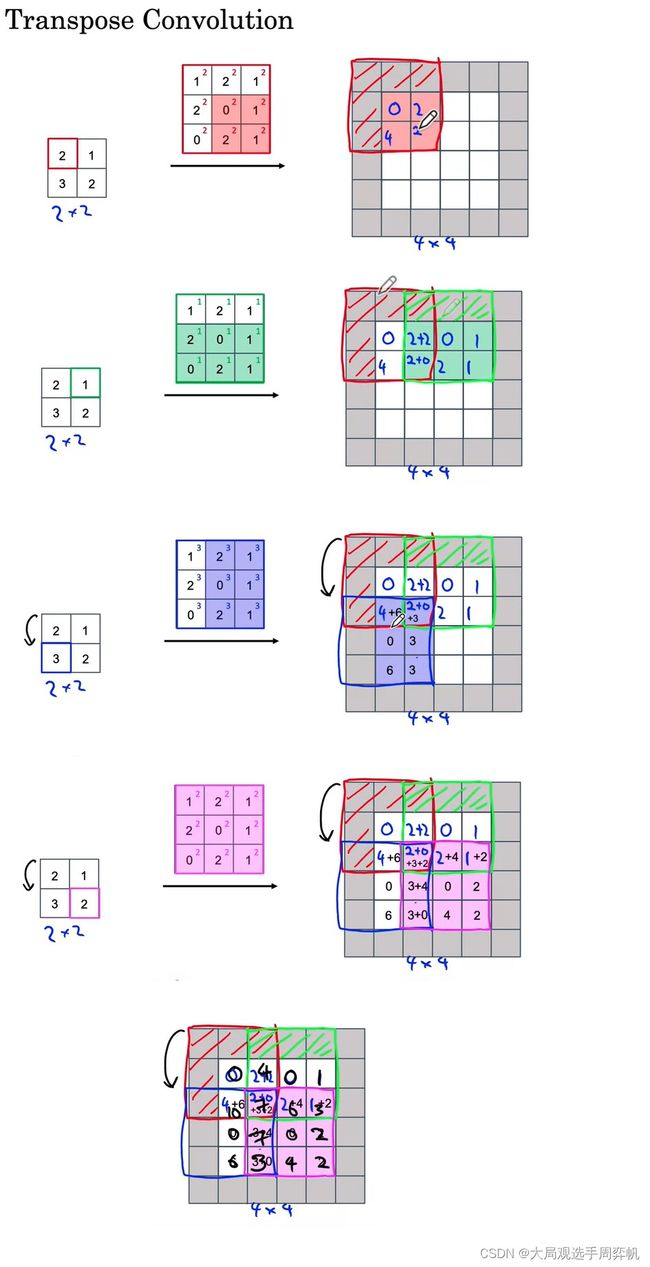
在卷积时，我们是把卷积核与图像对应位置的数字乘起来，再求和，算出一个输出值；反卷积则是反了过来，把一个输入值乘到卷积核的每个位置上，再把乘法结果放再输出的对应位置上。一趟反卷积计算如下图所示：

这里我们只需要知道反卷积可以做上采样就行了，不需要纠结底层实现细节。

本课对反卷积的介绍甚少。实际上，反卷积可以通过正卷积来实现。我扫了一圈没看到讲解得比较好的相关文章，有兴趣的可以自行查找资料。

U-Net 架构

学完了反卷积，可以来看U-Net的结构了。

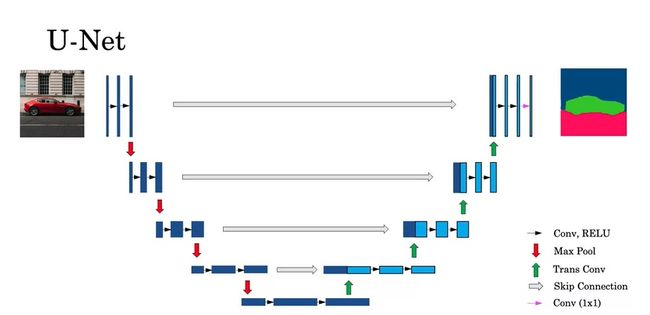
U-Net除了对图像使用了先缩小再放大的卷积外，还使用了一种跳连（不是ResNet中残差连接的跳连，而是把两份输入拼接在了一起）。这样，在反卷积层中，不仅有来自上一层的输入，还有来自前面相同大小的正卷积的结果。这样做的好处是，后半部分的网络既能获得前一个卷积的抽象、高级（比如类别）的输入，又能获得前半部分网络中具体，低级的特征（比如形状）。这样，后面的层能够更好地生成输出。

U-Net具体的结构如下：

这幅图中，做运算的图像张量被表示成了一个二维矩形，矩形的高度是图像的宽高，矩形的宽度是通道数。U-Net的前半部分和常见的CNN一样，缩小图像大小，增大图像通道数。而在后半部分中，每次上采样时，一半的通道来自上一层的输出，另一半的通道来自于网络前半部分。

从图中能看出，U-Net的结构图是一个“U”型，因此它才被叫做U-Net。

总结

在这篇文章中，我们主要学习了以下内容：

• 任务定义与输出格式
  • 目标定位
  • 关键点检测
  • 目标检测
  • 语义分割
• YOLO
  • 用卷积实现全连接
  • 用卷积实现滑动窗口
  • 锚框
  • IoU
  • NMS
  • YOLO算法
• U-Net
  • 反卷积
  • U-Net架构