有限元方法求解一维扩散方程(FEALPy)
有限元方法求解一维扩散方程
文章目录
- 有限元方法求解一维扩散方程
-
- 有限元方法推导
- 差分格式的介入
- 数值算例
之前完成了 FEALPy 有限元求解 Poisson 方程 的数值算例, 通过 湘潭大学王唯师兄的协助, 今天基于 FEALPy 运用有限元方法求解一个抛物型方程,为说明使用方法而又简单起见,于是理论部分专注于讨论下面这个一维的抛物型方程:
∂ u ∂ t − a ∂ 2 u ∂ x 2 = f ( x , t ) , ( x , t ) ∈ ( 0 , 1 ) × ( 0 , T ] u ( x , 0 ) = ψ ( x ) , x ∈ [ 0 , 1 ] u ( 0 , t ) = u ( 1 , t ) = 0 , t ∈ [ 0 , T ] \begin{aligned} &\frac{\partial u}{\partial t}-a \frac{\partial^{2} u}{\partial x^{2}}=f(x, t), \quad(x, t) \in(0,1) \times(0, T] \\ &u(x, 0)=\psi(x), x \in[0,1] \\ &u(0, t)=u(1, t)=0, t \in[0, T] \end{aligned} ∂t∂u−a∂x2∂2u=f(x,t),(x,t)∈(0,1)×(0,T]u(x,0)=ψ(x),x∈[0,1]u(0,t)=u(1,t)=0,t∈[0,T]
有限元方法推导
有限元方法相对于有限差分方法的一个巨大优势在于:对于复杂的几何区域, 网格可以画得非常 随意, 而有限差分法的格式需要建立在规则的网格上.
幸运的是, 复杂区域只存在于空间上, (通常) 并没有“复杂的时间区域” 这一说法, 毕竟时间是一维的, 一维空间上的连通区域都相似于直线、线段、射线之一, 都是相当简单的几何.
也就是说, 在时间轴上或许可以继续沿用有限差分法, 而在空间上采用有限元的方法.
回忆一下用有限元求解的 hello world 模型, 椭圆型问题:
− a ∂ 2 u ∂ x 2 = f ( x ) , x ∈ ( 0 , 1 ) u ( 0 ) = u ( 1 ) = 0 \begin{aligned} &-a \frac{\partial^{2} u}{\partial x^{2}}=f(x), \quad x \in(0,1) \\ &u(0)=u(1)=0 \end{aligned} −a∂x2∂2u=f(x),x∈(0,1)u(0)=u(1)=0
是将其转化为弱形式, 找一个 u ∈ H 0 1 ( 0 , 1 ) u \in H_{0}^{1}(0,1) u∈H01(0,1), 使得:
a ∫ 0 1 v ′ u ′ d x = ∫ 0 1 f v d x a \int_{0}^{1} v^{\prime} u^{\prime} d x=\int_{0}^{1} f v d x a∫01v′u′dx=∫01fvdx
对任意的 v ∈ H 0 1 ( 0 , 1 ) v \in H_{0}^{1}(0,1) v∈H01(0,1) 成立来达成的.
具体而言, 是构造一组基于空间的基函数, 使得解在基函数构成的空间中被逼近, 也就是
u ( x ) = ∑ i = 0 N c i ϕ i ( x ) u(x)=\sum_{i=0}^{N} c_{i} \phi_{i}(x) u(x)=i=0∑Nciϕi(x)
每一个基函数的系数是固定的, 而对于今天这个时间依赖的抛物问题, 那就构造随时间变化的系数来表示好了, 也就是
u ( x , t ) = ∑ i = 0 N c i ( t ) ϕ i ( x ) u(x, t)=\sum_{i=0}^{N} c_{i}(t) \phi_{i}(x) u(x,t)=i=0∑Nci(t)ϕi(x)
再用弱形式写一下, 就是找到上面的 u \mathrm{u} u, 使得对任意 v ∈ H 0 1 ( 0 , 1 ) v \in H_{0}^{1}(0,1) v∈H01(0,1), 都有
∫ 0 1 v ( x ) ∂ u ∂ t d x − a ∫ 0 1 v ( x ) ∂ 2 u ∂ x 2 d x = ∫ 0 1 f ( x , t ) v ( x ) d x \int_{0}^{1} v(x) \frac{\partial u}{\partial t} d x-a \int_{0}^{1} v(x) \frac{\partial^{2} u}{\partial x^{2}} d x=\int_{0}^{1} f(x, t) v(x) d x ∫01v(x)∂t∂udx−a∫01v(x)∂x2∂2udx=∫01f(x,t)v(x)dx
运用分部积分公式换一换, 得到
∫ 0 1 v ( x ) ∂ u ∂ t d x + a ∫ 0 1 v ′ ( x ) ∂ u ∂ x d x = ∫ 0 1 f ( x , t ) v ( x ) d x \int_{0}^{1} v(x) \frac{\partial u}{\partial t} d x+a \int_{0}^{1} v^{\prime}(x) \frac{\partial u}{\partial x} d x=\int_{0}^{1} f(x, t) v(x) d x ∫01v(x)∂t∂udx+a∫01v′(x)∂x∂udx=∫01f(x,t)v(x)dx
然后由于对于固定的t, 上式的成立也等价于
∑ i = 0 N ( c i ′ ( t ) ∫ 0 1 ϕ j ( x ) ϕ i ( x ) d x + a ⋅ c i ( t ) ∫ 0 1 ϕ j ′ ( x ) ϕ i ′ ( x ) d x ) = ∫ 0 1 f ( x , t ) ϕ i ( x ) d x \sum_{i=0}^{N}\left(c_{i}^{\prime}(t) \int_{0}^{1} \phi_{j}(x) \phi_{i}(x) d x+a \cdot c_{i}(t) \int_{0}^{1} \phi_{j}^{\prime}(x) \phi_{i}^{\prime}(x) d x\right)=\int_{0}^{1} f(x, t) \phi_{i}(x) d x i=0∑N(ci′(t)∫01ϕj(x)ϕi(x)dx+a⋅ci(t)∫01ϕj′(x)ϕi′(x)dx)=∫01f(x,t)ϕi(x)dx
写成矩阵形式
A C ′ ( t ) + a K C ( t ) = F ( t ) A C^{\prime}(t)+a K C(t)=F(t) AC′(t)+aKC(t)=F(t)
其中
- C ( t ) = [ c 0 ( t ) , c 1 ( t ) , ⋯ , c N ( t ) ] C(t)=\left[c_{0}(t), c_{1}(t), \cdots, c_{N}(t)\right] C(t)=[c0(t),c1(t),⋯,cN(t)], 基函数系数
- A = [ ∫ 0 1 ϕ i ϕ j d x ] i j A=\left[\int_{0}^{1} \phi_{i} \phi_{j} d x\right]_{i j} A=[∫01ϕiϕjdx]ij, 称为质量矩阵
- K = [ ∫ 0 1 ϕ i ′ ϕ j ′ d x ] i j K=\left[\int_{0}^{1} \phi_{i}^{\prime} \phi_{j}^{\prime} d x\right]_{i j} K=[∫01ϕi′ϕj′dx]ij, 是熟悉的全局刚度阵
- F ( t ) = [ ∫ 0 1 ϕ i ( x ) f ( x , t ) d x ] i F(t)=\left[\int_{0}^{1} \phi_{i}(x) f(x, t) d x\right]_{i} F(t)=[∫01ϕi(x)f(x,t)dx]i, 是载荷向量
然后上面的式子就是更久之前所学习的常微分方程了, 当然这个常微分方程的求解还需要初值条件:
A C ( 0 ) = F ( 0 ) A C(0)=F(0) AC(0)=F(0)
其中 F ( 0 ) = [ ∫ 0 1 ϕ i ( x ) ψ ( x ) d x ] i T F(0)=\left[\int_{0}^{1} \phi_{i}(x) \psi(x) d x\right]_{i}^{T} F(0)=[∫01ϕi(x)ψ(x)dx]iT, 是个向量.
至此, 就可以开始求解方程了.
差分格式的介入
空间的处理交给了有限元方法, 而时间可以交给差分格式, 为了使用差分格式, 直接将时间 [ 0 , T ] [0, T] [0,T] 离散为 t 0 , t 1 , ⋅ , t M t_{0}, t_{1}, \cdot, t_{M} t0,t1,⋅,tM .然后再用
向前 Euler 格式, 得到
A C k + 1 − C k Δ t + a K C k = F ( t k ) C 0 = A − 1 F 0 \begin{array}{r} A \frac{C_{k+1}-C_{k}}{\Delta t}+a K C_{k}=F\left(t_{k}\right) \\ C_{0}=A^{-1} F_{0} \end{array} AΔtCk+1−Ck+aKCk=F(tk)C0=A−1F0
或者向后 Euler 格式
A C k − C k − 1 Δ t + a K C k = F ( t k ) C 0 = A − 1 F 0 \begin{array}{r} A \frac{C_{k}-C_{k-1}}{\Delta t}+a K C_{k}=F\left(t_{k}\right) \\ C_{0}=A^{-1} F_{0} \end{array} AΔtCk−Ck−1+aKCk=F(tk)C0=A−1F0
或者二阶精度的中心 Euler 格式
A C k + 1 − C k Δ t + a K C k + C k + 1 2 = F ( t k + 1 2 ) C 0 = A − 1 F 0 \begin{array}{r} A \frac{C_{k+1}-C_{k}}{\Delta t}+a K \frac{C_{k}+C_{k+1}}{2}=F\left(t_{k+\frac{1}{2}}\right) \\ C_{0}=A^{-1} F_{0} \end{array} AΔtCk+1−Ck+aK2Ck+Ck+1=F(tk+21)C0=A−1F0
或者按需选取别的格式…
还需要处理的就是两处数值积分了 F ( t ) F(t) F(t) 和 F 0 F_{0} F0 了, 如同往常, 采用Gauss积分公式求解即可.
数值算例
考虑二维抛物方程:
{ ∂ u ( x ⃗ , t ) ∂ t − Δ u ( x ⃗ , t ) = ( 2 π 2 − 1 ) sin ( π x 1 ) sin ( π x 2 ) e − t , ( x ⃗ , t ) ∈ Ω × ( 0 , 1 ] u ( x ⃗ , t ) = sin ( π x 1 ) sin ( π x 2 ) e − t , ( x ⃗ , t ) ∈ Ω × 0 u ( x ⃗ , t ) = sin ( π x 1 ) sin ( π x 2 ) e − t , ( x ⃗ , t ) ∈ ∂ Ω × [ 0 , 1 ] \begin{cases}\frac{\partial u(\vec{x}, t)}{\partial t}-\Delta u(\vec{x}, t)=(2\pi^2-1)\sin (\pi x_1)\sin (\pi x_2) e^{-t}, & (\vec{x}, t) \in \Omega \times (0,1]\\ u(\vec{x}, t)=\sin (\pi x_1)\sin (\pi x_2) e^{-t}, & (\vec{x}, t) \in \Omega\times 0\\ u(\vec{x}, t)=\sin (\pi x_1)\sin (\pi x_2) e^{-t}, & (\vec{x}, t) \in \partial \Omega\times[0,1]\end{cases} ⎩⎪⎨⎪⎧∂t∂u(x,t)−Δu(x,t)=(2π2−1)sin(πx1)sin(πx2)e−t,u(x,t)=sin(πx1)sin(πx2)e−t,u(x,t)=sin(πx1)sin(πx2)e−t,(x,t)∈Ω×(0,1](x,t)∈Ω×0(x,t)∈∂Ω×[0,1]
其中, 空间区域 Ω : = [ 0 , 1 ] × [ 0 , 1 ] \Omega:=[0,1]\times[0,1] Ω:=[0,1]×[0,1], 其真实解为 u ( x ⃗ , t ) = sin ( π x 1 ) sin ( π x 2 ) e − t u(\vec{x}, t)=\sin (\pi x_1)\sin (\pi x_2) e^{-t} u(x,t)=sin(πx1)sin(πx2)e−t .
下面演示基于 FEALPy 求解这个算例的过程.
from fealpy.pde.parabolic_model_2d import SinSinExpData
from fealpy.mesh import MeshFactory as MF
from fealpy.functionspace import LagrangeFiniteElementSpace
from fealpy.boundarycondition import DirichletBC
from fealpy.decorator import cartesian
from scipy.sparse.linalg import spsolve
import matplotlib.pyplot as plt
t_list = []
error = []
# 创建 PDE 模型
pde = SinSinExpData()
# 创建网格
domain = [0, 1, 0, 1]
mesh = MF.boxmesh2d(domain, nx=5, ny=5, meshtype='tri')
# 时间离散
timeline = pde.time_mesh(0, 1, 100)
# 建立 Lagrange 有限元函数空间
space = LagrangeFiniteElementSpace(mesh, p=2)
# 时间步进求解
for i in range(100):
t = timeline.next_time_level()
# 创建 Dirichlet 边界条件对象
@cartesian
def dirichlet(p):
return pde.dirichlet(p, t)
bc = DirichletBC(space, dirichlet)
# 创建离散代数系统
uh = space.function()
A = space.stiff_matrix()
@cartesian
def source(p):
return pde.source(p, t)
F = space.source_vector(source)
# 处理边界条件
A, F = bc.apply(A, F, uh)
# 求解离散代数系统
uh[:] = spsolve(A, F)
# 计算 L2 误差并保存
@cartesian
def solution(p):
return pde.solution(p, t)
L2Error = space.integralalg.L2_error(solution, uh)
# print('t:/t', t, '/tL2Error:', L2Error)
t_list.append(t)
error.append(L2Error)
# 前进一层
timeline.forward()
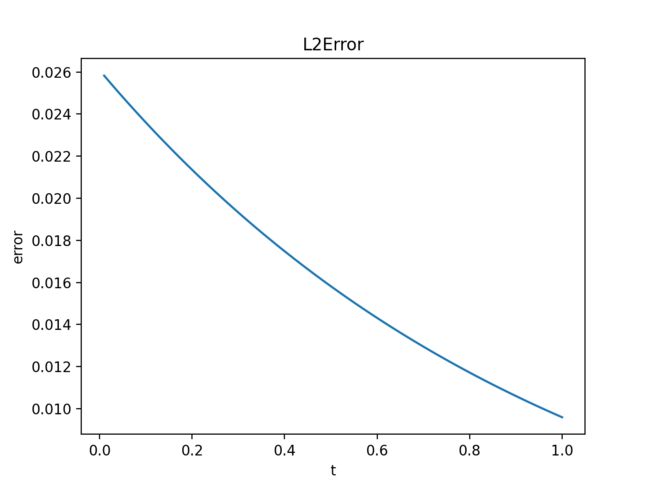
# 绘制时间方向 L2 误差
plt.xlabel('t')
plt.ylabel('error')
plt.title('L2Error')
plt.plot(t_list, error)
plt.show()
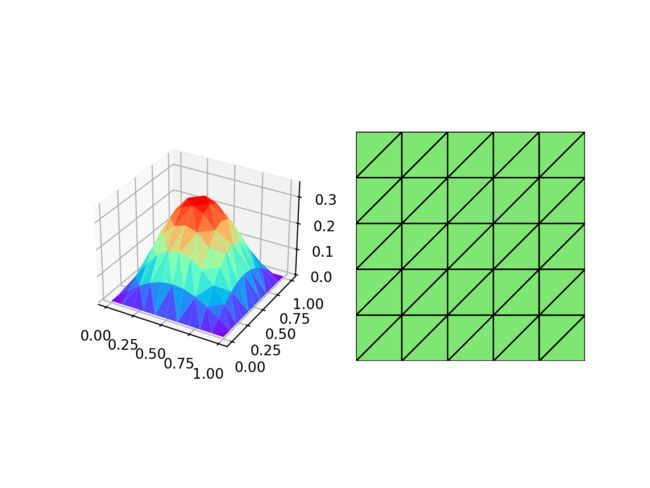
# 绘制数值解图像和网格图像
fig = plt.figure()
axes = fig.add_subplot(1, 2, 1, projection='3d')
uh.add_plot(axes, cmap='rainbow')
axes = fig.add_subplot(1, 2, 2)
mesh.add_plot(axes)
plt.show()
本人水平有限, 若有错误, 欢迎联系批评指正
作者邮箱: [email protected]