机器学习笔记1-逻辑回归
机器学习笔记1-逻辑回归
- 入门示例
-
- 1. 模型训练
- 2. 数据和模型可视化
- 3. 预测新样本
- 算法实战
-
- 1. 数据的导入和查看
- 2. 利用逻辑回归模型在二分类上进行训练和预测
- 3. 利用逻辑回归模型在三分类(多分类)上进行训练和预测
- 逻辑回归模型原理
入门示例
1. 模型训练
- 导入包
numpy:基础函数库
matplotlib.pyplot:画图库
seaborn:高阶画图库
LogisticRegression:逻辑回归模型函数
## 基础函数库
import numpy as np
## 导入画图库
import matplotlib.pyplot as plt
import seaborn as sns
## 导入逻辑回归模型函数
from sklearn.linear_model import LogisticRegression
- 模型训练:
- 创建模型:
模型名 = LogisticRegression - 训练模型:
模型名.fit(特征值数据集, 标签值数据集)
##Demo演示LogisticRegression分类
## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])
## 创建逻辑回归模型
lr_clf = LogisticRegression()
## 用数据集训练逻辑回归模型,得到参数
lr_clf = lr_clf.fit(x_fearures, y_label)
- 模型参数查看
- 查看系数:
模型名.coef_,模型名.intercept_
## 查看其对应模型的w
print('the weight of Logistic Regression:',lr_clf.coef_)
## 查看其对应模型的w0
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)
2. 数据和模型可视化
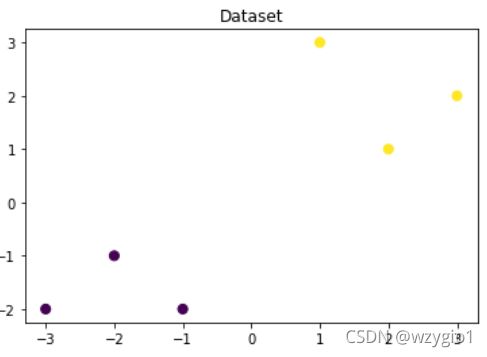
- 可视化构造的数据样本点
## 可视化构造的数据样本点
# c:根据y_label创建颜色数组,s:点大小
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()
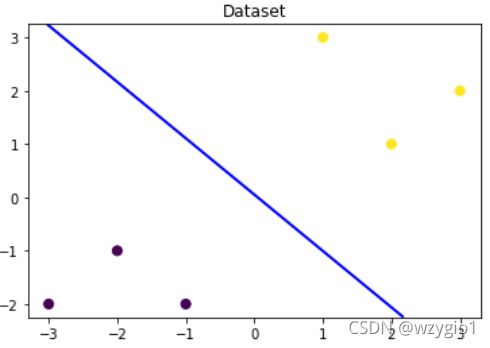
- 设定精确度:确定全图的点数
- 构造坐标矩阵:先通过精确度构造数组,再通过数组构造坐标矩阵
- 使用模型进行预测:每个坐标点对应两个概率,一个是属于0的概率,一个是属于1的概率
- 作图:只取每个坐标点的第一个概率,将概率为0.5的点连线生成决策边界。
# 可视化决策边界
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
# 设定精确度
nx, ny = 200, 100
# 从plt获取x轴和y轴范围。
x_min, x_max = plt.xlim()
y_min, y_max = plt.ylim()
# np.linespace:构造数组
# np.meshgrid:通过数组构造矩阵,分别是全图两万个点的横坐标和纵坐标
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))
# 用构造好的模型预测
# np.c_:将两个一维数组凑成一个二维数组,对应元素成对,相当于每个点的坐标
z_proba = lr_clf.predict_proba(np.c_[x_grid.ravel(), y_grid.ravel()])
# 只取第一个概率,并使概率矩阵中的每个元素对应每个坐标点
z_proba = z_proba[:, 1].reshape(x_grid.shape)
# contour:连线z_proba为0.5的坐标点
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')
plt.show()
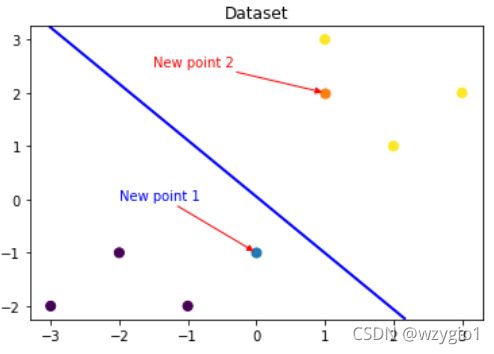
3. 预测新样本
- 在图上标注出两个新样本点
### 可视化预测新样本
plt.figure()
## new point 1
x_fearures_new1 = np.array([[0, -1]])
# 在散点图上标注出该点
plt.scatter(x_fearures_new1[:,0],x_fearures_new1[:,1], s=50, cmap='viridis')
# 设置标注样式:字体样式,箭头样式
plt.annotate(s='New point 1',xy=(0,-1),xytext=(-2,0),color='blue',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
## new point 2
x_fearures_new2 = np.array([[1, 2]])
plt.scatter(x_fearures_new2[:,0],x_fearures_new2[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 2',xy=(1,2),xytext=(-1.5,2.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
## 训练样本
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
# 可视化决策边界
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')
plt.show()
- 使用模型预测两个新样本点的标签
## 在训练集和测试集上分别利用训练好的模型进行预测
y_label_new1_predict = lr_clf.predict(x_fearures_new1)
y_label_new2_predict = lr_clf.predict(x_fearures_new2)
print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)
## 由于逻辑回归模型是概率预测模型(前文介绍的 p = p(y=1|x,\theta)),所以我们可以利用 predict_proba 函数预测其概率
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)
print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)
算法实战
基于鸢尾花(iris)数据集的逻辑回归分类实践。这是一个sklearn中自带的实例
1. 数据的导入和查看
- 库函数导入
## 基础函数库
import numpy as np
import pandas as pd
## 绘图函数库
import matplotlib.pyplot as plt
import seaborn as sns
- 数据读取/载入
load_iris是一个下载并得到数据集的func;help(func)可以直接查询该函数的信息。
数据集.target:得到标签集数据集.data:得到特征集
## 我们利用 sklearn 中自带的 iris 数据作为数据载入,并利用Pandas转化为DataFrame格式
from sklearn.datasets import load_iris
data = load_iris() # 得到数据集。data是sklearn.utils.Bunch类型。
iris_target = data.target # 得到数据对应的标签
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) # 利用Pandas转化为DataFrame格式
- 表格(DataFrame)数据查看
.info(),.head(),.tail(),.describe()
## 利用.info()查看数据的整体信息
iris_features.info()
## 进行简单的数据查看,我们可以利用 .head() 头部.tail()尾部
iris_features.head()
iris_features.tail()
## 利用value_counts函数查看每个类别数量
pd.Series(iris_target).value_counts()
## 对于特征进行一些统计描述
iris_features.describe()
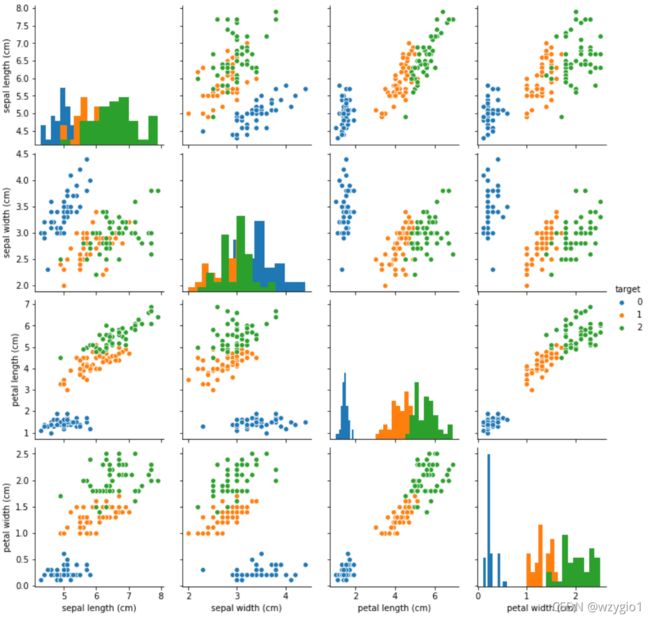
- 可视化数据
sns.pariplot:两两特征生成的散点图(一共四个特征)。
## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝,防止对于原始数据的修改
iris_all['target'] = iris_target
## 特征组合对应标签的散点可视化:diag_kind-对角线图样式,hue-根据什么数据展现不同的颜色
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()
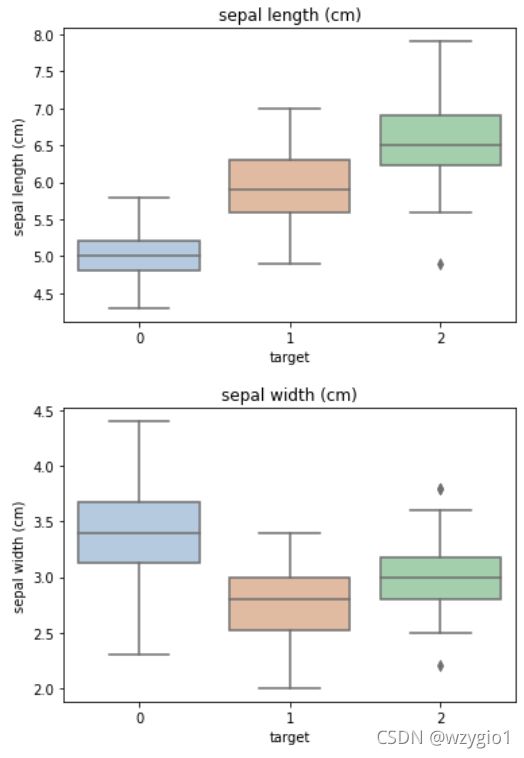
sns.boxplot:每种特征值相对于标签的分布情况。
# x和y都是列名,col是列名;saturation是饱和度
for col in iris_features.columns:
sns.boxplot(x='target', y=col, saturation=0.5,palette='pastel', data=iris_all)
plt.title(col)
plt.show()
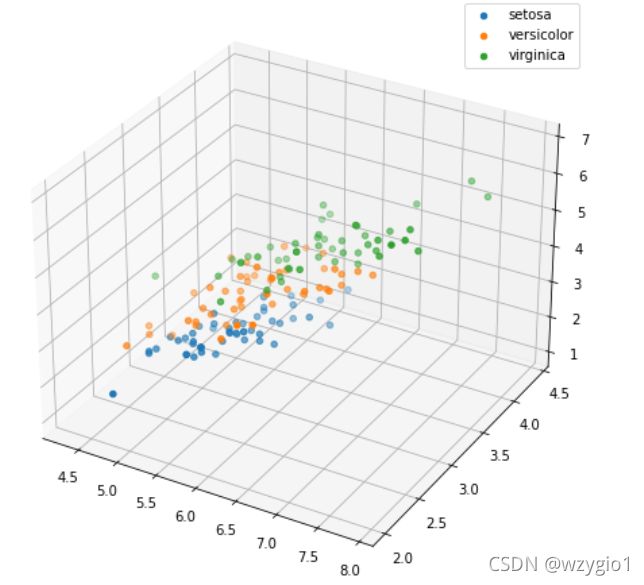
- 创建三维散点图
a x = f i g . a d d _ s u b p l o t ( ) ax = fig.add\_subplot() ax=fig.add_subplot():设定坐标样式
ax.scatter:画出散点图
# 选取其前三个特征绘制三维散点图
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10,8))
# 创建坐标样式
ax = fig.add_subplot(111, projection='3d')
# 根据target将数据集分类
iris_all_class0 = iris_all[iris_all['target']==0].values
iris_all_class1 = iris_all[iris_all['target']==1].values
iris_all_class2 = iris_all[iris_all['target']==2].values
# 'setosa'(0), 'versicolor'(1), 'virginica'(2)
ax.scatter(iris_all_class0[:,0], iris_all_class0[:,1], iris_all_class0[:,2],label='setosa')
ax.scatter(iris_all_class1[:,0], iris_all_class1[:,1], iris_all_class1[:,2],label='versicolor')
ax.scatter(iris_all_class2[:,0], iris_all_class2[:,1], iris_all_class2[:,2],label='virginica')
plt.legend()
plt.show()
2. 利用逻辑回归模型在二分类上进行训练和预测
- 数据预处理:
.iloc[]:切片train_test_split():分割数据集
## 为了正确评估模型性能,将数据划分为训练集和测试集,并在训练集上训练模型,在测试集上验证模型性能。
from sklearn.model_selection import train_test_split
from sklearn import metrics
## 选择其类别为0和1的样本 (不包括类别为2的样本):一共150个样本,每类50个样本,0和1的样本即前一百个
iris_features_part = iris_features.iloc[:100]
iris_target_part = iris_target[:100]
# train_test_split就是一个切片工具;其实自己切片也行,但是打乱数据不容易实现
## 测试集大小为20%, 80%/20%分
x_train, x_test, y_train, y_test = train_test_split(iris_features_part, iris_target_part, test_size = 0.2, random_state = 2020)
- 训练模型
## 从sklearn中导入逻辑回归模型
from sklearn.linear_model import LogisticRegression
## 定义 逻辑回归模型
clf = LogisticRegression(random_state=0, solver='lbfgs')
# 在训练集上训练逻辑回归模型
clf.fit(x_train, y_train)
## 查看其对应的w
print('the weight of Logistic Regression:',clf.coef_)
## 查看其对应的w0
print('the intercept(w0) of Logistic Regression:',clf.intercept_)
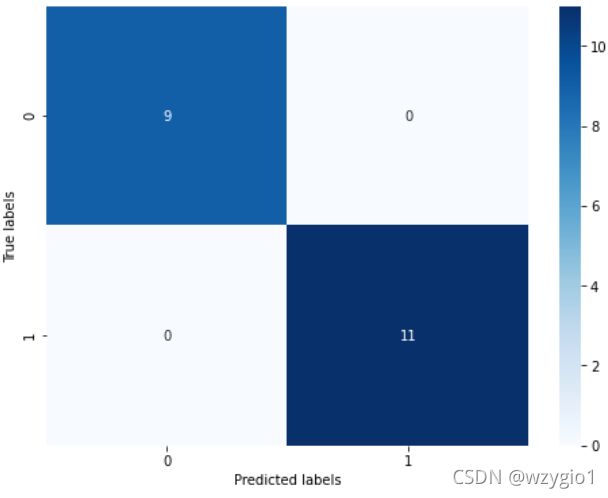
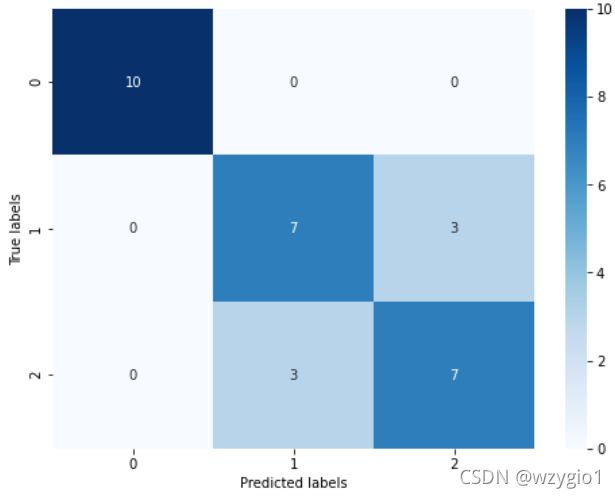
- 使用模型预测并可视化结果:构建混淆矩阵并根据其做出热力图
- 预测-
模型名.predict(特征集) - 混淆矩阵-
metrics.confusion_matrix(预测值,真实值):预测值和真实值各类情况统计矩阵 - 热力图-
sns.heatmap(混淆矩阵名, annot=True, cmap='Blues'):可视化分布情况,某一处分布的值越多则颜色越深。
## 在训练集和测试集上分布利用训练好的模型进行预测
# 尽管模型是由训练集训练得到,但是用模型去预测训练集的标签时,预测值和实际值也会有误差
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)
## 利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
# metrics.accuracy_score: 对比两个数组,输出其相同的元素所占的比例
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
## 查看混淆矩阵 (预测值和真实值的各类情况统计矩阵)
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
3. 利用逻辑回归模型在三分类(多分类)上进行训练和预测
- 数据预处理
## 测试集大小为20%, 80%/20%分
x_train, x_test, y_train, y_test = train_test_split(iris_features, iris_target, test_size = 0.2, random_state = 2020)
- 模型训练
## 定义 逻辑回归模型
clf = LogisticRegression(random_state=0, solver='lbfgs')
# 在训练集上训练逻辑回归模型
# 自动三分类,不用一对余
clf.fit(x_train, y_train)
## 查看其对应的w
print('the weight of Logistic Regression:\n',clf.coef_)
## 查看其对应的w0
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)
## 由于这个是3分类,所有我们这里得到了三个逻辑回归模型的参数,其三个逻辑回归组合起来即可实现三分类。
- 使用模型预测并可视化结果:构建混淆矩阵并根据其做出热力图
## 在训练集和测试集上分布利用训练好的模型进行预测
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)
## 由于逻辑回归模型是概率预测模型(前文介绍的 p = p(y=1|x,\theta)),所有我们可以利用 predict_proba 函数预测其概率
train_predict_proba = clf.predict_proba(x_train)
test_predict_proba = clf.predict_proba(x_test)
print('The test predict Probability of each class:\n',test_predict_proba[:10,:])
## 其中第一列代表预测为0类的概率,第二列代表预测为1类的概率,第三列代表预测为2类的概率。
## 利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
## 查看混淆矩阵
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
逻辑回归模型原理
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
l o g i ( z ) = 1 1 + e − z logi(z)=\frac{1}{1+e^{-z}} logi(z)=1+e−z1
其对应的函数图像可以表示如下:
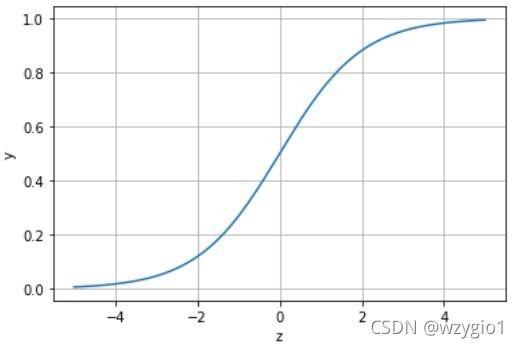
通过上图我们可以发现 Logistic 函数是单调递增函数,并且在z=0的时候取值为0.5,并且 l o g i ( ⋅ ) logi(\cdot) logi(⋅)函数的取值范围为 ( 0 , 1 ) (0,1) (0,1)。
而回归的基本方程为 z = w 0 + ∑ i N w i x i z=w_0+\sum_i^N w_ix_i z=w0+∑iNwixi,
将回归方程写入其中为:
p = p ( y = 1 ∣ x , θ ) = h θ ( x , θ ) = 1 1 + e − ( w 0 + ∑ i N w i x i ) p = p(y=1|x,\theta) = h_\theta(x,\theta)=\frac{1}{1+e^{-(w_0+\sum_i^N w_ix_i)}} p=p(y=1∣x,θ)=hθ(x,θ)=1+e−(w0+∑iNwixi)1
所以, p ( y = 1 ∣ x , θ ) = h θ ( x , θ ) p(y=1|x,\theta) = h_\theta(x,\theta) p(y=1∣x,θ)=hθ(x,θ), p ( y = 0 ∣ x , θ ) = 1 − h θ ( x , θ ) p(y=0|x,\theta) = 1-h_\theta(x,\theta) p(y=0∣x,θ)=1−hθ(x,θ)
逻辑回归从其原理上来说,逻辑回归其实是实现了一个决策边界:对于函数 y = 1 1 + e − z y=\frac{1}{1+e^{-z}} y=1+e−z1,当 z = > 0 z=>0 z=>0时, y = > 0.5 y=>0.5 y=>0.5,分类为1,当 z < 0 z<0 z<0时, y < 0.5 y<0.5 y<0.5,分类为0,其对应的 y y y值我们可以视为类别1的概率预测值.
对于模型的训练而言:实质上来说就是利用数据求解出对应的模型的特定的 w w w。从而得到一个针对于当前数据的特征逻辑回归模型。
而对于多分类而言,将多个二分类的逻辑回归组合,即可实现多分类。
材料参考自阿里天池机器学习训练营