线性分类（三）-- 逻辑回归 LR

        逻辑回归（Logistic Regression）也被称作对数几率回归，是一种用于解决二分类（0 or 1）问题的机器学习方法，用于估计某种事物的可能性。比如某用户购买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。 注意，这里用的是“可能性”，而非数学上的“概率”，logisitc回归的结果并非数学定义中的概率值，不可以直接当做概率值来用。该结果往往用于和其他特征值加权求和，而非直接相乘。

        逻辑回归与线性回归是什么关系呢？
        逻辑回归（Logistic Regression）与线性回归（Linear Regression）都是一种广义线性模型（generalized linear model）。逻辑回归假设因变量 $y$ 服从伯努利分布，而线性回归假设因变量 $y$ 服从高斯分布。 因此与线性回归有很多相同之处，去除Sigmoid激活函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

        为什么要使用逻辑回归而是直接使用线性回归模型呢？
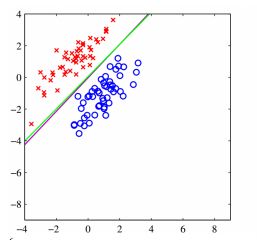
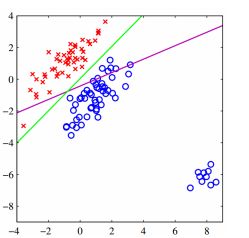
        对于下图，紫色线表示线性回归模型，绿色线表示逻辑回归模型，对比两幅图，我们可以看到，在角落加上一块蓝色点之后，线性回归的线会向下倾斜，但是逻辑回归分类的还是很准确，逻辑回归在解决分类问题上还是不错的。

---

1 数学基础

1.1 logistic distribution

        设 $X$ 是连续随机变量，$X$ 服从逻辑斯谛分布，则具有下列分布函数：
$$F(x)=P(X⩽x)=\frac{1}{1+\exp (-(x-\mu )/\gamma )}\text{\hspace{1em}(1-1)}$$
        式中，$\mu$ 为位置参数，$\gamma >0$ 为形状参数。

1.2 Sigmoid Function

        Sigmoid函数是一个常用的逻辑函数（logistic function），形式如下：
$$y=\frac{1}{1+e^{-z}}$$
        这个函数把实数域映射到 $(0,1)$ 区间，这个范围正好是概率的范围， 而且可导，对于0输入， 得到的是0.5，可以用来表示等可能性。其函数曲线如下：

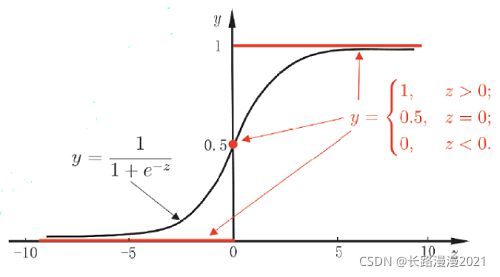
        从上图可以看到sigmoid函数是一个s形的曲线，它的取值在 $[0,1]$ 之间。

---

2 数学模型

2.1 二项逻辑斯谛回归模型

        事件的几率（odds），是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是 $p$，那么该事件的几率是 $o=p/(1-p)$。取该事件发生几率的对数，定义为该事件的对数几率（log odds）或logit函数：
$$logit(p)=log(o)=\log \frac{p}{1-p}\text{\hspace{1em}(2-1)}$$
        几率和概率之间的关系有这样一种表达
$$o=\frac{p}{1-p}，p=\frac{o}{1-o}\text{\hspace{1em}(2-2)}$$

        取对数的理解大概是这样：事件发生的概率 $p$ 的取值范围为 $[0,1]$，对于这样的输入，计算出来的几率只能是非负的，而通过取对数，便可以将输出转换到整个实数范围内。

        假设数据集如下：
$$Data：\{(x_i\text{xi}{x}_i,y_i){\}}_{i=1}^N{x}_i\text{xi}{x}_i\in {\mathbb{R}}^p{y}_i\in \{0,1\}\text{\hspace{1em}(2-3)}$$
        这样，我们就可以将对数几率记为输入特征值的线性表达式 ：
$$logit(P(Y=1|x\text{x}x))=w_0+w_1{x}_1+\dots +w_p{x}_p=\sum _{i=0}^p{w}_i{x}_i={w\text{w}w}^{T}x\text{x}x\text{\hspace{1em}(2-4)}$$

        这里为了简单起见，$x\text{x}x=\left[\begin{array}{cccc}1& x_1& \cdots & x_p\end{array}\right]$ 和 $w\text{w}w=\left[\begin{array}{cccc}{w}_0& w_1& \cdots & w_p\end{array}\right]$ 分别为 $p+1$ 维的增广特征向量和增广权重向量。
        其中，$P(Y=1|x\text{x}x)$ 是条件概率分布，表示当输入为 $x\text{x}x$ 时，实例被分为1类的概率，依据此概率我们能得到事件发生的对数几率。但是，我们的初衷是做分类器，简单点说就是通过输入特征来判定该实例属于哪一类别或者属于某一类别的概率。所以我们取logit函数的反函数，令 ${w\text{w}w}^{T}x\text{x}x$ 的线性组合为输入，$p$ 为输出，经如下推导
$$\begin{gathered} logit(P(Y=1|x\text{x}x))=\log \frac{P(Y=1|x\text{x}x)}{1-P(Y=1|x\text{x}x)}={w\text{w}w}^{T}x\text{x}x \\ \Rightarrow P(Y=1|x\text{x}x)=\frac{exp({w\text{w}w}^{T}x\text{x}x)}{1+exp({w\text{w}w}^{T}x\text{x}x)} \\ \Rightarrow P(Y=0|x\text{x}x)=1-P(Y=1|x\text{x}x)=\frac{1}{1+exp({w\text{w}w}^{T}x\text{x}x)}\text{\hspace{1em}(2-5)} \end{gathered}$$

        对于上面的公式，可以这样理解：为了实现逻辑回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和带入sigmoid函数中，进而得到一个范围在0-1之间的数值，最后设定一个阈值，在大于阈值时判定为1，否则判定为0。以上便是逻辑斯谛回归算法是思想，公式就是分类器的函数形式。

        假设 $w\text{w}w$ 的极大似然估计值为 $\hat{w}\text{w^}\hat{w}$ ，那么学到的Logistic Regression模型为：

$$\begin{gathered} P(y=1|x\text{x}x)=\frac{1}{1+e^{-{\hat{\mathbf{w}}}^T\mathbf{x}}} \\ P(y=0|\mathbf{x})=\frac{e^{-{\hat{\mathbf{w}}}^T\mathbf{x}}}{1+e^{-{\hat{\mathbf{w}}}^T\mathbf{x}}}\text{\hspace{1em}(2-12)} \end{gathered}$$

2.2 参数估计

        上一节已经确定了Logistic分类模型，但权重 $w\text{w}w$（回归系数）是不确定的，所以需要求得最佳的回归系数，从而使得分类器尽可能的精确。

        下面我们使用最优化方法来获得最佳的回归系数，在很多分类器中，都会将预测值与实际值的误差的平方和作为损失函数（代价函数），通过梯度下降算法求得函数的最小值来确定最佳系数。前面我们提到过某件事情发生的概率为 $p$，在逻辑回归中所定义的损失函数就是定义一个似然函数做概率的连乘，数值越大越好，也就是某个样本属于其真实标记样本的概率越大越好。如，一个样本的特征 $x\text{x}x$ 所对应的标记为1，通过逻辑斯蒂回归模型之后，会给出该样本的标记为1和为-1的概率分别是多少，我们当然希望模型给出该样本属于1的概率越大越好。既然是求最大值，那我们用到的最优化算法就是梯度上升，其实也就是与梯度下降相反而已。

2.2.1 交叉熵损失函数

        下面为了方便求解，令 $p_1=P(Y=1|x\text{x}x)，p_0=P(Y=0|x\text{x}x)$，由于 $Y$ 服从伯努利分布，则
$$p=P((Y=y)|x\text{x}x;w\text{w}w)=p_1^y\cdot p_0^{1-y}，y\in \{0,1\}\text{\hspace{1em}(2-6)}$$

        假定数据集中的每个样本都是独立的，定义一个最大似然函数 $L$，如下
$$L(w\text{w}w)=P(Y|X;w\text{w}w)=\prod _{i=1}^{N}P(y_i|{\mathbf{x}}_i;w\text{w}w)$$

        取似然函数的对数，
$$\begin{array}{rl}J(w\text{w}w)=ln(L(w\text{w}w))& =ln\prod _{i=1}^{N}P(y_i|{\mathbf{x}}_i)\\ & =\sum _{i=1}^{N}lnP(y_i|{\mathbf{x}}_i)\\ & =\underset{-crossentropy}{\sum _{i=1}^N(y_{i}ln{p}_1+(1-y_i)ln{p}_0)}\end{array}\text{\hspace{1em}(2-7)}$$

        在进行极大似然估计的时候我们都知道要取对数，那为什么我们要取对数呢？
        首先，在似然函数值非常小的时候，可能出现数值溢出的情况（简单点说就是数值在极小的时候因为无限趋近于0而默认其等于0，具体可以参考：数值溢出），使用对数函数降低了这种情况发生的可能性。其次，我们可以将各因子的连乘转换为和的形式，利用微积分中的方法，通过加法转换技巧可以更容易地对函数求导。

        这里似然函数是取最大值的，我们可以直接将其确定为损失函数然后使用梯度上升算法求最优的回归系数。
$$MLE(max)\Rightarrow LossFunction(min-CrossEntropy)\text{\hspace{1em}(2-8)}$$
        从优化的角度考虑，可以对 $L(w\text{w}w)$ 取负，作为损失函数，这样就可以使用我们熟悉的梯度下降算法进行求解。

        均方差和交叉熵损失的区别：均方差注重每个分类的结果，而交叉熵只注重分类正确的结果，所以交叉熵适合于分类问题，而不适合于回归问题，但是 logistic回归其实本质是 0-1 分类问题，所以这里适合作为 logistic 回归的损失函数。

2.2 梯度上升法估计参数

        对 $J(w)$ 求梯度，其中 $p_1^{{}^{\prime }}=p_1(1-p_1)$

$$\begin{array}{rl}\nabla \ln L(\mathbf{w})=\frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}& =\sum _{i=1}^N(y_i\frac{1}{p_1}{p}_1(1-p_1){\mathbf{x}}_i+(1-y_i)\frac{1}{1-p_1}(-1)p_1(1-p_1){\mathbf{x}}_i)\\ & =\sum _{i=1}^N(y_i(1-p_1){\mathbf{x}}_i-(1-y_i)p_1{\mathbf{x}}_i)\\ & =\sum _{i=1}^N(y_i{\mathbf{x}}_i-p_1{\mathbf{x}}_i)\\ & =\sum _{i=1}^N(y_i-p_1){\mathbf{x}}_i\end{array}\text{\hspace{1em}(2-9)}$$

        令 $\frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}=0$，由于概率的非线性，此式无法直接求解，因此在实际训练中，采用梯度上升或拟牛顿法来求 $J(\mathbf{w})$ 的极大值点。
        我们使用梯度上升法(Gradient ascent method)求解参数 $\mathbf{w}$，其迭代公式为
$$\mathbf{w}=\mathbf{w}+\alpha \nabla \ln L(\mathbf{w})\text{\hspace{1em}(2-10)}$$

        定义 $E\text{E}E=Y-{p\text{p}p}_1$，则可以得到
$$\mathbf{w}=\mathbf{w}+\alpha \sum _{i=1}^N(y_i-p_1){\mathbf{x}}_i=\mathbf{w}+\alpha {X\text{X}X}^{T}E\text{E}E\text{\hspace{1em}(2-11)}$$

代码实现

from numpy import *
import numpy as np
import matplotlib.pyplot as plt
import matplotlib


# Load data from file: Feature-dataMat，Label-labelMat
def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('D:\\2021\\python-code\\Logistic\\testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat

# sigmoid Function
def sigmoid(inX):
    return 1.0/(1+exp(-inX))

# graAscent function implements the gradient ascent method
# Gradient Ascent Algorithm, each parameter iteration needs to traverse the entire data set
def gradAscent(dataMatrix, classLabels):
    dataMatrix = mat(dataMatrix)             # convert to NumPy matrix
    labelMat = mat(classLabels).transpose()  # convert to NumPy matrix
    m, n = shape(dataMatrix)
    alpha = 0.01
    maxCycles = 500
    weights = ones((n, 1))
    weights_list = list()
    for k in range(maxCycles):               # heavy on matrix operations
        h = sigmoid(dataMatrix*weights)      # matrix mult
        error = (labelMat - h)               # vector subtraction
        weights = weights + alpha * dataMatrix.transpose() * error  # matrix mult
        weights_list.append(weights)
    return weights, weights_list                                            


# Draw weighted image
def plot_weights(weights_list):
    fig = plt.figure(figsize=(8, 8))
    x = range(len(weights_list))
    w0 = [item[0, 0] for item in weights_list]
    w1 = [item[1, 0] for item in weights_list]
    w2 = [item[2, 0] for item in weights_list]

    # Set matplotlib to display Chinese and negative signs normally
    matplotlib.rcParams['font.sans-serif']=['SimHei']   # 用黑体显示中文
    matplotlib.rcParams['axes.unicode_minus']=False     # 正常显示负号
    plt.subplot(311)
    plt.plot(x, w0, 'r-', label="w0")
    plt.ylabel("w0")
    plt.subplot(312)
    plt.plot(x, w1, 'g-', label="w1")
    plt.ylabel("w1")
    plt.subplot(313)
    plt.plot(x, w2, 'b-', label="w2")
    plt.xlabel("迭代次数")
    plt.ylabel("w2")
    plt.show()

# Draw classification results
def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1])
            ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1])
            ycord2.append(dataArr[i, 2])
    fig = plt.figure(figsize=(6, 4))
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y.transpose())
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

# Draw sigmod function image
def plot_sigmoid():
    x = arange(-60.0, 60.0, 1)
    y = sigmoid(x)
    fig = plt.figure(figsize=(8, 4))
    plt.xlabel('x')
    plt.ylabel('sigmoid(x)')
    plt.plot(x, y.transpose())
    plt.show()


if __name__ == "__main__":
    data_mat, label_mat = loadDataSet()
    weights, weights_list = gradAscent(data_mat, label_mat)
    plot_weights(weights_list)
    plotBestFit(weights)
    plot_sigmoid()

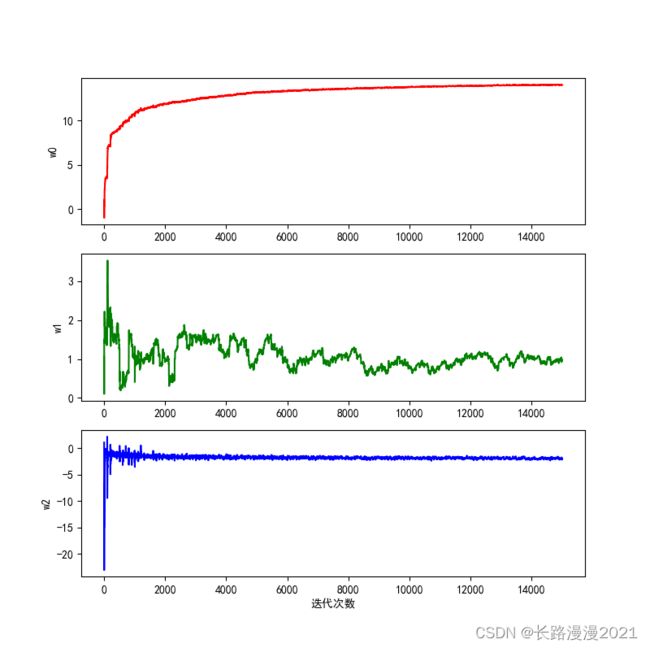
        使用梯度上升法获得的分类结果如下图所示

        迭代次数与最终参数的变化如下图所示：

2.2 改进的随机梯度上升法

        梯度上升算法在每次更新回归系数(最优参数)时，都需要遍历整个数据集。假设，我们使用的数据集一共有100个样本，回归参数有 3 个，那么dataMatrix就是一个100×3的矩阵。每次计算 $h$ 的时候，都要计算dataMatrix×weights这个矩阵乘法运算，要进行100×3次乘法运算和100×2次加法运算。同理，更新回归系数(最优参数)weights时，也需要用到整个数据集，要进行矩阵乘法运算。总而言之，该方法处理100个左右的数据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。因此，需要对算法进行改进，我们每次更新回归系数(最优参数)的时候，能不能不用所有样本呢？一次只用一个样本点去更新回归系数(最优参数)？这样就可以有效减少计算量了，这种方法就叫做随机梯度上升算法(Stochastic gradient ascent)。

# 改进后的随机梯度上升算法
# 从两个方面对随机梯度上升算法进行了改进，正确率确实提高了很多
# 改进一：对于学习率alpha采用非线性下降的方式使得每次都不一样
# 改进二：每次使用一个数据，但是每次随机的选取数据，选过的不在进行选择
# numIter 这个迭代次数对于分类效果影响很大，很小时分类效果很差
def stocGradAscent(dataMatrix, classLabels, numIter=150):
    dataMatrix = mat(dataMatrix)
    labelMat = mat(classLabels).transpose()
    m,n = np.shape(dataMatrix)                                                
    weights = np.ones((n,1))  
    weights_list = list()                                                    
    for j in range(numIter):                                           
        dataIndex = list(range(m))
        for i in range(m):           
            alpha = 4/(1.0+j+i)+0.01            
            randIndex = int(random.uniform(0,len(dataIndex)))              
            h = sigmoid(sum(dataMatrix[randIndex]*weights))                   
            error = classLabels[randIndex] - h                               
            weights = weights + alpha * dataMatrix[randIndex].transpose() * error 
            del(dataIndex[randIndex])  
            weights_list.append(weights)                                      
    return weights, weights_list 

        该算法第一个改进之处在于，alpha在每次迭代的时候都会调整，并且，虽然alpha会随着迭代次数不断减小，但永远不会减小到0，因为这里还存在一个常数项。必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响。如果需要处理的问题是动态变化的，那么可以适当加大上述常数项，来确保新的值获得更大的回归系数。另一点值得注意的是，在降低alpha的函数中，alpha每次减少 $1/(j+i)$，其中 $j$ 是迭代次数，$i$ 是样本点的下标。第二个改进的地方在于跟新回归系数(最优参数)时，只使用一个样本点，并且选择的样本点是随机的，每次迭代不使用已经用过的样本点。这样的方法，就有效地减少了计算量，并保证了回归效果。

        使用随机梯度上升法获得的分类结果如下图所示

        迭代次数与最终参数的变化如下图所示，可以看到，在 80 次以后，各参数基本趋于稳定，这个过程大约迭代了整个矩阵 80次，相比较于原先的 300 多次，大幅减小了迭代周期。

2.3 sklearn实现

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
import pandas as pd
import math
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

# 导入数据
dataMat = []
labelMat = []
fr = open('D:\\2021\\python-code\\Logistic\\testSet.txt')
for line in fr.readlines():
    lineArr = line.strip().split()
    dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
    labelMat.append(int(lineArr[2]))

dataMat_train, dataMat_test, labelMat_train, labelMat_test = train_test_split(dataMat,labelMat,test_size = 0.3)
model_logistic_regression = linear_model.LogisticRegression()
model_logistic_regression.fit(dataMatrix, classLabels)

# 训练数据的准确率和测试数据的准确率
train_score = model_logistic_regression.score(dataMat_train,labelMat_train)
test_score = model_logistic_regression.score(dataMat_test,labelMat_test)

# 回归系数
print(model_logistic_regression.coef_)
# 截距
print(model_logistic_regression.intercept_)
print('\ntrain score:{}'.format(train_score))
print('test score:{}'.format(test_score))

输出结果:
 	train score:0.9857142857142858
	test score:0.9
	[[ 2.15916228  0.62565256 -0.6774892 ]]
	[2.15916228]

---

小结

        logistic回归是一种二分类算法，它用Logistic函数预测出一个样本属于正样本的概率值。预测时，并不需要真的用Logistic函数映射，而只需计算一个线性函数，因此是一种线性模型。训练时，采用了最大似然估计，优化的目标函数是一个凸函数，因此能保证收敛到全局最优解。虽然有概率值，但Logistic回归是一种判别模型而不是生成模型，因为它并没有假设样本向量 $x\text{x}x$ 所服从的概率分布，即没有对 $p(x\text{x}x,y)$ 建模，而是直接预测类后验概率 $p(y|x\text{x}x)$ 的值。

1. 优缺点
        Logistic回归是一种被人们广泛使用的算法，因为它非常高效，不需要太大的计算量，又通俗易懂，不需要缩放输入特征，不需要任何调整，且很容易调整，并且输出校准好的预测概率。

        与线性回归一样，当去掉与输出变量无关的属性以及相似度高的属性时，Logistic回归效果确实会更好。因此特征处理在Logistic和线性回归的性能方面起着重要的作用。

        Logistic回归的另一个优点是它非常容易实现，且训练起来很高效。在研究中，通常以 Logistic 回归模型作为基准，再尝试使用更复杂的算法。

        由于其简单且可快速实现的原因，Logistic回归也是一个很好的基准，你可以用它来衡量其他更复杂的算法的性能。

        它的一个缺点就是我们不能用Logistic回归来解决非线性问题，因为它的决策边界是线性的。

2. 推广到多类
        logistic回归只能用于二分类问题，将它进行推广可以得到处理多类分类问题的softmax回归，思路类似，采用指数函数进行变换，然后做归一化。这种变换在神经网络尤其是深度学习中被广为使用，对于多分类问题，神经网络的最后一层往往是softmax层（不考虑损失函数层，它只在训练时使用）。对于决策边界和softmax回归的介绍，请看下一篇！

---

参考

• 逻辑斯谛回归之决策边界 logistic regression – decision boundary：https://blog.csdn.net/u012328159/article/details/51068427
• 逻辑回归（Logistic Regression）：https://zhuanlan.zhihu.com/p/28408516
• logistic回归详解：https://blog.csdn.net/tian_tian_hero/article/details/89409472
• logistic回归介绍以及原理分析：https://www.cnblogs.com/xiuercui/p/11945567.html
• logistic回归原理与实现：https://zhuanlan.zhihu.com/p/95132284
• logistic回归原理解析及Python应用实例：https://blog.csdn.net/feilong_csdn/article/details/64128443
• 理解 logistic 回归：https://cloud.tencent.com/developer/article/1339818
• 机器学习系列(1)_逻辑回归初步：https://blog.csdn.net/han_xiaoyang/article/details/49123419
• Python机器学习笔记：Logistic Regression ：https://www.cnblogs.com/wj-1314/p/10181876.html