时序模型:循环神经网络(RNN)
1. 模型定义
循环神经网络(recurrent neural network, RNN)是一类专门设计处理不定长序列数据的神经网络。
与使用一种新计算1作为核心的卷积神经网络不同,循环神经网络仍使用特征的线性组合作为计算核心,并使用共享参数策略使模型能泛化不同长度的序列数据。
2. 循环神经网络的由来:从全连接神经网络(DNN)到循环神经网络(RNN)
2.1 全连接神经网络的不足
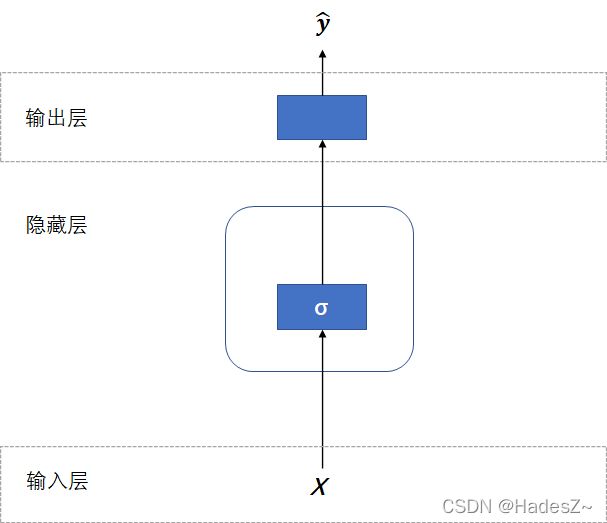
最初,研究者直接将时间序列看作特征向量,将序列每一时刻的观测作为一种特征输入全连接神经网络,来预测序列的标签。其Vanilla模型2 的结构如下图所示:
{ 输 入 层 : X = ( x 1 , x 2 , … , x n ) , X ∈ R n × d , x i ∈ R 1 × d 隐 藏 层 : Z = ϕ z ( X W x z + b z ) , W x z ∈ R d × h , b z ∈ R 输 出 层 : Y ^ = ϕ y ( X W z y + b y ) , W z y ∈ R h × q , b y ∈ R (2.1) \begin{cases} 输入层:\ & X = (x_1, x_2, \dots,x_n),\ \ X \in R^{n \times d}, \ x_i \in R^{1 \times d} \\ \\ 隐藏层: & Z = \phi_z(XW_{xz} + b_{z}), \ \ W_{xz} \in R^{d \times h}, \ b_{z} \in R \\ \\ 输出层: & \hat{Y} = \phi_y(XW_{zy} + b_{y}), \ \ W_{zy} \in R^{h \times q}, \ b_{y} \in R \end{cases} \tag {2.1} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧输入层: 隐藏层:输出层:X=(x1,x2,…,xn), X∈Rn×d, xi∈R1×dZ=ϕz(XWxz+bz), Wxz∈Rd×h, bz∈RY^=ϕy(XWzy+by), Wzy∈Rh×q, by∈R(2.1)
可见,全连接网络模型可泛化的样本要求其特征向量的维度固定(即序列长度固定),不能很好处理具有序列长度不固定特性的时间序列数据,由此发展出了循环神经网络(RNN)模型。
2.2 循环神经网络的诞生
循环神经网络先为序列每一时刻的观测,单独构建一个基于全连接网络(全连接前馈神经网络,Fully Connected Feedforward Neural Network)的子模型,来预测此时刻序列的隐藏状态(或称:隐藏变量),然后根据该隐藏状态预测出序列此时刻的标签(这是模型的输出层)。Vanilla循环神经网络(RNN)的结构如下图所示:
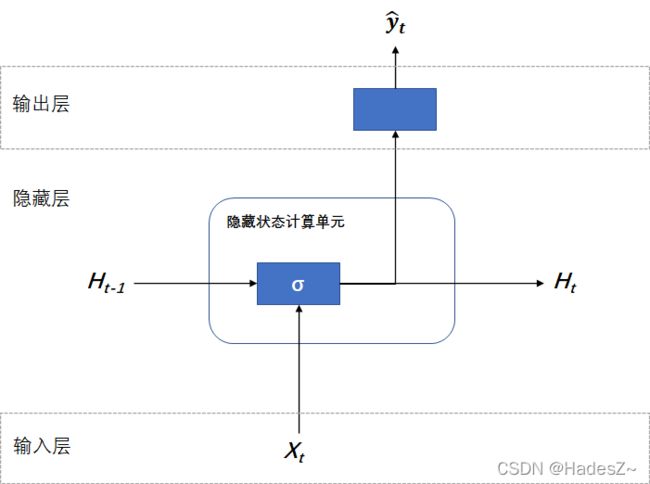
{ 输 入 层 : x t ∈ R 1 × d 隐 藏 层 : h t = ϕ h ( x t W x h + h t − 1 W h h + b h ) , W x h ∈ R d × h , W h h ∈ R h × h , b h ∈ R 输 出 层 : y ^ t = ϕ y ( h t W h y + b y ) , W h y ∈ R h × q , b y ∈ R (2.2) \begin{cases} 输入层:\ & x_t \in R^{1 \times d} \\ \\ 隐藏层: & h_t = \phi_h(x_tW_{xh} + h_{t-1}W_{hh} + b_{h}), \ \ W_{xh} \in R^{d \times h}, \ W_{hh} \in R^{h \times h}, \ b_{h} \in R \\ \\ 输出层: & \hat{y}_t = \phi_y(h_tW_{hy} + b_{y}), \ W_{hy} \in R^{h \times q}, \ b_{y} \in R \end{cases} \tag {2.2} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧输入层: 隐藏层:输出层:xt∈R1×dht=ϕh(xtWxh+ht−1Whh+bh), Wxh∈Rd×h, Whh∈Rh×h, bh∈Ry^t=ϕy(htWhy+by), Why∈Rh×q, by∈R(2.2)
由上图可见,子模型的输入为本时刻序列观测和上一时刻的隐藏状态,且在不同时间步上共享同一组线性组合的权重参数(简称:共享参数),使模型能泛化不同长度的序列数据。
如果在每个时间步上使用独立的参数,不但不能泛化到训练时没有见过的序列长度,而且也不能在时间维度上共享不同序列长度和不同位置的统计强度。当信息的特定部分会在序列内多个位置出现时,这样的共享尤为重要。
3. 循环神经网络的传播
3.1 循环神经网络的前向传播
循环神经网络的前向传播过程,先沿时间轴方向,以 图 2 图2 图2中隐藏状态计算单元为单位,从 t 1 t_1 t1 时刻传播到 t n t_n tn 时刻,形成一层单向循环神经网络;然后再沿网络层级方向,以一层循环神经网络为单位,逐层叠加形成深度循环神经网络。此外,也可以在一层网络结构中添加两组(时序)传播方向相反的单向循环神经网络,组成一层双向循环神经网络。
t t t 时刻,单向循环神经网络的前向传播公式如下所示(且深度循环神经网络和双向循环神经网络的前向传播公式与之类似,可类比得到):
{ 输 入 层 : x t ∈ R m × d 隐 藏 层 : h t = ϕ h ( x t W x h + h t − 1 W h h + b h ) , W x h ∈ R d × h , W h h ∈ R h × h , b h ∈ R 输 出 层 : y ^ t = ϕ y ( h t W h y + b y ) , W h y ∈ R h × q , b y ∈ R 损 失 函 数 : L = 1 T ∑ t = 1 T l ( y ^ t , y t ) (3.1) \begin{cases} 输入层:\ & x_t \in R^{m \times d} \\ \\ 隐藏层: & h_t = \phi_h(x_tW_{xh} + h_{t-1}W_{hh} + b_{h}), \ \ W_{xh} \in R^{d \times h}, \ W_{hh} \in R^{h \times h}, \ b_{h} \in R \\ \\ 输出层: & \hat{y}_t = \phi_y(h_tW_{hy} + b_{y}), \ W_{hy} \in R^{h \times q}, \ b_{y} \in R \\ \\ 损失函数: & L = \frac{1}{T} \sum_{t=1}^{T} l(\hat{y}_t, y_t) \end{cases} \tag {3.1} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧输入层: 隐藏层:输出层:损失函数:xt∈Rm×dht=ϕh(xtWxh+ht−1Whh+bh), Wxh∈Rd×h, Whh∈Rh×h, bh∈Ry^t=ϕy(htWhy+by), Why∈Rh×q, by∈RL=T1∑t=1Tl(y^t,yt)(3.1)
式中 m m m 代表批量大小(batch size),即每个小批量中的样本数量; d d d 代表词向量的维度; h h h, q q q 是对应隐藏层中神经元的个数。
3.2 循环神经网络的反向传播
神经网络模型采用梯度下降法得到模型参数的极大似然估计,反向传播是求损失函数对模型参数的偏导数(即参数梯度)并用其更新该模型参数的过程。
一般来讲,模型的损失函数会是一个极其复杂的复合函数,直接按导数公式求其对某模型参数偏导数的解析式十分繁琐。实践中,常根据导数的链式法则,借助计算图快速得到损失函数关于模型某参数的偏导数。在求解偏导数时,计算图将损失函数中涉及参数 θ \theta θ 的每一个子项转化成一条由损失函数节点通向模型参数节点的路径,然后将偏导数求解过程简化为求解每条路径中上一节点对本节点的导数之和的过程。且求上一节点对本节点导数时,在连接两节点的前向传播公式中,除本节点所代表参数外,所有变量均可视作常数。
为更好地说明RNN模型的反向传播过程,本文根据 式 ( 3.1 ) 式(3.1) 式(3.1)所示前向传播过程,绘制出一幅具有三个时间步的循环神经网络模型依赖关系的计算图3。图中未着色的方框表示变量,着色的方框表示参数,圆表示运算符。且为简单起见,本文将考虑一个无偏差的单向循环神经网络,并认为激活函数为恒等映射(即: ϕ ( x ) = x \phi(x) = x ϕ(x)=x)。该计算图如下所示:
{ 输 入 层 : x t ∈ R m × d 隐 藏 层 : h t = x t W x h + h t − 1 W h h , W x h ∈ R d × h , W h h ∈ R h × h , h t − 1 ∈ R m × h 输 出 层 : y ^ t = h t W h y , W h y ∈ R h × q , y ^ t ∈ R m × q 损 失 函 数 : L = 1 T ∑ t = 1 T l ( y ^ t , y t ) , L ∈ R (3.1) \begin{cases} 输入层: & x_t \in R^{m \times d} \\ \\ 隐藏层: & h_t = x_tW_{xh} + h_{t-1}W_{hh}, & \ \ \ \ W_{xh} \in R^{d \times h}, \ W_{hh} \in R^{h \times h}, \ h_{t-1} \in R^{m \times h} \\ \\输出层: & \hat{y}_t = h_tW_{hy}, & W_{hy} \in R^{h \times q}, \ \hat{y}_t \in R^{m \times q} \\ \\ 损失函数: & L = \frac{1}{T} \sum_{t=1}^{T} l(\hat{y}_t, y_t), & L \in R \end{cases} \tag {3.1} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧输入层:隐藏层:输出层:损失函数:xt∈Rm×dht=xtWxh+ht−1Whh,y^t=htWhy,L=T1∑t=1Tl(y^t,yt), Wxh∈Rd×h, Whh∈Rh×h, ht−1∈Rm×hWhy∈Rh×q, y^t∈Rm×qL∈R(3.1)
我们先沿计算图,求解反向传播中损失函数对模型各参数的偏导数(梯度)公式:
∂ L ∂ y ^ t = ∂ l ( y ^ t , y t ) T ⋅ ∂ y ^ t (3.2) \frac{\partial L}{\partial \hat{y}_t} = \frac{\partial l(\hat{y}_t, y_t)}{T \cdot\partial \hat{y}_t} \tag {3.2} ∂y^t∂L=T⋅∂y^t∂l(y^t,yt)(3.2) ∂ L ∂ W h y = ∑ t = 1 T ∂ L ∂ y ^ t h t (3.3) \frac{\partial L}{\partial W_{hy}} = \sum_{t=1}^{T} \frac{\partial L}{\partial \hat{y}_t}h_t \tag {3.3} ∂Why∂L=t=1∑T∂y^t∂Lht(3.3)
由计算图可见,损失函数对于隐藏状态 h t h_t ht 的偏导数有两种可能的情况:当 t = T t=T t=T 时, h T h_T hT 只与当前时刻模型的输出 o T o_T oT 有关;而当 t < T t
∂ L ∂ h t = { ∂ L ∂ y ^ T ∂ y ^ T ∂ h T = ∂ L ∂ y ^ T W h y , t = T ∂ L ∂ h t + 1 ∂ h t + 1 ∂ h t + ∂ L ∂ y ^ t ∂ y ^ t ∂ h t = ∂ L ∂ h t + 1 W h h + ∂ L ∂ y ^ t W h y , t < T (3.4) \frac{\partial L}{\partial h_t} = \begin{cases} \frac{\partial L}{\partial \hat{y}_T}\frac{\partial \hat{y}_T}{\partial h_T} = \frac{\partial L}{\partial \hat{y}_T}W_{hy} , & t=T \\ \\ \frac{\partial L}{\partial h_{t+1}}\frac{\partial h_{t+1}}{\partial h_{t}} + \frac{\partial L}{\partial \hat{y}_t}\frac{\partial \hat{y}_t}{\partial h_t} = \frac{\partial L}{\partial h_{t+1}}W_{hh} + \frac{\partial L}{\partial \hat{y}_t}W_{hy} , & t
将上述递归公式展开后,根据数学归纳法整理可得对任意时间步( 1 ≤ t ≤ T 1 \le t \le T 1≤t≤T)的损失函数关于隐藏状态的偏导数的通项公式:
∂ L ∂ h t = ∑ i = t T ∂ L ∂ y ^ i W h y ( ∂ h t + 1 ∂ h t ) ( T − i ) (3.5) \frac{\partial L}{\partial h_t} = \sum_{i=t}^{T} \frac{\partial L}{\partial \hat{y}_i}W_{hy}(\frac{\partial h_{t+1}}{\partial h_t})^{(T-i)} \tag {3.5} ∂ht∂L=i=t∑T∂y^i∂LWhy(∂ht∂ht+1)(T−i)(3.5)
当 h t = x t W x h + h t − 1 W h h h_t = x_tW_{xh} + h_{t-1}W_{hh} ht=xtWxh+ht−1Whh 时,得到 ∂ h t + 1 ∂ h t = W h h \frac{\partial h_{t+1}}{\partial h_t} = W_{hh} ∂ht∂ht+1=Whh(这是导致RNN模型出现梯度消失,存在长期依赖问题的根本原因),使得损失函数关于隐藏状态梯度的通项公式等于:
∂ L ∂ h t = ∑ i = t T ∂ L ∂ y ^ i W h y W h h ( T − i ) (3.6) \frac{\partial L}{\partial h_t} = \sum_{i=t}^{T} \frac{\partial L}{\partial \hat{y}_i}W_{hy}W_{hh}^{(T-i)} \tag {3.6} ∂ht∂L=i=t∑T∂y^i∂LWhyWhh(T−i)(3.6)进而得到损失函数对模型参数 W h h W_{hh} Whh 和 W x h W_{xh} Wxh 的偏导数(梯度)公式:
∂ L ∂ W h h = ∂ L ∂ h t ∂ h t ∂ W h h = ∑ i = t T ∂ L ∂ y ^ i W h y W h h ( T − i ) h t − 1 (3.7) \frac{\partial L}{\partial W_{hh}} = \frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial W_{hh}} = \sum_{i=t}^{T} \frac{\partial L}{\partial \hat{y}_i}W_{hy}W_{hh}^{(T-i)} h_{t-1} \tag {3.7} ∂Whh∂L=∂ht∂L∂Whh∂ht=i=t∑T∂y^i∂LWhyWhh(T−i)ht−1(3.7) ∂ L ∂ W x h = ∂ L ∂ h t ∂ h t ∂ W x h = ∑ i = t T ∂ L ∂ y ^ i W h y W h h ( T − i ) x t (3.8) \frac{\partial L}{\partial W_{xh}} = \frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial W_{xh}} = \sum_{i=t}^{T} \frac{\partial L}{\partial \hat{y}_i}W_{hy}W_{hh}^{(T-i)} x_{t} \tag {3.8} ∂Wxh∂L=∂ht∂L∂Wxh∂ht=i=t∑T∂y^i∂LWhyWhh(T−i)xt(3.8)
综上所述,可得到循环神经网络模型的反向传播公式:
{ W y h ′ = W y h − η m ∑ X j ∈ B a t c h ∂ L ∂ W y h = W y h − η m ∑ j = 1 m ∑ i = t T ∂ L ∂ y ^ t h t W h h ′ = W h h − η m ∑ X j ∈ B a t c h ∂ L ∂ W h h = W h h − η m ∑ j = 1 m ∑ i = t T ∂ L ∂ y ^ i W h y W h h ( T − i ) h t − 1 W x h ′ = W x h − η m ∑ X j ∈ B a t c h ∂ L ∂ W x h = W x h − η m ∑ j = 1 m ∑ i = t T ∂ L ∂ y ^ i W h y W h h ( T − i ) x j t (3.9) \begin{cases} W_{yh}^{'} = W_{yh} - \frac{\eta }{m} \sum_{X_j \in Batch}\frac{\partial L}{\partial W_{yh}} = W_{yh} - \frac{\eta }{m} \sum_{j=1}^{m}\sum_{i=t}^{T} \frac{\partial L}{\partial \hat{y}_t}h_t \\ \\ W_{hh}^{'} = W_{hh} - \frac{\eta }{m} \sum_{X_j \in Batch}\frac{\partial L}{\partial W_{hh}} = W_{hh} - \frac{\eta }{m} \sum_{j=1}^{m}\sum_{i=t}^{T} \frac{\partial L}{\partial \hat{y}_i}W_{hy}W_{hh}^{(T-i)} h_{t-1} \\ \\ W_{xh}^{'} = W_{xh} - \frac{\eta }{m} \sum_{X_j \in Batch}\frac{\partial L}{\partial W_{xh}} = W_{xh} - \frac{\eta }{m} \sum_{j=1}^{m}\sum_{i=t}^{T} \frac{\partial L}{\partial \hat{y}_i}W_{hy}W_{hh}^{(T-i)} x_{jt} \end{cases} \tag {3.9} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Wyh′=Wyh−mη∑Xj∈Batch∂Wyh∂L=Wyh−mη∑j=1m∑i=tT∂y^t∂LhtWhh′=Whh−mη∑Xj∈Batch∂Whh∂L=Whh−mη∑j=1m∑i=tT∂y^i∂LWhyWhh(T−i)ht−1Wxh′=Wxh−mη∑Xj∈Batch∂Wxh∂L=Wxh−mη∑j=1m∑i=tT∂y^i∂LWhyWhh(T−i)xjt(3.9)
由上述反向传播公式4可见,当 T − i T-i T−i 较大时, W h h W_{hh} Whh 中小于1的特征值将会消失(趋近于0),大于1的特征值将会发散(趋近于无穷大)。这导致训练过程中,模型参数 W h h W_{hh} Whh 和 W x h W_{xh} Wxh 容易出现梯度消失和梯度爆炸现象,使距离句子结尾较远处单词的信息不再影响模型参数地更新(即:模型不能学习到距离句子结尾处较远的单词所蕴含的特征信息),这被称作RNN模型的长期依赖问题。
4. 模型的代码实现
循环神经网络的实现代码如下,分别给出了基于目前两大主流框架的实现。值得注意的是循环神经网络中,隐藏层的参数初始化方法,其中上一时刻隐藏状态的权重参数 W h h W_{hh} Whh 应采用正交初始化(Orthogonal Initialization)方法,以避免在沿时间步传播过程中出现梯度消失或梯度爆炸现象。而本时刻输入的权重参数 W x h W_{xh} Wxh 不涉及深度网络传播,可采用正常的 Xavier uniform 初始化方法。在LSTM、GRU等其他RNN类网络中,参数的初始化方法与此一致。
4.1 TensorFlow 框架实现
4.2 Pytorch 框架实现
"""
v2.0 修复RNN参数初始化不当,引起的时间步传播梯度消失问题。 2022.04.28
"""
import torch
from torch import nn
from torch.nn import functional as F
from torch.nn.parameter import Parameter
#
class Simple_RNN_Cell(nn.Module):
def __init__(self, token_dim, hidden_dim
, activation=nn.Tanh()
, use_bias=True
, kernel_initializer=nn.init.xavier_uniform_
, recurrent_initializer=nn.init.orthogonal_
, bias_initializer=nn.init.zeros_
, device="cpu"):
super().__init__()
# 超参定义
self.hidden_dim = hidden_dim
self.device = device
self.kernel_initializer = kernel_initializer
self.recurrent_initializer = recurrent_initializer
self.bias_initializer = bias_initializer
#
self.Hidden = nn.Linear(token_dim, hidden_dim, bias=use_bias).to(self.device)
self.RecurHidden = nn.Linear(hidden_dim, hidden_dim, bias=use_bias).to(self.device)
self.Activation = activation.to(self.device)
# 参数初始化
self.kernel_initializer(self.Hidden.weight)
self.recurrent_initializer(self.RecurHidden.weight)
self.bias_initializer(self.Hidden.bias), self.bias_initializer(self.RecurHidden.bias)
def forward(self, inputs, last_state: list):
hidden = self.Hidden(inputs)
recur_hidden = self.RecurHidden(last_state[-1])
hidden = self.Activation(
hidden + recur_hidden
)
return [hidden]
def zero_initialization(self, batch_size):
return [torch.zeros([batch_size, self.hidden_dim]).to(self.device)]
#
class RNN_Layer(nn.Module):
"""
bidirectional: If ``True``, becomes a bidirectional RNN network. Default: ``False``.
padding: String, 'pre' or 'post' (optional, defaults to 'pre'): pad either before or after each sequence.
"""
def __init__(self, rnn_cell, bidirectional=False, pad_position='post'):
super().__init__()
self.RNNCell = rnn_cell
self.bidirectional = bidirectional
self.padding = pad_position
def forward(self, inputs, mask=None, initial_state=None):
"""
inputs: it's shape is [batch_size, time_steps, token_dim]
mask: it's shape is [batch_size, time_steps]
:return
sequence: it is hidden state sequence, and its' shape is [batch_size, time_steps, hidden_dim]
last_state: it is the hidden state of input sequences at last time step,
but, attentively, the last token wouble be a padding token,
so this last state is not the real last state of input sequences;
if you want to get the real last state of input sequences, please use utils.get_rnn_last_state(hidden state sequence).
"""
batch_size, time_steps, token_dim = inputs.shape
#
if initial_state is None:
initial_state = self.RNNCell.zero_initialization(batch_size)
if mask is None:
if batch_size == 1:
mask = torch.ones([1, time_steps]).to(inputs.device.type)
elif self.padding == 'pre':
raise ValueError('请给定掩码矩阵(mask)')
elif self.padding == 'post' and self.bidirectional is True:
raise ValueError('请给定掩码矩阵(mask)')
# 正向时间步循环
hidden_list = []
hidden_state = initial_state
last_state = None
for i in range(time_steps):
hidden_state = self.RNNCell(inputs[:, i], hidden_state)
hidden_list.append(hidden_state[-1])
if i == time_steps - 1:
"""获取最后一时间步的输出隐藏状态"""
last_state = hidden_state
if self.padding == 'pre':
"""如果padding值填充在序列尾端,则正向时间步传播应加 mask 操作"""
hidden_state = [
hidden_state[j] * mask[:, i:i + 1] + initial_state[j] * (1 - mask[:, i:i + 1]) # 重新初始化(加数项作用)
for j in range(len(hidden_state))
]
sequence = torch.reshape(
torch.unsqueeze(
torch.concat(hidden_list, dim=1)
, dim=1)
, [batch_size, time_steps, -1]
)
# 反向时间步循环
if self.bidirectional is True:
hidden_list = []
hidden_state = initial_state
for i in range(time_steps, 0, -1):
hidden_state = self.RNNCell(inputs[:, i - 1], hidden_state)
hidden_list.insert(0, hidden_state[-1])
if i == time_steps:
"""获取最后一时间步的cell_state"""
last_state = [
torch.concat([last_state[j], hidden_state[j]], dim=1)
for j in range(len(hidden_state))
]
if self.padding == 'post':
"""如果padding值填充在序列首端,则正反时间步传播应加 mask 操作"""
hidden_state = [
hidden_state[j] * mask[:, i - 1:i] + initial_state[j] * (1 - mask[:, i - 1:i]) # 重新初始化(加数项作用)
for j in range(len(hidden_state))
]
sequence = torch.concat([
sequence,
torch.reshape(
torch.unsqueeze(
torch.concat(hidden_list, dim=1)
, dim=1)
, [batch_size, time_steps, -1]
)
], dim=-1)
return sequence, last_state
卷积神经网络(convolutional neural netword, CNN)以卷积运算(convolution)或更直观的互相关运算(cross-crorelation)作为计算核心。 ↩︎
Vanilla模型指:最初的、最简单版本的模型,即该种模型的原型。 ↩︎
图片摘自《动手学深度学习》的RNN讲解章节 ↩︎
式 ( 3.8 ) 式(3.8) 式(3.8) ↩︎