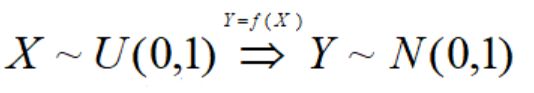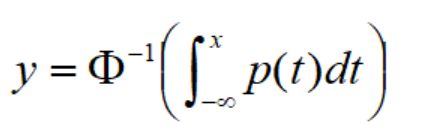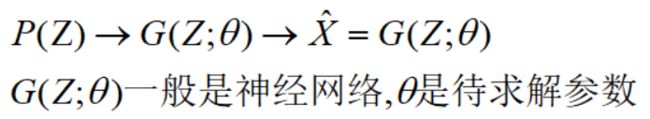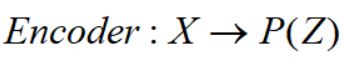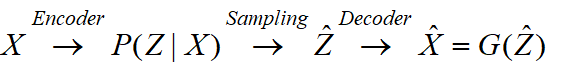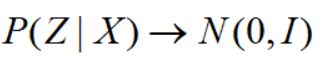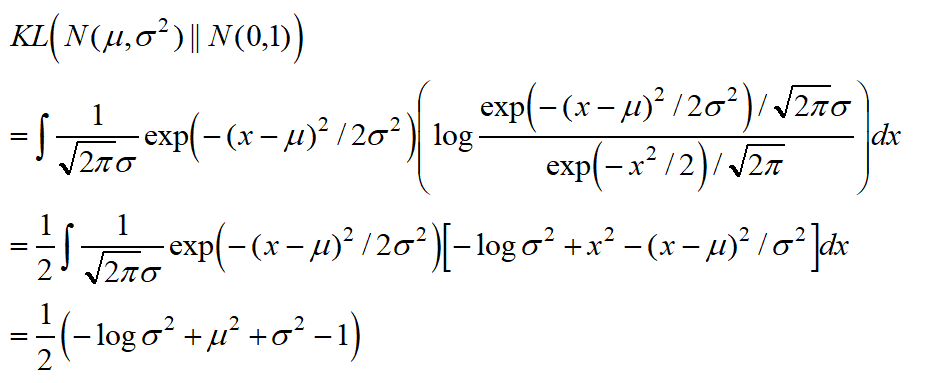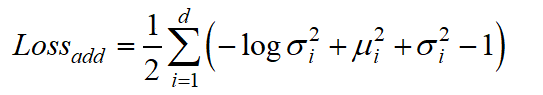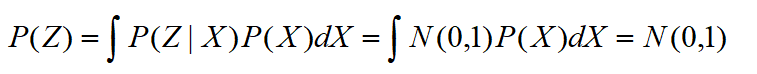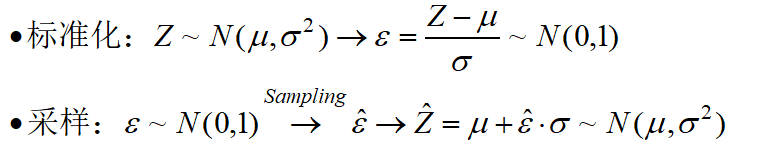带你看懂变分自编码(VAE)

编码器（AutoEncoder, AE）是一类神经网络，其功能是通过将输入信息作为学习目标，对输入信息进行表征学习。在结构上是一种对称的网络，本文对它不做单独介绍，而是以变分自编码（Variational AutoEncoder）来理解它。

实际上，我们在机器学习篇章中对VAE从理论上做了一次介绍，还是比较晦涩难懂的。今天，我们就由浅入深来详细理解一下这个由世界级顶尖研究型大学——阿姆斯特丹大学——学霸提出来的研究成果。

传送门：变分自编码（VAE）

用已知分布逼近任意分布

首先，考虑下面情景：

假设已知一个能生成服从均匀分布U(0,1)的生成器，请问如何利用它生成服从正态分布的伪随机样本？

根据中心极限定理，只要对每次生成m个样本的均匀分布求和，作为一个新样本，重复n次，那么n个样本服从正态分布。但这里我们想得到更一般的方法：

即X经过f映射后，得到的Y服从正态分布。如果f存在，很显然有：

于是得到：

Φ是正态分布累计分布函数，它的显式表达式不好求，而且还是逆函数，更加难以求解。那怎么办呢。那就用神经网络吧，它可以逼近任意函数。

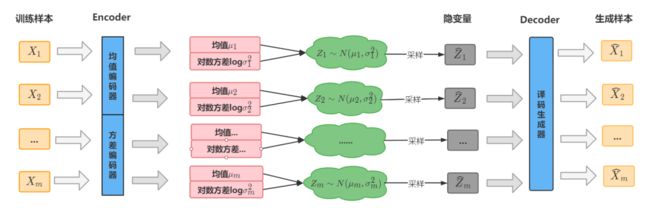
VAE实现框架

实际上，VAE模型是构建一个从隐变量 Z 生成目标数据 X 的模型，更准确的说，利用某些常见的分布（这里是正态分布），然后训练一个模型 X=G(Z)，这个模型能够将原来的简单概率分布映射到训练集的真实概率分布，也就是说，VAE的本质是利用一个简单概率分布去逼近训练集的真实分布：

这部分是译码部分（decoder），我们还要利用训练集X的信息去encoder简单概率分布P(Z)：

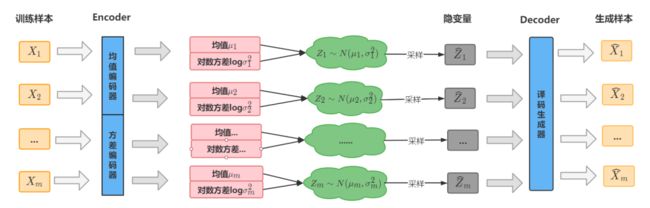
这里要考虑两点：Z是假设服从正态分布，encoder要对应均值和方差两个参数；采集到的样本Z要准确对应编码前的是来自哪一个样本X。

因此VAE的编码过程是假设隐变量Z关于每一个样本后验都服从一个正态分布P(Z|X)，这样P(Z)采集到的Z就与某个样本唯一对应；训练时每一个样本都训练两个目标——均值和对数方差(方差恒大于0,神经网络训练需要再做转换，因此直接计算其对数，则取值范围是实数)：

这就是VAE的实现框架，它为每个样本构造特定的正态分布(后验)，然后基于这个后验采样来重新生成样本，前者是编码过程，后者是译码过程。

变分体现在哪里

通过上图可以知道，译码过程是通过采样实现的，不是直接利用编码的结果，这一点与普通的Autoencoder不同，所以这个过程会受到噪声(也就是方差)的影响，因此为了使得重构效果好，模型应该会想办法使得方差趋于0。但如果方差为0，这样就没有随机性了，所有采样的样本都集中在一点上。

如果这样，模型就变成了普通的Autoencoder。为了防止其噪声为零，同时保证该模型具有生成能力，VAE让所有的后验分布p(Z|X) 向标准正态分布看齐：

利用KL散度实现这个想法，这里假设隐变量Z每个维度是独立的：

因此，在Autoencoder基础上，加上重构误差：

d就是隐变量Z的维度.

我们还可以看到，如果所有后验逼近标准正态分布，那么：

正好与假设相吻合，也就是让后验分布逼近先验假设分布，保证生成能力。

KL散度也称为变分，在变分推断已经做过介绍。因此，VAE被称为变分自编码的原因是因为损失增加了KL散度，使得所有后验P(Z|X)向标准正态分布看齐。

传送门：变分推断（Variational Inference）

重参数技巧与正则化

实现采样的时候，利用了重参数技巧，它的思路实际是正态分布标准化：

因此采样过程，实际上是从标准正态分布采样即可。

我们可以看到，整个VAE实现过程中，重点是编码过程，它与普通encoder不同的地方在于：

第一，有两个encoder，一个是计算均值，一个是计算方差；

第二，KL散度损失实际是一个正则项，使得编码结果具有零均值且有一定噪声；

第三，encoder的结果不直接作为decoder的输入，而是通过采样后再进行译码

基于keras实现VAE

理解了原理，我们来看看利用tensorflow来实现一个标准的VAE。实例参考自tensorflow官网，先介绍用到的数据集mnist:

数据集是手写数字，训练集为 60,000 张 28x28 像素灰度图像，测试集为 10,000 同规格图像，总共 10 类数字标签。

from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()

x是图片矩阵，尺寸为 (num_samples, 28, 28)；y是对应的标签0~9整数。用plt可以可视化：

下面是编写VAE代码，先导入必要的包：

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

然后编写四个函数：

• 采样函数Sampling，从标准正态分布采样，经过重参数化技巧输出最终采样样本，核心代码是：

#从标准正态分布采样batch个样本，维度是dim
epsilon = tf.keras.backend.random_normal(shape=(batch, dim)) 


#映射为编码后的正态分布样本
z_mean + tf.exp(z_log_var) * epsilon

• 编码函数Encoder,训练样本x编码两次，计算均值和方差，核心代码是：

#均值编码器，生成与训练集样本个数相同的均值个数
z_mean = self.dense_mean(x) 


#对数方差编码器，生成与训练集样本个数相同的对数方差个数
z_log_var = self.dense_log_var(x)

• 译码函数Decoder,将采样的隐变量Z通过生成器生成样本，代码就是神经网路层，与编码层对应

self.dense_proj = layers.Dense(intermediate_dim, activation="relu")
self.dense_output = layers.Dense(original_dim, activation="sigmoid")

• 最后还要写一个函数把编码、采样、译码连接起来，并且在此过程添加KL损失函数，核心代码是：

#编码，获得每个样本对应的均值、方差以及采样的隐变量
z_mean, z_log_var, z = self.encoder(inputs)


#译码，对采样的隐变量生成样本
reconstructed = self.decoder(z)


# 在此过程添加额外的损失函数——KL散度，对Autoencoder惩罚
kl_loss = -0.5 * tf.reduce_mean(
            z_log_var - tf.square(z_mean) - tf.exp(z_log_var) + 1)
self.add_loss(kl_loss)

源码如下：

class Sampling(layers.Layer):
    """Uses (z_mean, z_log_var) to sample z, the vector encoding a digit."""

    def call(self, inputs):
        z_mean, z_log_var = inputs
        batch = tf.shape(z_mean)[0]
        dim = tf.shape(z_mean)[1]
        epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
        return z_mean + tf.exp(0.5 * z_log_var) * epsilon


class Encoder(layers.Layer):
    """Maps MNIST digits to a triplet (z_mean, z_log_var, z)."""

    def __init__(self, latent_dim=32, intermediate_dim=64, name="encoder", **kwargs):
        super(Encoder, self).__init__(name=name, **kwargs)
        self.dense_proj = layers.Dense(intermediate_dim, activation="relu")
        self.dense_mean = layers.Dense(latent_dim)
        self.dense_log_var = layers.Dense(latent_dim)
        self.sampling = Sampling()

    def call(self, inputs):
        x = self.dense_proj(inputs)
        z_mean = self.dense_mean(x)
        z_log_var = self.dense_log_var(x)
        z = self.sampling((z_mean, z_log_var))
        return z_mean, z_log_var, z


class Decoder(layers.Layer):
    """Converts z, the encoded digit vector, back into a readable digit."""

    def __init__(self, original_dim, intermediate_dim=64, name="decoder", **kwargs):
        super(Decoder, self).__init__(name=name, **kwargs)
        self.dense_proj = layers.Dense(intermediate_dim, activation="relu")
        self.dense_output = layers.Dense(original_dim, activation="sigmoid")

    def call(self, inputs):
        x = self.dense_proj(inputs)
        return self.dense_output(x)


class VariationalAutoEncoder(keras.Model):
    """Combines the encoder and decoder into an end-to-end model for training."""

    def __init__(
        self,
        original_dim,
        intermediate_dim=64,
        latent_dim=32,
        name="autoencoder",
        **kwargs
    ):
        super(VariationalAutoEncoder, self).__init__(name=name, **kwargs)
        self.original_dim = original_dim
        self.encoder = Encoder(latent_dim=latent_dim, intermediate_dim=intermediate_dim)
        self.decoder = Decoder(original_dim, intermediate_dim=intermediate_dim)

    def call(self, inputs):
        z_mean, z_log_var, z = self.encoder(inputs)
        reconstructed = self.decoder(z)
        # Add KL divergence regularization loss.
        kl_loss = -0.5 * tf.reduce_mean(
            z_log_var - tf.square(z_mean) - tf.exp(z_log_var) + 1
        )
        self.add_loss(kl_loss)
        return reconstructed

最后进行训练，输入是训练集，输出也是训练集

ae = VariationalAutoEncoder(784, 64, 32)


optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
vae.compile(optimizer, loss=tf.keras.losses.MeanSquaredError())


x_train = x_train.reshape(60000, 784).astype("float32") / 255
vae.fit(x_train, x_train, epochs=20, batch_size=64,validation_split=0.2)

这样就完成了一个标准的VAE。完美，收工，周末愉快！！！

参考资料：

http://cn.arxiv.org/pdf/1312.6114v10

https://tensorflow.google.cn/guide/keras/custom_layers_and_models