笔记：Self-Taught Low-Rank Coding for Visual Learning

Li, S., K. Li and Y. Fu, Self-Taught Low-Rank Coding for Visual Learning. IEEE Transactions on Neural Networks and Learning Systems, 2017. PP(99): p. 1-12.
本文是这篇 Trans. on NNLS 期刊论文的笔记，主要是对文中的理论方法进行展开详解。本人学术水平有限，文中如有错误之处，敬请指正。

摘要： 计算机视觉和机器学习研究中，缺少标签数据是一个常有的挑战。半监督学习和迁移学习，已经被用于应对这种问题，通过使用来自相同领域、或不同领域的，辅助的样本。自我学习是一种特殊的迁移学习，在选择辅助数据上有更少的限制。这已经在视觉学习上有良好的表现。然而，现有的自我学习方法通常忽视了数据的结构信息。此文关注点在建立一个自我学习编码框架，有效地使用丰富的低级的模式信息（提取于辅助领域），为了在目标领域中表示高级的结构信息。通过利用从辅助领域和目标领域学习到的高质量的字典，此方法可以在目标领域学习到样本的表示编码。已经有许多类型的视觉数据被证明有子空间结构，低秩约束加入到目标中，更好地表示目标集。此文提出的表示学习框架称为自学习低秩编码（self-taught low-rank (S-Low) coding），可以建模为一个非凸的秩最小化和字典学习的问题。此文也使用，最小化的増广 Lagrange 乘子法。根据提出的编码框架，同时推导出了非监督和有监督的算法。

1 简介

好的特征是能表达出来的，是一个合理大小的字典，可以捕获到大量输入数据，表征一个给予的数据集的全局结构。然而，缺少训练数据使得特征学习变得非常复杂。

半监督学习利用一些带标签的样本和大量无标签的样本，它们来自相同的领域，有相同的分布，去训练模型。半监督学习还是有局限性。迁移学习中，限制被放松了。其中，标签样本和辅助样本来自不同的集合，有不同的分布。但是迁移学习中，要求两个领域是相似的。许多的迁移学习算法假设两个领域都有相似的知识结构。所以，半监督学习和迁移学习在辅助（源）数据上都有强约束条件，限制了其应用。最近出现的机器学习模型——自我学习（STL）1 2 3 4 5，使用无标签数据，带有很少的约束，提升了图像聚类和分类的性能。

自我学习和迁移学习是两个相关的概念。关键的差异是它们在辅助领域的约束不同。具体来说，迁移学习只利用同类的任务的标签数据，而自我学习（更宽松）利用来自辅助领域的随机图像。简单来说，自我学习随机从辅助领域选择的视觉数据，仍可以包含一些基本的视觉模式（边缘、角、形状），与目标领域的特征极其相似。这灵活性使得自我学习特别有潜力适用大量的无标签的数据。现有的一些自我学习方法，忽视了目标领域中的结构信息（这个在图像分类中很重要）。

此文提出了一种新的自我学习低秩编码（S-Low coding）框架。通过利用从辅助领域中提取的高质量的字典，可以学习在目标领域中的高级表示。由于许多视觉数据可以很好地用子空间结构表示 6 7，此文介绍了一种低秩约束，利用目标领域中的全局结构信息。此文的方法可以适用于许多应用：目标检测、场景分类、人脸识别、图像聚类。特别当目标数据很少时，此方法仍可以提取有效地特征表示，借助辅助领域中的大规模的无标签数据。同时，低秩约束能够移除噪声或异常点 8 9 10 。

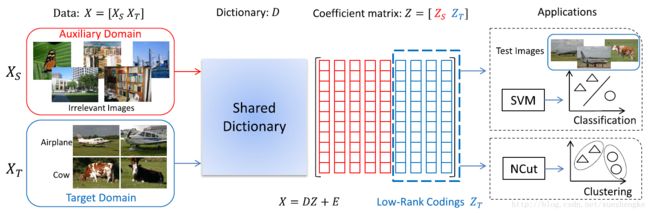
自我学习低秩编码（S-Low coding）流程。较少的目标数据集 XT 通常不够，对于提取出有效的特征。通过使用额外的辅助数据集 XS ，此文提出的框架学习到了一个共享的字典 D 从两个领域中，并加入了一个低秩约束于系数矩阵的目标领域 ZT 上，让其成为新的特征表示。最后，使用 NCut 算法进行图像聚类；SVM 算法用于图像分类。此文的方法可以抽象成一个秩最小化问题和字典学习问题。此文设计了一个高效的最小化优化算法，同时学习低秩编码和字典。目标领域的数据对应的低秩编码部分，可以直接用于训练监督模型，进行聚类或分类。

此文提出的方法可以解决一些现有方法的限制。首先，现有的方法给特定的应用设计算法。而此文提出的方法可以被用于监督和非监督的任务。其次，现有的自我学习方法仅仅从目标领域中学习新的特征，却忽视了重要的全局的结构信息。此文的方法可以利用从辅助领域提取的低级的模式信息，来表示目标领域中的高级的结构信息。

此文的主要贡献有：

• 有了辅助领域的大量的模式信息，S-Low 编码方法可以更好地学习到特征表示，在目标领域中加入低秩约束。

• 此文提出的方式是一个通用的框架，可以用于多种视觉学习场景。此文给出了非监督学习和监督学习的详细的算法。

• 不像其他 LRR 算法（使用有偏估计， ℓ1 范数和核范数），此文将 ℓ0 范数核 rank 函数替换成最小最大凹惩罚范数（minimax concave penalty norm, MCP）和矩阵 γ 范数，这是无偏估计的。我们设计了最小化优化算法，并经验性地给出了其收敛性质。

2 相关工作

略

3 自学习低秩编码

3.1 动机

略

3.2 优化算法

考虑无标签样本 XS={xS1,xS2,⋯,xSm}∈Rd×m 来自辅助领域，和 XT={xT1,xT2,⋯,xTn}∈Rd×n 于目标领域。此文的方法目标是学习表达性的编码，表示子空间结构信息，于目标领域。与其他自我学习方法一致，此文并不假设来自辅助域和目标域的数据有相同（或相似）的分布。另外，此文并不要求来自目标域的样本带有标签。所以，此方法既可以用于非监督形式，也可以用于有监督形式，这与 文献 11 和 12 的问题不一样。所以此方法可以处理聚类问题（如果标签未知）和分类问题（如果标签已知）。

传统的稀疏编码 13，字典学习 14，低秩学习 15 方法近似表达样本在一个域中

XT≈DTZT,(1)

其中 ZT∈Rr×n 是表示的系数矩阵， DT∈Rd×r 是字典， r 是字典的大小（列）。 ZT 通常期望是稀疏的或低秩的。 DT 有时就设为样本数据自身，即 DT=XT ，有可能会出现不充分样本的问题。有了辅助领域的数据，就可以学习到更有信息量的字典，解决这个不充分样本的问题。

首先，此方法可以从两个领域中的所有样本中学习字典。数据集 X=[XS,XT] 。目标是用字典 D∈Rd×r 来表示 X 。于是介绍这个约束 [XS,XT]=D[ZS,ZT]+[ES,ET]，其中 ZS∈Rr×m,ZT∈Rr×n 是对应辅助领域和目标领域的系数矩阵。 ES∈Rd×m,ET∈Rd×n 是对应辅助领域和目标领域，分离出的稀疏的噪声矩阵。 ES,ET 一般用 ℓ0 范数的代替约束，比如 ℓ1 或 ℓ2,1 范数。在实际中，目标样本中通常包含许多的噪声。考虑了加噪声的模型，使得学习到的字典更具有鲁棒性。

其次，在许多的聚类和分类的问题中，目标领域中的样本通常有隐含的子空间结构。研究表明，使用低秩约束，可以有效地发现潜在的子空间结构。利用这子空间结构信息对学习过程很有利。根据观察，将约束加于 ZT ，目标函数给出如下

minD,ZS,ZT,ES,ET s.t.rank(ZT)+λ1||ES||0+λ2||ET||0XS=DZS+ES, XT=DZT+ET,(2)

其中 rank(⋅) 表示秩函数， ||⋅||0 表示 ℓ0 范数， λ1,λ2 是权衡系数。公式中第一项，表示 ZT 的低秩性质，后两项模拟重建误差。这是秩最小化问题的变形，一般来说是 NP-hard，所以不能直接求解。在实际求解中，通常使用 ℓ1 范数和核范数来代替 ℓ0 范数和 rank 函数。这样就可以使用交替方向乘子法来求解。然而， 16 表明， ℓ1 范数和核范数是有偏估计，它们过度惩罚了大的矩阵元素和大的奇异值。所以此文使用非凸的 最小最大凹惩罚范数（minimax concave penalty, MCP）范数和矩阵 γ 范数 代替，进行求解。
矩阵 B∈Rp×q 的 MCP 范数定义 17 如下

Mλ,γ(B)=∑i,jϕλ,γ(Bi,j),ϕλ,γ(t)=λ∫t0[1−xλγ]+dx=⎧⎩⎨γλ22,γ|t|−t22γ,if |t|≥γλ,otherwise.(3)

[z]+=max(z,0) 。此文中， λ=1 ，简便记法 Mγ(B)=M1,γ(B) 。矩阵的 γ 范数定义 18 为

||B||γ=∑i=1s∫σi(B)0(1−uγ)+du=∑i=1sϕ1,γ(σi(B))=Mγ(σ(B)), γ>1,(4)

其中 σ(B)=(σ1(B),σ2(B),⋯,σs(B))T 表示形式 Rp×q→Rs×1+, s=min(p,q) 。很明显，矩阵的 γ 范数是关于 B 非凸的。替换之后目标函数重写为

minD,ZS,ZT,ES,ET s.t.||ZT||γ1+λ1Mγ2(ES)+λ2Mγ2(ET)XS=DZS+ES, XT=DZT+ET.(5)

字典从辅助领域和目标领域一起学习到，为了学习到有用的信息。公式中的两个约束都共用一个字典 D 。由于 XS 包含的样本数通常多于 XT ，所以学习的字典很容易是被辅助域的数据决定的。然而，更重要的是字典 D 对目标领域数据的重建能力。所以，此文加入了对 ZS 的 ℓ2,1 约束。这样的方式，使得 ZS 中的某一些行接近于 0，使其适应从字典 D 中选择基。目标函数变成

minD,ZS,ZT,ES,ET s.t.||ZT||γ1+λ1Mγ2(ES)+λ2Mγ2(ET)+λ3||ZS||2,1XS=DZS+ES, XT=DZT+ET.(6)

其中 λ3 是权衡参数， ||ZS||2,1=∑nj=1(∑di=1[ZS]2i,j)1/2 是 ℓ2,1 范数。系数矩阵 ZT 的每一列对应目标领域中的一个样本，也就是此文提及的低秩编码（low-rank coding）。

3.3 优化

此文使用优化最小化增广拉格朗日乘子(MM-ALM)算法（majorization–minimization augmented Lagrange multiplier, MM-ALM）求解。首先介绍通用的 shrinkage 操作和 singular value shrinkage 操作，

[Dγ,W(B)]ij=sign(Bij)⋅(|Bij|−τWij)+,Sτ,Λ(X)=UXDγ,Λ(ΣX)VTX,(7)

其中 Λ,Σ 都是非负的矩阵。为了帮助优化，加入一个松弛变量 J∈Rr×n ，

minD,ZS,ZT,ES,ET,J s.t.||J||γ1+λ1Mγ2(ES)+λ2Mγ2(ET)+λ3||ZS||2,1XS=DZS+ES, XT=DZT+ET, ZT=J.(8)

MM-ALM 算法包含内循环和外循环。每一次迭代中，外循环使用局部线性近似（locally linear approximation, LLA）处理原始的非凸问题，并组成一个加权的凸优化问题；在内循环中，采用 inexact ALM 算法。

在外循环中，需要重写目标函数。因为原目标函数关于 (σ(J),|ES|,|EJ|) 是凹的，可以将 ||J||γ1+λ1Mγ2(ES)+λ2Mγ2(ET) 代替为 (σ(Jold),|ES|old,|EJ|old) 的一阶近似。新的目标函数写为

minD,ZS,ZT,ES,ET,J s.t.Qγ1(σ(J)|σ(Jold))+λ1Qγ2(ES|EoldS)+λ2Qγ2(ET|EoldT)+λ3||ZS||2,1XS=DZS+ES, XT=DZT+ET, ZT=J,(9)

其中一阶近似项表达为

Qγ(B|Bold)=Mγ(Bold)+∑i,j(1−|Boldij|/γ)+⋅(|Bij−|Boldij|).(10)

在内循环中，采用 inexact ALM 算法进行优化。已有初始化过的字典 D ，需要更新的变量是 J,ZS,ZT,ES,ET 。写出増广 Lagrangian 函数如下

L=Qγ1(σ(J)|σ(Jold))+λ1Qγ2(ES|EoldS)+λ2Qγ2(ET|EoldT)+λ3||ZS||2,1+tr(RT(ZT−J))+tr(YT(XS−DZS−ES))+tr(QT(XT−DZT−ET))+μ2(||ZT−J||2F+||XS−DZS−ES||2F+||XT−DZT−ET||2F),(11)

其中 ||⋅||F 是 Frobenius 范数， Y∈Rd×m,Q∈Rd×n,R∈Rr×n 是 Lagrange 乘子矩阵， μ 是一个正的惩罚系数。在第 k+1 次迭代中，按如下的顺序轮流更新变量

Jk+1=S1/μ,Λ(ZTk+Rk/μk),ZT(k+1)=(In+DTD)−1(DTXT−DTETk+Jk+1+(DTQk−Rk)/μk),ZS(k+1)=argminZS λ3μk||ZS||2,1+12||ZS−ZSk−DT(XS−DZSk−ESk+Yk/μk)||2F,ES(k+1)=Dλ1/μ,W(XS−DZS(k+1)+Yk/μk),ET(k+1)=Dλ2/μ,W(XT−DZT(k+1)+Qk/μk).(12)(13)(14)(15)(16)

之后再更新字典 D ，固定其它变量，

Dj+1=argminD tr(YT(XS−DZS−ES))+tr(QT(XT−DZT−ET))+μ2(||XS−DZS−ES||2F+||XT−DZT−ET||2F)=[1μ(YZTS+QZTT)+(XS−ES)ZTS+(XT−ET)ZTT](ZSZTS+ZTZTT)−1.(17)

内循环和外循环重复进行直至收敛。整体的算法于 Algorithm 1 中给出。

---

Algorithm 1 MM-ALM Algorithm
Input: 数据 X=[XS,XT] ,
常系数 λ1,λ2,λ3 , D0,J0,ZT0,ZS0,ES0,ET0,Y0,Q0,R0 ,
ρ=1.2, μ0=10−3, μmax=105, k=0, ϵ=10−6 .
1: while not converged do
2: W=(1m1Tn−|Sj|/γ2)+ ;
3: Λ=diag(1n−σ(Jj)/γ1)+ ;
4: while not converged do
5: 更新 Jj+1k+1 ;
6: 更新 Zj+1T(k+1) ;
7: 更新 Zj+1S(k+1) ;
8: 更新 Ej+1S(k+1) ;
9: 更新 Ej+1T(k+1) ;
10: 更新 Y,Q,R

Yk+1Qk+1Rk+1=Yk+μk(XS−Dj+1Zj+1S(k+1)−Ej+1S(k+1));=Qk+μk(XT−Dj+1Zj+1T(k+1)−Ej+1T(k+1));=Rk+μk(Jj+1k+1−Zj+1T(k+1));

11: 更新 μk+1=min(μmax,ρμk) ;
12: 检查收敛条件

||XS−DZS−ES||∞<ϵ, ||J−ZT||∞<ϵ, ||XT−DZT−ET||∞<ϵ ;

13: k=k+1 ;
14: end while
15: 更新 Dj+1 ;
16: j=j+1 ;
17: end while
Output: ZS,ZT,ES,ET,D .

---

3.4 分析

此文提出的算法有局部的收敛性：当字典 D 是固定时，目标函数满足如下

Qγ(B|Bold)=Mγ(Bold)+∑i,j(1−|Boldij|/γ)+⋅(|Bij−|Boldij|)≤Qγ(Bold|Bold),f(J,ES,ET,ZS)=Qγ1(σ(J)|σ(Jold))+λ1Qγ2(ES|EoldS)+λ2Qγ2(ET|EoldT)+λ3||ZS||2,1≤Qγ1(σ(Jold)|σ(Jold))+λ1Qγ2(EoldS|EoldS)+λ2Qγ2(EoldT|EoldT)+λ3||ZoldS||2,1=f(Jold,EoldS,EoldT,ZoldS).

在初始化时，字典 D 是用 X 的样本随机构成的。 ZS,ZT 是用小的随机值初始化的，其它变量都初始化为 0 。实验发现， D,Z 的初始值对结果并不敏感。

时间复杂度：假设 r<n ，Algorithm 1 的第 5 步，需要 SVD 计算 矩阵 r×n ，消耗 O(nr2) ；而第 6 步中的矩阵求逆需要 O(nr2) 。因为外部循环收敛较快，所以这里只考虑内部循环的时间复杂度。假设 t 是内部循环的迭代次数，那么粗略计算该算法的复杂度为 O(tnr2) 。

4 S-Low 编码学习

S-Low 聚类

有了无标签的数据集 X=[XS,XT] ，S-Low 聚类的目标是恢复目标域的潜在子空间结构。低秩编码 ZT 用于定义一个无向图 G 的亲和矩阵。根据低秩子空间恢复理论，系数矩阵 Z 的每一列都代表一个数据样本的新的表示。那么每一对样本的相关系数是作为其在无向图中对应边的权值的最好选择。这里用余弦相似度来定义其权值。给定 zi,zj∈ZT ，图的权值 G(i,j) 定义为

G(i,j)=zTizj||zi||2||zj||2.

另一方面，稀疏性在图构建过程中也是强调的，所以通过修剪一些小的权值使其变得更稀疏。最后，有效的聚类算法，比如 normalized cuts (NCuts) 用于给出聚类的结果。

S-Low 分类

当目标领域中的样本标签都已知，可以设计一个分类算法基于 S-Low 编码，训练一个分类器。有了字典 D ，就可以分类新的样本。正如之前所述，低秩编码 ZT可以作为目标样本 XT 的新表示。有了一个测试样本 y ，可以计算其系数表示 y∈Rd×1，通过

mina ||y−Da||22+λ||a||1,

其中 a∈Rr×1 是 y 基于字典 D 的系数向量。不失一般性，可以使用 ZT 训练任何的分类器。此文采用常用的分类器 SVM，预测新样本 $y$ 的类别标签。

实验

略

---

1. R. Raina, A. Battle, H. Lee, B. Packer, and A. Y. Ng, “Self-taught learning: Transfer learning from unlabeled data,” in Proc. 24th Int. Conf. Mach. Learn., 2007, pp. 759–766. ↩
2. W. Dai, Q. Yang, G.-R. Xue, and Y. Yu, “Self-taught clustering,” in Proc. 25th Int. Conf. Mach. Learn., 2008, pp. 200–207. ↩
3. R. Raina, “Self-taught learning,” Ph.D. dissertation, Dept. Comput. Sci. Stanford Univ., Stanford, CA, USA, 2009. ↩
4. H. Wang, F. Nie, and H. Huang, “Robust and discriminative self-taught learning,” in Proc. 30th Int. Conf. Mach. Learn., 2013, pp. 298–306. ↩
5. J. Kuen, K. M. Lim, and C. P. Lee, “Self-taught learning of a deep invariant representation for visual tracking via temporal slowness principle,” Pattern Recognit., vol. 48, no. 10, pp. 2964–2982, Oct. 2015. ↩
6. G. Liu, Z. Lin, S. Yan, J. Sun, Y. Yu, and Y. Ma, “Robust recovery of subspace structures by low-rank representation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 35, no. 1, pp. 171–184, Jan. 2013. ↩
7. J. Wright, A. Y. Yang, A. Ganesh, S. S. Sastry, and Y. Ma, “Robust face recognition via sparse representation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 31, no. 2, pp. 210–227, Feb. 2009. ↩
8. E. J. Candès, X. Li, Y. Ma, and J. Wright, “Robust principal component analysis?” J. ACM, vol. 58, no. 3, p. 11, May 2011. ↩
9. G. Liu, H. Xu, and S. Yan, “Exact subspace segmentation and outlier detection by low-rank representation,” J. Mach. Learn. Res.-Proc. Track, vol. 22, pp. 703–711, 2012. ↩
10. S. Li, M. Shao, and Y. Fu, “Locality linear fitting one-class SVM with low-rank constraints for outlier detection,” in Proc. Int. Joint Conf. Neural Netw., Jul. 2014, pp. 676–683. ↩
11. R. Raina, A. Battle, H. Lee, B. Packer, and A. Y. Ng, “Self-taught learning: Transfer learning from unlabeled data,” in Proc. 24th Int. Conf. Mach. Learn., 2007, pp. 759–766. ↩
12. H. Wang, F. Nie, and H. Huang, “Robust and discriminative self-taught learning,” in Proc. 30th Int. Conf. Mach. Learn., 2013, pp. 298–306. ↩
13. J. Wright, A. Y. Yang, A. Ganesh, S. S. Sastry, and Y. Ma, “Robust face recognition via sparse representation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 31, no. 2, pp. 210–227, Feb. 2009. ↩
14. L. Ma, C. Wang, B. Xiao, and W. Zhou, “Sparse representation for face recognition based on discriminative low-rank dictionary learning,” in Proc. 25th IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2012, pp. 2586–2593. ↩
15. G. Liu, Z. Lin, S. Yan, J. Sun, Y. Yu, and Y. Ma, “Robust recovery of subspace structures by low-rank representation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 35, no. 1, pp. 171–184, Jan. 2013. ↩
16. S. Wang, D. Liu, and Z. Zhang, “Nonconvex relaxation approaches to robust matrix recovery,” in Proc. 23rd Int. Joint Conf. Artif. Intell., 2013, pp. 1764–1770. ↩
17. C.-H. Zhang, “Nearly unbiased variable selection under minimax concave penalty,” Ann. Statist., vol. 38, no. 2, pp. 894–942, 2010. ↩
18. S. Wang, D. Liu, and Z. Zhang, “Nonconvex relaxation approaches to robust matrix recovery,” in Proc. 23rd Int. Joint Conf. Artif. Intell., 2013, pp. 1764–1770. ↩