sklearn聚类算法之Kmeans
基本思想
K-Means聚类是最常见的一种聚类算法。在K-Means聚类中,算法试图把观察值分到k个组中,每个组的方差都差不多。分组的数量k是用户设置的一个超参数。具体来讲,K-Means算有如下几个步骤:
-
随机创建k个分组(即cluster)的“中心“点
-
对于每个观察值:
(1) 算出每个观察值和这k个中心点之间的距离
(2) 将观察值指派到离它最近的中心点的分组
-
将中心点移动到相应分组的点的平均值位置
-
重复步骤2和3,直到没有观察值需要改变它的分组。这时算法就被认为已经收敛,而且可以停止了
关于K-Means算法,有3点值得注意。第一,K-means聚类假设所有的聚类是凸形的(比如,圆形或者球形)。第二,所有特征在同一度量范围内。第三,分组之间是均衡的(即每个分组中观察值的数量大致相等)。如果你认为自己无法满足这些假设,就可能需要尝试其他的聚类方法。
API学习
class sklearn.cluster.KMeans(
n_clusters=8,
*,
init='k-means++',
n_init=10,
max_iter=300,
tol=0.0001,
verbose=0,
random_state=None,
copy_x=True,
algorithm='auto'
)
| 参数 | 类型 | 解释 |
|---|---|---|
| n_clusters | int, default=8 | K-Means中的k,表示聚类数 |
| init | {‘k-means++’, ‘random’}, default=‘k-means++’ | 'k-means++'用一种特殊的方法选定初始质心加速迭代过程收敛,'random’随机选取初始质心 |
| n_init | int, default=10 | 用不同的聚类中心初始化值运行算法的次数,最后的解是inertial意义下选出的最优结果 |
| max_iter | int, default=300 | 运行的最多迭代数 |
| tol | float, default=1e-4 | 容忍的最小误差,当误差小于tol就会退出迭代 |
| verbose | int, default=0 | 是否输出详细信息 |
| random_state | int, RandomState instance or None, default=None | 用于初始化质心得生成器(generator)。如果值为一个整数,则确定一个seed |
| copy_x | bool, default=True | 如果为True,表示计算距离不会修改源数据 |
| algorithm | {“auto”, “full”, “elkan”}, default=“auto” | 优化算法,full表示一般的K-Means算法,elkan表示elkan K-Means算法,auto根据数据是否稀疏进行选择 |
| 属性 | 类型 | 解释 |
|---|---|---|
| cluster_centers_ | ndarray of shape(n_clusters, n_features) | 聚类中心的坐标 |
| labels_ | ndarray of shape(n_samples,) | 分类结果 |
| inertia_ | float | 样本到其最近聚类中心的距离平方和 |
| n_iter_ | int | 运行的迭代次数 |
| n_features_in_ | int | 拟合期间的特征个数 |
| feature_names_in_ | ndarray of shape(n_features_in_,) | 拟合期间的特征名称 |
| 方法 | 说明 |
|---|---|
| fit(X[, y, sample_weight]) | Compute k-means clustering. |
| fit_predict(X[, y, sample_weight]) | Compute cluster centers and predict cluster index for each sample. |
| fit_transform(X[, y, sample_weight]) | Compute clustering and transform X to cluster-distance space. |
| get_params([deep]) | Get parameters for this estimator. |
| predict(X[, sample_weight]) | Predict the closest cluster each sample in X belongs to. |
| score(X[, y, sample_weight]) | Opposite of the value of X on the K-means objective. |
| set_params(**params) | Set the parameters of this estimator. |
| transform(X) | Transform X to a cluster-distance space. |
代码示例
>>> from sklearn.cluster import KMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [10, 2], [10, 4], [10, 0]])
>>> kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
>>> kmeans.labels_
array([1, 1, 1, 0, 0, 0], dtype=int32)
>>> kmeans.predict([[0, 0], [12, 3]])
array([1, 0], dtype=int32)
>>> kmeans.cluster_centers_
array([[10., 2.],
[ 1., 2.]])
优秀作品学习
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
plt.figure(figsize=(12, 12))
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
# Incorrect number of clusters
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
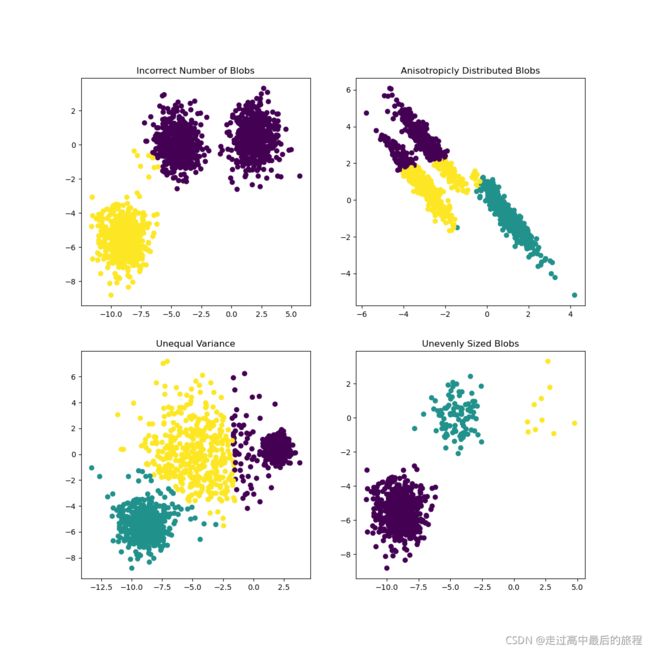
plt.title("Incorrect Number of Blobs")
# Anisotropicly distributed data
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")
# Different variance
X_varied, y_varied = make_blobs(
n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
plt.subplot(223)
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")
# Unevenly sized blobs
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_filtered)
plt.subplot(224)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")
plt.show()