朴素贝叶斯算法代码实现（垃圾邮件检测）

1.文本预处理

（1）分词

首先需要对文本进行分词操作，转换为list,同时词语全部小写，并去除字母数量小于等于2的单词

# 将词切分为list
def textParse(input_string):
    listofTokens = re.split(r'\W+',input_string)
    return [tok.lower() for tok in listofTokens if len(listofTokens)>2]

(2)创建语料表

对于每一封邮件，我们需要得到每一封邮件出现的词语，即语料表

# 创建语料表
def creatVocablist(doclist):
    vocabSet = set([])
    for document in doclist:
        vocabSet = vocabSet|set(document)   # 对语料表中的每个词,取集合的并集
    return list(vocabSet)

 （3）得到词向量

首先初始化一个向量，只要对应词在邮件中出现，相应位置置1，于是我们得到了词向量

# 得到词向量
def setOfWord2Vec(vocablist,inputSet):
    returnVec  = [0]*len(vocablist) # 初始化
    # 只要对应位置的词在语料表中出现了，置为1
    for word in inputSet:
        if word in vocablist:
            returnVec[vocablist.index(word)] = 1
    return returnVec

串联起来：

        首先读取邮件，得到每个邮件的语料表，然后划分训练集和测试集，得到训练集每个邮件的词向量以及类别（垃圾邮件/非垃圾邮件） 

 2.训练模块

        首先，我们回顾一下朴素贝叶斯原理和公式：

问题：给定一封邮件，判定它是否属于垃圾邮件D来表示这封邮件，注意 D 由 N 个单词组成。我们用 h+ 来表示 垃圾邮件，h- 表示正常邮件
P(h+|D) = P(h+) * P(D|h+) / P(D)

P(h- |D) = P(h- ) * P(D|h- ) / P(D)

先验概率：P(h+) 和 P(h-) 这两个先验概率都是很容易求出来的，只需要计算一个邮件库里面垃圾邮件和正常邮件的比例就行了。
D 里面含有 N 个单词 d1, d2, d3，P(D|h+) = P(d1,d2,..,dn|h+) P(d1,d2,..,dn|h+) 就是说在垃圾邮件当中出现跟我们目前这封邮件一 模一样的一封邮件的概率是多大！
 

 P(d1,d2,..,dn|h+) 扩展为： P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1,

h+) * ..
 P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * .. 假设 di 与 di-1 是完全条件无关的（朴素贝叶斯假设特征之间是独 立，互不影响）

简化为 P(d1|h+) * P(d2|h+) * P(d3|h+) * ..
对于P(d1|h+) * P(d2|h+) * P(d3|h+) * ..只要统计 di 这个单词在垃圾邮件中出现的频率即可

同时，对于不同的具体猜测 h+/h-，P(D) 都是一样的，所以在比较P(h+ | D) 和 P(h2-| D) 的时候我们可以忽略这个常数

因此，我们需要得到P(h+)、P(D|h+)、P(D|h- )

对于P(h+)，我们只需要用垃圾邮件数/总邮件数即可。

对于P(D|h+)，我们需要得到垃圾邮件词向量/总的词语数量，对于初始化，我们采用拉普拉斯初始化，即分子用1进行初始化，分母用类别数量进行初始化。最后，由于求得的概率值太小，我们取对数，将数值扩大。

对于P(D|h- )，我们也采取同样的操作

# 朴素贝叶斯算法训练模块
def trainNB(trainMat,trainClass):
    numTrainDocs = len(trainMat) # 总的邮件数
    numWords = len(trainMat[0]) # 总的词语数量
    p1 = sum(trainClass)/float(numTrainDocs) # 垃圾邮件的概率
    p0Num = np.ones((numWords)) #做了一个平滑处理
    p1Num = np.ones((numWords)) #拉普拉斯平滑,分子用1初始化，分母用类别个数初始化
    p0Denom = 2
    p1Denom = 2 #通常情况下都是设置成类别个数
    
    for i in range(numTrainDocs):
        if trainClass[i] == 1: #垃圾邮件
            p1Num += trainMat[i] # 垃圾邮件词语数量
            p1Denom += sum(trainMat[i]) # 分母，垃圾邮件总的词语数量
        else:   # 正常邮件
            p0Num += trainMat[i] #
            p0Denom += sum(trainMat[i])
    p1Vec = np.log(p1Num/p1Denom)
    p0Vec = np.log(p0Num/p0Denom)
    return p0Vec,p1Vec,p1

3.推理模块

        首先我们观察公式，P(h+|D) = P(h+) * P(D|h+)（按照上面所说,P(D)为常数，不考虑），即log(h+|D) = log(P(h+) )+log( P(D|h+)),同理log(h-|D) = log(P(h-) )+log( P(D|h-))。如果log(h+|D)>log(h-|D) ,我们即可认为该邮件为垃圾邮件（正类为垃圾邮件）。

代码如下：（用词向量直接乘以邮件中出现对应词的概率即可直接筛选出出现的词语及其概率）

def classifyNB(wordVec,p0Vec,p1Vec,p1_class):    
    p1 = np.log(p1_class) + sum(wordVec*p1Vec) # 对数形式
    p0 = np.log(1.0 - p1_class) + sum(wordVec*p0Vec)
    if p0>p1:
        return 0
    else:
        return 1

总的代码如下：

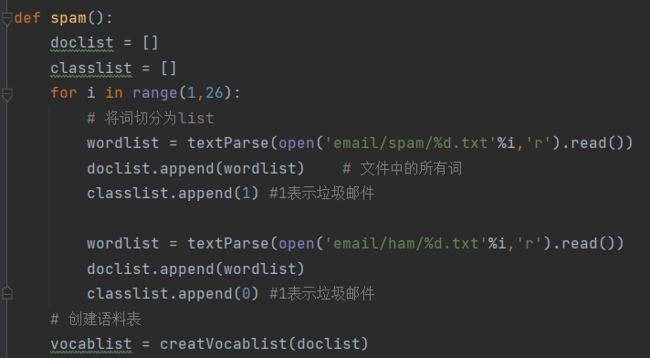
def spam():
    doclist = []
    classlist = []
    for i in range(1,26):
        # 将词切分为list
        wordlist = textParse(open('email/spam/%d.txt'%i,'r').read())
        doclist.append(wordlist)    # 文件中的所有词
        classlist.append(1) #1表示垃圾邮件
        
        wordlist = textParse(open('email/ham/%d.txt'%i,'r').read())
        doclist.append(wordlist)
        classlist.append(0) #1表示垃圾邮件
    # 创建语料表
    vocablist = creatVocablist(doclist)
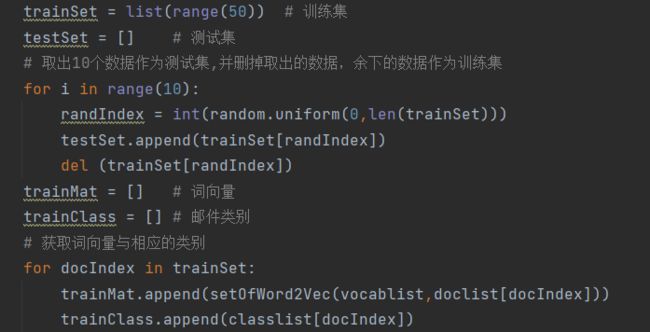
    trainSet = list(range(50))  # 训练集
    testSet = []    # 测试集
    # 取出10个数据作为测试集,并删掉取出的数据，余下的数据作为训练集
    for i in range(10):
        randIndex = int(random.uniform(0,len(trainSet)))
        testSet.append(trainSet[randIndex])
        del (trainSet[randIndex])
    trainMat = []   # 词向量
    trainClass = [] # 邮件类别
    # 获取词向量与相应的类别
    for docIndex in trainSet:
        trainMat.append(setOfWord2Vec(vocablist,doclist[docIndex]))
        trainClass.append(classlist[docIndex])
    p0Vec,p1Vec,p1 = trainNB(np.array(trainMat),np.array(trainClass))
    errorCount = 0
    for docIndex in testSet:
        wordVec = setOfWord2Vec(vocablist,doclist[docIndex])
        if classifyNB(np.array(wordVec),p0Vec,p1Vec,p1) != classlist[docIndex]:
            errorCount+=1
    print ('当前10个测试样本，错了：',errorCount)