数据结构——线性表——栈

目录

一、栈

1.栈的定义

2.栈的分类

二、栈的顺序存储结构

1.顺序栈的定义

2.顺序栈是四要素

3.顺序栈的基本运算算法

(1)代码部分

（2）结果演示

三、栈的链式存储结构

1.链栈的定义

 2.链栈的四要素

3.链栈的基本运算算法

（1）代码部分

（2）结果演示

四、实例讲解

1.判断一个字符串是否为回文。

2.进制转换

五、总结

---

一、栈

1.栈的定义

栈是只能从一端存取数据和读取数据且遵循 "先进后出" 或“后进后出”原则的线性存储结构。

2.栈的分类

与线性表存储结构类似，栈也有两种存储结构：顺序存储结构和链式存储结构。

二、栈的顺序存储结构

1.顺序栈的定义

顺序栈：即用顺序存储结构方式设计栈的存储数据，从而实现栈存储结构。

顺序栈通常有一个一维数组data和一个记录栈顶元素位置的变量top组成，底部称为栈底，头部称为栈顶。如图所示：

2.顺序栈是四要素

设顺序栈为st.

(1)栈空：st.top==-1。

(2)栈满条件:st.top==MaxSize-1。

(3)元素x进栈操作：st.top++;将元素x放在st.data[st.top]中。

(4)出栈元素x操作:取出栈元素x=st.data[st.top];st.top--

3.顺序栈的基本运算算法

a:void InitStack()  //初始化顺序栈

b：void DestroyStack()   //销毁顺序栈

c：int Push()  //进栈操作

d:int Pop()    //出栈操作

e:int GetTop()  //取栈顶元素运算

f:int StackEmpty()  //判断栈是否为空

(1)代码部分

#include
typedef char ElemType;
//顺序栈的声明
#define MaxSize 200     //定义全局变量
typedef struct
{
	ElemType data[MaxSize];
	int top;
}SequenceStack;
//初始化
void InitStack(SequenceStack &st)
{
	st.top=-1;  //设计栈顶
}
//销毁
void DestroyStack(SequenceStack st)
{
}  //由于顺序栈的内存空间是有系统自由分配的，故系统也会自动释放其空间
//进栈
int Push(SequenceStack &st,ElemType x)
{
	if(st.top==MaxSize-1)
		return 0;           //栈满
	else 
	{
		st.top++;
		st.data[st.top]=x;
		return 1;            //成功进栈
	}
}
//出栈

int Pop(SequenceStack &st,ElemType &x)
{
	if(st.top==-1)
	return 0;             //栈空
	else
	{
		x=st.data[st.top];
		st.top--;
		return 1;           //成功出栈
	}
}

//取栈顶元素运算
int GetTop(SequenceStack st,ElemType &x)
{
	if(st.top==-1)
		return 0;         //栈空
	else
	{
		x=st.data[st.top];
		return 1;     //成功去栈顶元素
	}
}
//判断栈空运算算法
int StackEmpty(SequenceStack st)
{
	if(st.top==-1)
		return 1;    //栈空
	else
		return 0;    //栈不空
}

void main()
{
	SequenceStack st;
	ElemType e;
	printf("初始化栈st\n");
	InitStack(st);
	printf("栈%s\n",(StackEmpty(st)==1 ?"空" : "不空"));
	printf("a进栈\n");
	Push(st,'a');
	printf("b进栈\n");
	Push(st,'b');
	printf("c进栈\n");
	Push(st,'c');
	printf("d进栈\n");
	Push(st,'d');
	printf("e进栈\n");
	Push(st,'e');
	printf("f进栈\n");
	Push(st,'f');
	printf("栈%s\n",(StackEmpty(st)==1 ?"空" : "不空"));
	GetTop(st,e);
	printf("栈顶元素:%c\n",e);
	printf("出栈次序:");
	while(!StackEmpty(st))
	{
		Pop(st,e);
		printf("%c",e);
	}
	printf("\n");
	DestroyStack(st);
}

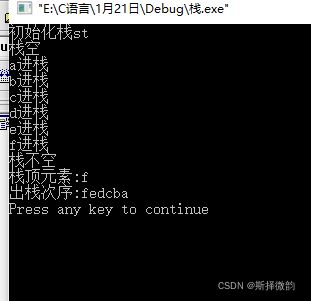
（2）结果演示

三、栈的链式存储结构

1.链栈的定义

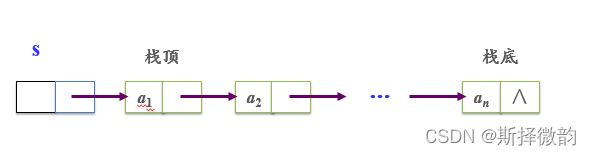
采用链式存储结构存储的栈称为链栈。本文采用单链表存储。如图所示：

 2.链栈的四要素

（1）栈空条件：s->next=NULL

（2）栈满条件：不考虑

（3）进制操作：将包含e结点插入到头结点之后

（4）出栈操作：取出头结点之后结点是元素并删除之。

3.链栈的基本运算算法

（1）代码部分

#include 
#include
typedef char ElemType;
//链栈声明
typedef struct node
{
	ElemType data;
	struct node *next;     //指针域
}LinkStack;
//初始化
void InitStcak(LinkStack *&s)
{
	s=NULL; //空栈
}
//销毁
void DestroyStack(LinkStack *&s)
{
	LinkStack *pre=s,*p;
	if(pre==NULL)       //空栈
		return ;
	p=pre->next;
	while(p!=NULL)
	{
		free(pre);   //释放pre结点
		pre=p;
		p=p->next;
	}
	free(pre);      //释放尾结点
}
//进栈
int Push(LinkStack *&s,ElemType x)
{
	LinkStack *p;
	p=(LinkStack *)malloc(sizeof(LinkStack));
	p->data=x;       //插入p结点作为栈顶结点
	p->next=s;
	s=p;
	return 1;
}
//出栈
int Pop(LinkStack *&s,ElemType &x)
{
	LinkStack *p;
	if(s==NULL)       //栈空返回0
		return 0;
	else               //栈不空
	{
		p=s;           //p指向栈顶结点
		x=p->data;      //取栈顶运算x
		s=p->next;     //删除结点p
		free(p);        
		return 1;
	}
}
//取栈顶元素运算
int GetTop(LinkStack *s,ElemType &x)
{
	if(s==NULL)
		return 0;         //栈空
	else
	{
		x=s->data;    //栈不空
		return 1;
	}
}
//判断栈空
int StackEmpty(LinkStack *s)
{
	if(s==NULL)
		return 1;
	else
		return 0;
}

void main()
{
	ElemType e;
	LinkStack *st;
	printf("初始化st\n");
	printf("栈%s\n",(StackEmpty(st)==1 ?"空":"不空"));
	printf("a进栈\n");
	Push(st,'a');
	printf("b进栈\n");
	Push(st,'b');
	printf("c进栈\n");
	Push(st,'c');
	printf("e进栈\n");
	Push(st,'e');
	printf("d进栈\n");
	Push(st,'d');
	printf("f进栈\n");
	Push(st,'f');
	printf("栈%s\n",(StackEmpty(st)==1 ?"空":"不空"));
	GetTop(st,e);
	printf("栈顶元素:%c\n",e);
	printf("出栈次序:");
	while(!StackEmpty(st))
	{
		Pop(st,e);
		printf("%c",e);
	}
	printf("\n");
	DestroyStack(st);
}

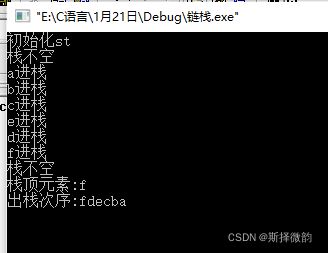
（2）结果演示
 

四、实例讲解

1.判断一个字符串是否为回文。

分析：回文是指一个字符串str从前面度和从后面都一样，将字符串str颠倒输出并保持到另一个字符串str2中，如何通过比较字符串str和字符串str2是否一一对应即可判断是否为回文。

由于顺序栈的特点是先进后出，故将字符串str从头到尾的各个字符依次进栈便可得到一个颠倒后是字符串；然后将字符串str从头到尾的各个字符依次与从栈顶到栈底的各个字符比较即可，如果两者都相同，则str是回文，否则不是。

代码详解

int Palindrome(char str[],int strSize)
{
	SequenceStack st;         //定义一个顺序栈st
	InitStack(st);
	int i;
	char str2;
	for(i=0;i

2.进制转换

本例一十进制转十六进制为例。

分析：采用辗转相除法求余数，并将余数进栈暂存与顺序栈中，最后通过出栈输出十六进制数即可

代码详解：

void tranfroms(int n,char a[])
{
	SequenceStack st;
	InitStack(st);
	char ch;
	int i=0;
	while(a!=0)
	{
		ch='0'+n%2;
		Push(st,ch);
		n/=2;
	}
	while(!StackEmpty(st))
	{
		Pop(st,ch);
		a[i]=ch;
		i++;
	}
	a[i]='\0';
	DestroyStack(st);
}

五、总结

栈是线性表中特殊的存在，具有先进后出、后进先出的特点，可以快速有效的分配存储方式，可以实现很多功能。