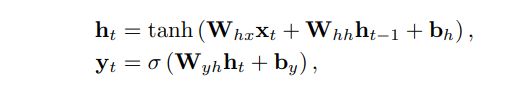DKT学习
《知识追踪综述》
《Deep Knowledge Tracing》
DKT模型
DKT是Deep Knowledge Tracing的缩写,即深度知识追踪,论文中采用了两种模型,一种是带有sigmoid单位的普通RNN模型,另一种是长-短期记忆(LSTM)模型。
0.什么是知识追踪
知识追踪的任务是根据学生的历史学习轨迹来自动追踪学生的知识水平随时间的变化过程,以便能够准确地预测学生在未来学习中的表现。通常,知识追踪的任务可以形式化为:给定一个学生在特定学习任务上的历史学习交互序列 X i = ( x 1 , x 2 , x 3 , . . . , x t ) X_{i} = (x_{1}, x_{2}, x_{3},. . ., x_{t}) Xi=(x1,x2,x3,...,xt),预测该学生在下一个交互 x t + 1 x_{t+1} xt+1的表现,而 x t x_{t} xt通常被表示 ( q t , a t ) (q_{t}, a_{t}) (qt,at),意思是学生在t时刻回答了问题 q t q_{t} qt, 回答的情况是 a t a_{t} at(0或1)。
1. DKT模型概述
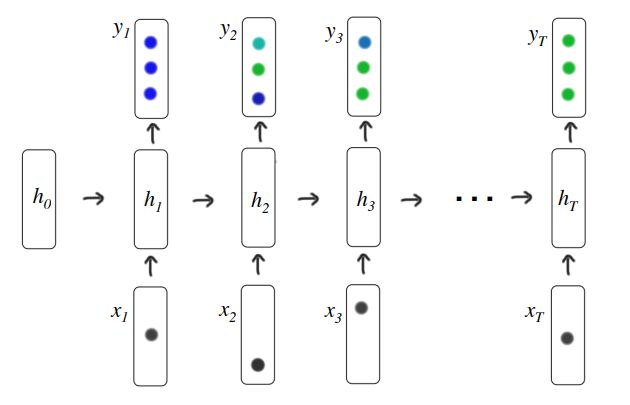
上面的图十分直观:
- 模型的输入是 X = ( x 1 , x 2 , . . . x t , . . . , x T ) X = (x_{1}, x_{2}, ... x_{t}, . . .,x_{T}) X=(x1,x2,...xt,...,xT),代表一个时间序列,该序列中的 x t x_{t} xt是一个one_hot向量,代表学生在t时刻回答的题目以及回答的结果;
- 每当输入一个 X X X,都会得到该时刻对应的输出 Y = ( y 1 , y 2 , . . . y t , . . . , y T ) Y = (y_{1}, y_{2}, ... y_{t}, . . .,y_{T}) Y=(y1,y2,...yt,...,yT),也是一个时间序列, y t y_{t} yt记录的是在t时刻学生答对各个题目的概率;
- 模型的隐层是 H = ( h 1 , h 2 , . . . h t , . . . , h T ) H = (h_{1}, h_{2}, ... h_{t}, . . .,h_{T}) H=(h1,h2,...ht,...,hT),在RNN中,对于每个隐层单元 h t h_{t} ht,其状态更新既受到输入 x t x_{t} xt的影响,也受到上一时刻隐层单元状态 h t − 1 h_{t-1} ht−1的影响。
2. DKT的实现
1. 数据集介绍
数据集是assistment的数据集,分为训练集和测试集:
![]()
训练集和测试集的形式是一样的,打开其中一个文件:

可以看到数据集的形式如下:
题目序列的长度
题目序列
答对的情况
题目序列的长度
题目序列
. . .
数据集的大小:
train: 3134个题目序列
test: 786个题目序列
2. 数据集的处理
首先将数据集保存在一个数组中,该数组名为tuple_rows,每一行表示一个题目序列及其答对的情况:
# 返回值
# tuple_rows的每一行是tup:[[题目个数], [题目序列], [答对情况]],
# max_num_problems最长题目序列
# max_skill_num是知识点(题目)个数
def load_data(fileName):
. . .
with open(fileName, "r") as csvfile:
reader = csv.reader(csvfile, delimiter=',')
for row in reader:
rows.append(row)
index = 0
tuple_rows = []
while(index < len(rows)-1):
...
tup = (rows[index], rows[index+1], rows[index+2])
# tup:[题目个数, 题目序列, 答对情况]
tuple_rows.append(tup)
index += 3
return tuple_rows, max_num_problems, max_skill_num+1
下面将tuple_rows转换成模型需要的输入形式:
input_data:1个batch中输入到rnn网络的数,input_data相当于上面的batch_size个 X = ( x 1 , x 2 , . . . x t , . . . , x T ) X = (x_{1}, x_{2}, ... x_{t}, . . .,x_{T}) X=(x1,x2,...xt,...,xT);
- shape:(num_steps-1, batch_size, input_size)
- 说明: num_steps是最长题目序列长度,batch_size是一个批次的大小,input_size = num_skills*2, 是题号及其答对情况的one_hot编码;
- 值得注意的是:x是答题序列的前n-1个
target_id:1个batch训练结束后用于判断准确率的的题号
- shape:( (num_steps-1)* batch_size)
- 说明:每当向模型中输入一个batch的数据,会得到在不同时刻各个题目的做对的概率 o u t p u t = b a t c h s i z e ∗ Y output = batchsize * Y output=batchsize∗Y,其中 Y = ( y 1 , y 2 , . . . y t , . . . , y T ) Y = (y_{1}, y_{2}, ... y_{t}, . . .,y_{T}) Y=(y1,y2,...yt,...,yT), y t y_{t} yt表示在t时刻学生答对各个题目的概率;此时我们需要判断 Y Y Y是否合理,判断的方法就是对于 y t y_{t} yt,输入 t + 1 t+1 t+1时刻的题号来观察是否预测正确,因此这里的
target_id是题目序列的后n-1个。
target_correctness:与上面的target_id一一对应,表示是否答对。
students, num_steps, num_skills = load_data(...)
x = np.zeros((num_steps, batch_size))
# input_data:(num_steps, batch_size, input_size)
input_data = torch.FloatTensor(num_steps, batch_size, input_size)
input_data.zero_()
# target_id: (num_steps-1)* batch_size
target_id: List[int] = []
# target_correctness: (num_steps-1)* batch_size
target_correctness = []
for i in range(batch_size):
# student: [[题目个数], [题目序列], [答对情况]]
student = students[index+i]
problem_ids = student[1]
correctness = student[2]
# 答题序列的前n-1个作为模型的输入
for j in range(len(problem_ids)-1):
problem_id = int(problem_ids[j])
# 答对就是124+题号, 答错就是题号, 方便后面转化成one_hot
if(int(correctness[j]) == 0):
label_index = problem_id
else:
label_index = problem_id + num_skills
x[j, i] = label_index
# 需要预测的是答题序列的后n-1个(t时刻需要预测t+1时刻)
target_id.append(j*batch_size*num_skills+i*num_skills+int(problem_ids[j+1]))
target_correctness.append(int(correctness[j+1]))
actual_labels.append(int(correctness[j+1]))
x = torch.tensor(x, dtype=torch.int64)
x = torch.unsqueeze(x, 2)
# scatter_用于生成one_hot向量,并且会将所有答题序列长度统一为num_steps
input_data.scatter_(2, x, 1)
3. 定义DKT网络模型
这里主要定义了rnn网络和decoder 网络:
- 隐层(rnn):采用torch.nn.LSTM或者torch.nn.RNN;
- 输出层(decoded):是隐层(self.rnn)到输出层的网络,采用的是一个普通的全连接层。
class DeepKnowledgeTracing(nn.Module):
def __init__(self, input_size, hidden_size, num_skills, nlayers, dropout=0.6, tie_weights=False):
super(DeepKnowledgeTracing, self).__init__()
self.rnn = nn.LSTM(input_size, hidden_size, nlayers, batch_first=True, dropout=dropout)
# self.rnn = nn.RNN(input_size, hidden_size, nlayers, nonlinearity='tanh', dropout=dropout)
# nn.Linear是一个全连接层,hidden_size是输入层维数,num_skills是输出层维数
# decoder是隐层(self.rnn)到输出层的网络
self.decoder = nn.Linear(hidden_size, num_skills)
self.nhid = hidden_size
self.nlayers = nlayers
# 前向计算, 网络结构是:input --> hidden(self.rnn) --> decoder(输出层)
# 这里需要注意:在pytorch中,rnn的输入格式已经和tensorflow的rnn不太一样,具体见官网:
# https://pytorch.org/docs/stable/generated/torch.nn.RNN.html?highlight=rnn#torch.nn.RNN
# 根据官网,torch.nn.RNN接收的参数input形状是[时间步数, 批量大小, 特征维数], hidden: 旧的隐藏层的状态
def forward(self, input, hidden):
# output: 隐藏层在各个时间步上计算并输出的隐藏状态, 形状是[时间步数, 批量大小, 隐层维数]
output, hidden = self.rnn(input, hidden)
# decoded: 形状是[时间步数, 批量大小, num_skills]
decoded = self.decoder(output.contiguous().view(output.size(0) * output.size(1), output.size(2)))
return decoded, hidden
4. 前向计算与反向传播
# 训练
if training:
# 前向计算, output:(num_steps, batch_size, num_skills)
output, hidden = model(input_data, hidden)
# 将输出层转化为一维张量
output = output.contiguous().view(-1)
# tf.gather用一个一维的索引数组,将张量中对应索引的向量提取出来
logits = torch.gather(output, 0, target_id)
# 计算误差,相当于nn.functional.binary_cross_entropy_with_logits()
criterion = nn.BCEWithLogitsLoss()
loss = criterion(logits, target_correctness)
# 反向传播
loss.backward()
# 梯度截断,防止在RNNs或者LSTMs中梯度爆炸的问题
torch.nn.utils.clip_grad_norm_(m.parameters(), args.max_grad_norm)
optimizer.step()
5. 完整代码
https://github.com/YAO0747/study/tree/master/DKT
6. 运行结果
训练策略:
- 每个batch输入32条数据,每次迭代需要输入97个batch;
- 每迭代5次训练集,就在测试集上面进行一次测试;
。。。电脑实在是太不给力,150次迭代跑了好几个小时都没跑完,下面记录是当前的运行结果,从结果中可以看到效果还不错,暂时能够达到大约80%的准确率,并且目前准确率一直在上升,说明模型应该是没有什么大问题的:
filename: data/0910_b_train.csvthe number of rows is 10116
tuple_rows 3134
max_num_problems 1219
max_skill_num 124
filename: data/0910_b_test.csvthe number of rows is 2532
tuple_rows 786
max_num_problems 1062
max_skill_num 124
D:\Python_Install\lib\site-packages\torch\nn\modules\rnn.py:50: UserWarning: dropout option adds dropout after all but last recurrent layer, so non-zero dropout expects num_layers greater than 1, but got dropout=0.6 and num_layers=1
"num_layers={}".format(dropout, num_layers))
0.4911625932282999 0.5269459839244541 -0.068528311726332
0.4770511049811472 0.5550040623596215 -0.008011016759000178
0.47077620987256746 0.5833168318034264 0.01833234265021122
0.4695175454496687 0.5921604046011325 0.02357448699124831
0.46909517161498243 0.5951040826348157 0.02533046433033237
Testing
0.46874281802812096 0.5843573741705338 0.01988331550332434
0.46881151261820625 0.5971281076645534 0.0265088614164396
0.46855559722559087 0.5990175204711764 0.027571392357636282
0.46829880824927506 0.6009425516721646 0.028636967168644722
0.46802999716506716 0.6029348116708813 0.029751803268299848
0.4677428253065596 0.6050428501896573 0.03094207953208805
Testing
0.4674941950638955 0.5937275598579316 0.025097971375143358
0.4674323391332927 0.6072677036039826 0.03222816756100233
0.46709388450915085 0.6096316444776071 0.03362913296563752
0.4667227211497568 0.612154178344099 0.03516432304678663
0.46631387014006753 0.6148563700209385 0.03685398263438888
0.4658620399021397 0.6177745977277902 0.03871954011006129
Testing
0.46556671679919787 0.6072288920955657 0.03312043976532786
0.4653615729428706 0.6209614494378694 0.040783802295099036
0.4648063844212343 0.6243916909226939 0.04307117702964669
0.46418988992581417 0.628069417692588 0.045607932711993704
0.46350499858731975 0.6319594928622866 0.04842218030933099
0.46274451259755833 0.6360292840527009 0.051542180896336776
Testing
0.462337976528247 0.6260747342032811 0.046484702680089085
0.4619029277800827 0.6402607780416857 0.05498892887986506
0.4609823956117148 0.6446793192634664 0.05875182453512218
0.45999983762800684 0.6491738144873334 0.06275998322308762
0.4589538434125271 0.6537803413039093 0.06701751963547564
0.4578529388069752 0.658623468678053 0.07148809038582604
Testing
0.45737519449362146 0.6502498791987154 0.06684509473254985
0.4567160157984641 0.6635986497020953 0.07609365603217855
0.45551905157905326 0.6687523695661212 0.08093006923097623
0.45423916490603605 0.674121607306376 0.0860874948104754
0.45286155438207665 0.6796807774284296 0.09162249231621455
0.45137396238112787 0.685390064006621 0.09758049729955698
Testing
0.45070536358083246 0.6798890971889712 0.09386275465371408
0.4497697584329197 0.6911855926751093 0.10398357995623775
0.44805308972829366 0.6970611647429005 0.11081030811567572
0.4462492676198428 0.7029009923504653 0.11795549426075247
0.44440893611136045 0.708537398359284 0.12521559422656225
0.4425862160930401 0.7137755471998872 0.1323766437293291
Testing
0.44196702576424873 0.7075558066524807 0.12865876579649915
0.440821958008921 0.7185326424010529 0.13927997947469928
0.4391459127619552 0.7228192659216532 0.1458126088687608
0.4375791673872718 0.7266961465601469 0.15189672251972097
0.43613170190713724 0.7301914875454761 0.15749831383583968
0.4348024170696389 0.7333597382241634 0.16262620526898508
Testing
0.43499610416425966 0.7256302408654163 0.15592844707974907
0.43358353475999456 0.7362444605662153 0.1673144473573157
0.43246859811511945 0.7388764175284888 0.17159135322429797
0.43145399856058425 0.7412553263797625 0.17547379514102468
0.4305301716634814 0.7434221642644268 0.17900095675359484
0.42971015564566084 0.7453295142189681 0.18212543568247708
Testing
0.43031500942684103 0.7384982193572206 0.17399720257874918
0.428987136718106 0.7470821344608052 0.1848753883987937
0.4282981446256455 0.7487294168607489 0.1874916132782526
0.42749546560635593 0.7506722082351938 0.1905342241816368
0.4267802557326967 0.7523348171805027 0.193240468684717
0.4260945372130349 0.753964885001833 0.19583086744835831
Testing
0.42745039293425957 0.7456707881349836 0.18495803510586617
0.4254409154544933 0.7555138478148216 0.19829613864420137
0.42481446821121593 0.7569777740762715 0.20065536363135172
0.4242169368452725 0.7583722773079833 0.2029024508453222
0.42364552862683585 0.7596876874908746 0.20504834036377573
0.423106750827598 0.7609151459510743 0.20706903892751438
Testing
0.4250698062704704 0.7515114327228813 0.1940111327185461
0.42260625671033897 0.7620536202186893 0.20894384975886615
0.4221354049784206 0.7631531495086519 0.2107055968057714
0.4216796576305961 0.764186996243502 0.21240895855272712
0.4212422022130744 0.765171294645951 0.21404222327781586
0.42081885188347284 0.7661292089104378 0.215621211716028
Testing
0.42263162257984976 0.7575863627083204 0.20323085556730947
0.4204002772076461 0.7670773507952541 0.21718082726301424
0.4199764326264256 0.7680397696388412 0.21875849705253858
0.4195649951286688 0.7689639144862466 0.22028846195438345
0.4191812068718538 0.7698075852659262 0.22171425901485864
0.4188225264713298 0.7705858498369136 0.2230455992763608
Testing
0.4209640595587447 0.7612796165543753 0.2095060203270852
0.4184707496492729 0.771358281144888 0.2243502080388693
0.41816423041500034 0.7720559235751017 0.225486079575825
0.41780144471493535 0.772862055459775 0.22682938284629395
0.41741990218418135 0.7737196291100091 0.22824088000433296
0.41713577244970124 0.77433361899622 0.2292911657379494
Testing
0.4201866748819594 0.7630470716562708 0.21242289878681853
0.4168855080695434 0.7748411234404531 0.23021567579478475
0.41660244599079843 0.7755618851337658 0.23126067626451985
0.4163348676169401 0.7761178595242773 0.23224786182501744
0.41616157750105726 0.7764365732095355 0.23288684827111494
0.415826147084532 0.7772465251411171 0.2341229517436375
Testing
0.4198665911773206 0.7629881939862795 0.21362233986551804
0.4155413161680101 0.7779068953776196 0.23517180714115327
0.41529735554019687 0.7784486026582554 0.23606959124477855
0.4150650560089809 0.7789621095287708 0.23692397204698112
0.4147838158620516 0.7795771795671134 0.2379577131634908
0.4144943927089212 0.7802031863283329 0.23902080061130104
Testing
0.4187109285432763 0.765884955074609 0.2179453157843415
0.41420852822868126 0.7808254808710681 0.24007008819034759
0.4139177580657468 0.7814507368747646 0.24113663980217193
0.41365206963885864 0.7820208356001302 0.24211053618351386
0.4134184191404299 0.7825344973360352 0.2429664789043794
0.4131725615370511 0.7830772187472419 0.24386661830588852
Testing
0.4181513935877232 0.7673240662695555 0.22003408167709626
0.4129307812386361 0.7835809611511645 0.24475130756612617
0.41269056665529064 0.7840746864133847 0.24562975494229322
0.41242881299820267 0.7846317139564698 0.2465863871797903
0.41213503016543385 0.7852778236716682 0.24765935369224013
0.4118743339375407 0.785839989043866 0.24861083960057706
Testing
0.4173820649996592 0.768909646388457 0.2229014550352164
0.41163764236182443 0.7863648312118665 0.24947419217172606
0.4114523306384477 0.7868417414210098 0.250149785998271
0.4112915712533774 0.7872451218827268 0.25073562256324466
0.4110598965140879 0.7876906568054132 0.2515794849337024
0.41085369713477743 0.7880510005489033 0.2523301548013054
Testing
0.41701273115875587 0.769642101152134 0.22427612745161962
0.4106685004060979 0.7884437464790234 0.2530040433553383
0.41044182775392174 0.788981145445271 0.2538284397946162
0.41028141512273886 0.7893033719937861 0.254411577013971
0.4101744198031675 0.789602001200235 0.25480040315449504
0.4100383826590607 0.7899611869173964 0.2552946222438617
Testing
0.41697498358294494 0.7697970615682401 0.22441655659550253
0.40983739270901604 0.7903463963029482 0.25602451299962636
0.4097417908274387 0.7905217004260655 0.25637156362033175
0.40966376333800747 0.7906964310717768 0.2566547562871768
0.40946425224055255 0.7911280708671783 0.2573786158292375
0.4091182805311867 0.7919995382183055 0.25863302299706104
Testing
0.4167482477486145 0.7700545517106594 0.2252597954224882
0.40888649279271644 0.7924998115016513 0.2594728343908108
0.40891680393977886 0.7924524057115401 0.259363038346205
0.408892239797739 0.7925291712626074 0.25945201764423986
0.4086393274178546 0.793050438281578 0.26036783756425697
0.4083036493333403 0.7937076151326131 0.2615824848895367
Testing
0.4166151309397987 0.7697418235788674 0.22575464800229939
0.4080097897776851 0.7942730214027083 0.26264499294253685
0.4078889005279916 0.7945546483591439 0.26308187014694795
0.40778883381481285 0.7948362944360214 0.2634433996206095
0.40777169344367076 0.7948582756083145 0.26350531690290835
0.4075254806846342 0.795486636085726 0.2643944401351348
Testing
0.41678584609511393 0.7694134999471642 0.22511999752388023
0.40730073372242676 0.7960246317931496 0.26520557727906013
0.4070979487514321 0.7964327921275742 0.2659370671112392
0.40717303718776476 0.7961537215368437 0.2656662491357362
0.40703480934021713 0.796391458283362 0.2661647504355744
0.4066771258225183 0.7972176977747678 0.2674539052666792
Testing
0.41705967917543685 0.7685028027573768 0.2241014529410975
0.4063193901265356 0.7979550912637798 0.26874211456147146
0.406161924485 0.7982633062642742 0.2693087903467828
0.4057918568783526 0.7990527310941027 0.27063969776724695
0.40555406313401254 0.7995908224037351 0.2714942565624947