R语言学习笔记8_回归分析和相关分析
目录
- 八、回归分析和相关分析
-
- 8.1 相关性及其度量
-
- 8.1.1 相关性概念
- 8.1.2 相关分析
- 8.2 一元线性回归分析
-
- 8.2.1 数学模型
- 8.2.2 估计与检验
- 8.2.3 预测与控制
- 8.3 多元线性回归
-
- 8.3.1 数学模型
- 8.3.2 估计与检验
-
- 回归方程显著性检验
- 回归系数显著性检验
- 8.3.3 预测与控制
- 8.3.4 逐步回归法 step()
- 8.4 回归诊断
-
- 8.4.1 残差分析
-
- 残差及残差图
- 方差齐性的诊断及修正方法
- 异常点的识别
- 8.4.2 影响分析
-
- 影响函数
- Cook距离
- DFFITS准则
- COVRATIO准则
- 影响分析的概括函数 influen.mesures(model)
- 8.4.3 共线性诊断
-
- 特征值法
- 条件指数
- 方差膨胀因子VIF
- 8.5 Logistic回归
-
-
- Logistic回归
- 广义线性模型
-
八、回归分析和相关分析
8.1 相关性及其度量
8.1.1 相关性概念
相关关系是指两个变量的数值变化存在不完全确定的依存关系,它们之间的数值不能用方程表示出来,但可用某种相关性度量来刻画。
| 划分标准 | 种类 |
|---|---|
| 相关程度 | 完全相关、不完全相关、不相关 |
| 相关方向 | 正相关、负相关 |
| 相关形式 | 线性相关、非线性相关 |
| 涉及变量的多少 | 一元相关、多元相关 |
| 影响因素 | 单相关、复相关 |
8.1.2 相关分析
cor.test(x, y,
alternative = c("two.sided", "less", "greater"),
method = c("pearson", "kendall", "spearman"),
exact = NULL, conf.level = 0.95, continuity = FALSE, ...)
x, y是长度相同的向量; alternative是备择假设,默认为two.sided;method是选择检验方法。
cor.test(formula, data, subset, na.action, ...)
formula是公式,必须是具有相同长度的数值向量;data是数据框;subset是可选择向量,表示观察值的子集。
例:对以下数据进行相关性检验:
1.21 1.30 1.39 1.42 1.47 1.56 1.68 1.72 1.98 2.10 3.90 4.50 4.20 4.83 4.16 4.93 4.32 4.99 4.70 5.20
> test<-data.frame(x<-c(1.21,1.30,1.39,1.42,1.47,1.56,1.68,1.72,1.98,2.10),y<-c(3.90,4.50,4.20,4.83,4.16,4.93,4.32,4.99,4.70,5.20))
> cor.test(x,y)
Pearson's product-moment correlation
data: x and y
t = 2.6, df = 8, p-value = 0.03
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.08943 0.91723
sample estimates:
cor
0.6807
由于p=0.03<0.05,故认为变量x与y相关。
8.2 一元线性回归分析
函数关系可以刻画变量之间的因果关系。
8.2.1 数学模型
设变量X和Y之间存在一定的相关关系,回归分析方法即找出Y的值是如何随X的值变化而变化的规律,称Y为因变量(响应变量),X为自变量(解释变量)。
Y=β0+β1X+ε
Y=β0+β1X表示Y随X变化而线性变化的部分,ε是随机误差(其他一切不确定因素影响的总和),通假定ε~ N(0,σ2),f(X)=β0+β1X为一元线性回归函数,β0为回归常数,β1为回归系数,统称回归参数。
8.2.2 估计与检验
- β0、β1的估计(最小二乘估计)
- 回归方程的显著性检验:
H0:β1=0,H1:β1≠0 t检验法、F检验法、相关系数检验法
当拒绝H0时,认为线性回归方程是显著的。
-在R中,函数lm()求回归方程,confint()求参数的置信区间
lm(formula, data, subset, weights, na.action,
method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
singular.ok = TRUE, contrasts = NULL, offset, ...)
formula是回归模型;data是数据框;subset是样本观察的子集;weights用于拟合的加权向量;na.action显示数据是否包含缺失值;method指出用于拟合的方法;model, x, y , qr为T时返回其值。除了formula必选,其他都是可选。
confint(object, parm, level = 0.95, ...)
object指回归模型;parm要求指出所求区间估计的参数,默认为所有的回归参数;level置信水平。
例:有10个同类企业的生产性固定资产价值X和工业总产值Y资料如下。现试确定X与Y之间的关系,求出回归方程,并作检验。
企业编号 生产性固定资产价值(万元) 工业总产值(万元) 1 318 524 2 910 1019 3 200 638 4 409 815 5 415 913 6 502 928 7 314 605 8 1210 1516 9 1022 1219 10 1225 1624
> x<-c(318,910,200,409,425,502,314,1210,1022,1225)
> y<-c(524,1019,638,815,913,928,605,1516,1219,1624)
> lm.reg<-lm(y~1+x)
> summary(lm.reg)#提取模型计算结果
Call:
lm(formula = y ~ 1 + x)
Residuals:
Min 1Q Median 3Q Max
-191.5 -86.6 45.3 79.3 138.2
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 393.043 79.651 4.93 0.0011 **
x 0.898 0.106 8.50 2.8e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 125 on 8 degrees of freedom
Multiple R-squared: 0.9, Adjusted R-squared: 0.888
F-statistic: 72.2 on 1 and 8 DF, p-value: 2.82e-05
#对误差项独立同正态分布的假设进行检验
> par(mfrow=c(2,2))
> plot(lm.reg)
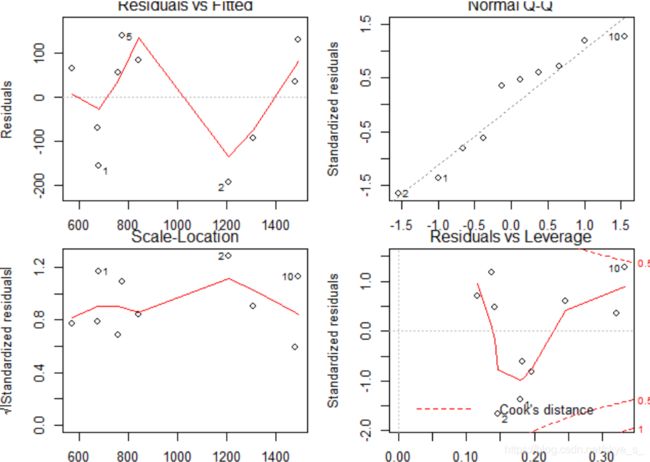
从p值可以看出回归方程Y=393.043+0.898X通过检验。下图:
1)Residual vs Fitted是拟合值y对残差的图形。可以看出数据点都基本均匀的分布在直线y=0的两侧,无明显趋势。
2)Normal QQ中的数据点分布趋于一条直线,说明残差是服从正态分布的。
3)Scale Lcation 显示了标准化残差的平方根分布情况。最高点为残差最大值点。
4)Cook距离图显示了对回归的影响点。
8.2.3 预测与控制
对于X=x0,预测置信水平1-α下Y的取值区间。
控制可以看作预测的反问题:要求观察值Y在某一区间内取值时,应将X控制在什么范围内。
例1:求上例中X=x0=425时相应的Y在置信水平为0.95的预测区间。
> point<-data.frame(x=425)
> point
x
1 425
> lm.pred<-predict(lm.reg,point,interval = "prediction",level=0.95)
> lm.pred
fit lwr upr
1 774.8 466.6 1083
选项interval = "prediction"表示同时要给出相应的预测区间。
由计算结果,当x=425时,y的预测值为774.8,预测区间为[466.6, 1083]。
例2:下表是有关15个地区某种食物年需求量(X,单位:10吨)和地区人口增加量(Y,单位:千人)的资料。利用此表数据展示一元回归模型的统计分析过程。
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 X 274 180 375 205 86 265 98 330 195 53 430 372 236 157 370 Y 162 120 223 131 67 169 81 192 116 55 252 234 144 103 212
> #建立数据集,并画出散点图:考查数据点的分布趋势,看是否呈直线条状分布
> x<-c(274,180,375,205,86,265,98,330,195,53,430,372,236,157,370)
> y<-c(162,120,223,131,67,169,81,192,116,55,252,234,144,103,212)
> A<-data.frame(x,y)
> plot(x,y)
> #进行回归分析,并在散点图上显示回归直线
> lm.reg<-lm(y~x)
> summary(lm.reg)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-9.961 -4.608 -0.262 3.150 14.215
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 22.5959 3.9274 5.75 6.7e-05 ***
x 0.5301 0.0147 36.01 2.1e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.44 on 13 degrees of freedom
Multiple R-squared: 0.99, Adjusted R-squared: 0.989
F-statistic: 1.3e+03 on 1 and 13 DF, p-value: 2.08e-14
> abline(lm.reg)
结论:
- 回归参数的估计与检验:回归参数的估计为β0=22.5959,β1=0.5301,相应的标准差分别为3.9274, 0.0147 ,它们的p值都很小,故是非常显著的。
- 相关分析:相关系数的平方R2=0.99,表明数据中99%可由回归方程来描述。
- 方程的检验:F分布的p值为2.08x10-14,因此方程是非常显著的。
> #计算回归方程的残差,并画出关于残差的散点图。
> res<-residuals(lm.reg)
> plot(res)
> text(12,res[12],labels = 12,adj=(.05))

从上图可以看出,第12个样本点可能有问题(图中已标记,它比其他样本点的残差大很多)或由于模型的假设不正确、σ2不是常数,异常点等等。
8.3 多元线性回归
8.3.1 数学模型
Y=β0+β1X1+β2X2+…+βpXp
对n个观测值可写为:
y1=β0+β1X11+β2X12+…+βpX1p+ε1 ,
y1=β0+β1X21+β2X22+…+βpX2p+ε2 ,
…
y1=β0+β1Xn1+β2Xn2+…+βpXnp+εn
8.3.2 估计与检验
回归方程显著性检验
H0:β0=β1=…=βP=0,H1:β0, β1…βP不全为0
回归系数显著性检验
H0j:βj=0,H1j:βj≠0
例:某公司在各地区销售一种特殊的化妆品,该公司观测了15个城市在某月对该化妆品的销售量Y,使用该化妆品的人数X1和人均收入X2,数据如下。试建立Y与X1,X2的线性回归方程,并作相应的检验。
地区i 销售量Y/箱 人数X1/千人 人均收入X2/元 1 162 274 2450 2 120 180 3250 3 223 375 3802 4 131 205 2838 5 67 86 2347 6 167 265 3782 7 81 98 3008 8 192 330 2450 9 116 195 2137 10 55 53 2560 11 252 430 4020 12 232 372 4427 13 144 236 2660 14 103 157 2088 15 212 370 2605
> y<-c(162,120,223,131,67,169,81,192,116,55,252,232,144,103,212)
> x1<-c(274,180,375,205,86,265,98,330,195,53,430,372,236,157,370)
> x2<-c(2450,3250,3802,2838,2347,3782,3008,2450,2137,2560,4020,4427,2660,2088,2605)
> sales<-data.frame(y,x1,x2)
> lm.reg<-lm(y~x1+x2,data=sales)
> summary(lm.reg)
Call:
lm(formula = y ~ x1 + x2, data = sales)
Residuals:
Min 1Q Median 3Q Max
-3.831 -1.206 -0.244 1.482 3.302
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.445728 2.426693 1.42 0.18
x1 0.495972 0.006046 82.04 < 2e-16 ***
x2 0.009205 0.000967 9.52 6.1e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.17 on 12 degrees of freedom
Multiple R-squared: 0.999, Adjusted R-squared: 0.999
F-statistic: 5.7e+03 on 2 and 12 DF, p-value: <2e-16
由于F检验统计量的p<2e-16,用于回归系数检验的t统计量的p< 2e-16 和 =6.1e-07,均小于0.05,故回归方程与回归系数的检验都是显著的。回归方程为Y=3.445728+0.495972X1+0.009205X2
8.3.3 预测与控制
当多元线性回归方程经过检验是显著的,且其中每一个回归系数均显著时(不显著的先剔除),可以用此方程做预测。
求上例中X=x0=(200,3000)时相应Y的预测值与0.95的预测区间
> pre<-data.frame(x1=200,x2=3000)
> lm.pred<-predict(lm.reg,pre,interval = "prediction",level=0.95)
> lm.pred
fit lwr upr
1 130.3 125.3 135.2
由此求得y0=130.3 ,相应的Y的0.95的预测区间为[125.3, 135.2]
8.3.4 逐步回归法 step()
若回归方程系数的显著性不高,说明变量的选择存在问题,可以用step()函数,通过选择最小的AIC信息统计量来达到删除或增加变量的目的。
step(object, scope, scale = 0,
direction = c("both", "backward", "forward"),
trace = 1, keep = NULL, steps = 1000, k = 2, ...)
object是线性模型或广义线性模型分析的结果(lm.reg);scope是确定逐步搜索的区域;direction 确定逐步搜索的方向,both向前向后,backward向后法,forward向前法。
8.4 回归诊断
8.4.1 残差分析
残差及残差图
1)残差
residuals(object, ...)
resid(object, ...)
2)标准化残差
rstandard(model, infl = lm.influence(model, do.coef = FALSE),
sd = sqrt(deviance(model)/df.residual(model)), type = c("sd.1", "predictive"), ...)
3)学生化残差
rstudent(model, infl = lm.influence(model, do.coef = FALSE),
res = infl$wt.res, ...)
object 或 model 是由线性模型函数 lm() 或广义线性模型函数 glm() 生成的对象,infl是由lm.influence()返回值得到的影响结构,sd是模型的标准差,res是模型的残差。
凡是以残差为纵坐标,以观测值、预测值、自变量或序号、观测时间等为横坐标的散点图,均称为残差图。
计算8.3.2例的残差和标准残差,并画出相应的残差散点图。
> y.res<-residuals(lm.reg)#计算残差
> print(y.res)
1 2 3 4 5 6 7 8 9 10 11 12
0.1058 -2.6367 -1.4324 -0.2436 -0.7032 -0.6913 1.2607 2.3314 -3.8312 1.7032 -1.7175 3.3025
13 14 15
-0.9802 2.4668 1.0657
> y.rst<-rstandard(lm.reg)#计算标准化残差
> y.rst
1 2 3 4 5 6 7 8 9 10 11
0.05281 -1.30636 -0.73053 -0.11643 -0.36046 -0.35064 0.66372 1.23228 -1.92771 0.91559 -0.93262
12 13 14 15
1.89069 -0.47083 1.24504 0.57928
> y.fit<-predict(lm.reg)#计算预测值
> par(mfrow=c(1,2))
> plot(y.res~y.fit)
> plot(y.rst~y.fit)
方差齐性的诊断及修正方法
当残差的绝对值随预测值的增加也有明显增加(减少,或先增加后减少)的趋势时,表示关于误差的方差齐性假定不成立。
误差的方差非齐性时,有时可以通过对因变量作适当的变换,令Z=f(x),使得关于因变量Z在回归中误差的方差接近齐性。常见的方差稳定性变换有:
1)开方变换:Z=√Y(Y>0);
2)对数变换:Z=ln(Y) (Y>0);
3)倒数(逆)变换:Z=1/Y(Y≠0);
4)BOX-COX变换:Z=(Xλ-1)/λ,λ=0时为对数变换。
例:在对27家企业单位的研究中,记录了企业管理人数Y与工人X的资料。试建立Y对X的回归方程。
序号 X Y 序号 X Y 序号 X Y 1 294 50 10 697 78 19 700 106 2 247 40 11 688 80 20 850 128 3 267 45 12 630 84 21 980 130 4 358 55 13 709 88 22 1025 160 5 423 70 14 627 97 23 1021 97 6 311 65 15 615 100 24 1200 180 7 450 55 16 999 109 25 1250 112 8 534 62 17 1022 114 26 1500 210 9 438 68 18 1015 117 27 1650 135
> x<-c(294,247,267,358,423,311,450,534,438,697,688,630,709,627,615,999,1022,1015,700,850,980,1025,1021,1200,1250,1500,1650)
> y<-c(50,40,45,55,70,65,55,62,68,78,80,84,88,97,100,109,114,117,106,128,130,160,97,180,112,210,135)
> persons<-data.frame(x,y)
> #做线性回归模型
> lm.reg<-lm(y~x)
> summary(lm.reg)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-47.65 -11.14 -4.28 11.68 41.68
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 25.0943 9.2754 2.71 0.012 *
x 0.0955 0.0110 8.69 5e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 21.1 on 25 degrees of freedom
Multiple R-squared: 0.751, Adjusted R-squared: 0.741
F-statistic: 75.5 on 1 and 25 DF, p-value: 5.02e-09
> #回归系数、回归方程均通过检验,回归方程为Y=25.0943+0.0955X
> #回归诊断:画出标准化残差散点图
> y.rst<-rstandard(lm.reg)
> y.fit<-predict(lm.reg)
> plot(y.rst~y.fit)
> #模型更新
> lm.new<-update(lm.reg,sqrt(.)~.)
> coef(lm.new)
(Intercept) x
6.044644 0.004781
> yn.rst<-rstandard(lm.new)
> yn.fit<-predict(lm.new)
> plot(yn.rst~yn.fit)
图形如下图(左)所示,容易看出残差图从左向右逐渐散开,这是方差齐性不成立的典型征兆,因此考虑对响应变量做Y变换,得到右图,趋势大有改善。更新后的回归方程为Y=(6.044644 + 0.004781X)2

异常点的识别
如果拟合后的模型能够很好的描述这组数据,那么残差对预测值的散点图应该像一些随机分布的点。
如果出现了一小部分残差绝对值很大的点那么这些观测值很可能是异常点,它们不能用来与其他数据一起拟合模型。
一般把标准化残差绝对值≥2的观测点认为是可疑点;标准化残差绝对值≥3的观测点认为是异常点。
8.4.2 影响分析
找出对回归结果影响很大的观测点
影响函数
lm.influence(model, do.coef = TRUE)
model是回归模型;do.coef = TRUE表示结果要求给出去掉第i个观测点后的模型回归系数。
Cook距离
是从估计角度提出的一种度量第i个观测点对回归影响大小的统计量。当距离的绝对值>4/n时认为是强影响点。
cooks.distance(model, infl = lm.influence(model, do.coef = FALSE),
res = weighted.residuals(model),
sd = sqrt(deviance(model)/df.residual(model)),
hat = infl$hat, ...)
DFFITS准则
统计量i的绝对值>2√(p+1)/n则认为第i个样本的影响较大,p+1是β的维数,n是样本容量。
dffits(model, infl = , res = )
COVRATIO准则
若有一个样本点所对应的COVRATIO值离1越远,则认为该样本点影响越大。
covratio(model, infl = lm.influence(model, do.coef = FALSE),
res = weighted.residuals(model))
影响分析的概括函数 influen.mesures(model)
每种方法找到的点是否是真正的强影响点,还需要根据具体情况进行分析。该函数返回一个列表,包括DFFITS统计量,COVRATIO统计量,Cook距离等。
例:电影院老板调查电视广告的费用X1和报纸广告的费用X2对每周总收入Y的影响(单位:元)试给出回归分析,并进行回归诊断。
X1 X2 Y X1 X2 Y 1500 5000 96000 2000 2000 90000 1500 4000 95000 2500 2500 92000 3300 3000 95000 2300 3500 95000 4200 2500 94000 2500 3000 94000
> x1<-c(1500,1500,3300,4200,2000,2500,2300,2500)
> x2<-c(5000,4000,3000,2500,2000,2500,3500,3000)
> y<-c(96000,95000,95000,94000,90000,92000,95000,94000)
> money<-data.frame(x1,x2,y)
> lm.reg<-lm(y~x1+x2,money)
> summary(lm.reg)
Call:
lm(formula = y ~ x1 + x2, data = money)
Residuals:
1 2 3 4 5 6 7 8
-845 492 492 -508 -483 -301 622 531
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.32e+04 1.71e+03 48.55 7e-08 ***
x1 1.30e+00 3.49e-01 3.72 0.01374 *
x2 2.34e+00 3.31e-01 7.06 0.00088 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 700 on 5 degrees of freedom
Multiple R-squared: 0.909, Adjusted R-squared: 0.872
F-statistic: 24.9 on 2 and 5 DF, p-value: 0.00251
> influence.measures(lm.reg)
Influence measures of
lm(formula = y ~ x1 + x2, data = money) :
dfb.1_ dfb.x1 dfb.x2 dffit cov.r cook.d hat inf
1 1.98495 0.06107 -3.8115 -5.167 0.0461 2.2838 0.633 *
2 0.11517 -0.26496 0.1105 0.533 1.7687 0.1018 0.301
3 -0.19968 0.33167 0.1285 0.468 1.7188 0.0791 0.262
4 0.88978 -1.56524 -0.3538 -1.871 1.8860 1.0056 0.660 *
5 -1.53634 1.11782 1.4109 -1.633 2.1558 0.8133 0.645 *
6 -0.16907 0.08580 0.1621 -0.242 2.1804 0.0233 0.226
7 -0.00772 -0.00518 0.1016 0.383 1.2356 0.0499 0.140
8 0.10067 -0.03095 -0.0686 0.305 1.4686 0.0335 0.132
可以看出第1、4、5个观测点为强影响点。第1个样本点的cook.d=2.2838>>4/8=0.5;第4个样本点的cov.r=1.8860与1距离很远;第5个样本点的|dffit|=1.633>>2√2/8=1,故这三个点被认为是强影响点。
8.4.3 共线性诊断
共线性问题是指拟合多元线性回归时,自变量之间存在线性关系或近似线性关系。这将会隐蔽变量的显著性,增加参数估计的误差,还会产生一个不稳定的模型。因此,共线性诊断就是找出哪些变量之间存在共线关系,主要有以下几种方法:
特征值法
把X‘X变换为主对角线是1的矩阵,然后求特征值和特征向量。若有r个特征值近似等于0,则回归设计阵X中有r个共线性关系,且共线性关系的系数向量就是近似为0的特征值对应的特征向量。
计算矩阵特征值和特征向量的函数:
eigen(x, symmetric, only.values = FALSE, EISPACK = FALSE)
x是所求矩阵;symmetric规定矩阵的对称性;only.values = FALSE表示返回特征值和特征向量,否则只返回特征值。
条件指数
若自变量的交叉乘积矩阵X’X的特征值为d21≥d22≥…≥d2k,则X的条件数d1/dk就是刻画矩阵的奇异性的一个指标,故称d1/dj ( j=1,…,k)为条件指数。
一般认为条件指数在10~ 30为弱相关;30 ~100为中等相关;大于100表明有强相关性。
kappa(z, exact = FALSE, norm = NULL, method = c("qr", "direct"), ...)
z是矩阵;exact = FALSE近似计算条件数,否则精确计算条件数。
方差膨胀因子VIF
是指回归系数的估计量由于自变量共线性使得方差增加的一个相对度。
对第j个回归系数,它的膨胀因子为:
VIFj = 第j个回归系数的方差/自变量不相关时第j个回归系数的方差
= 1/(1-R2j) = 1/TOLj
其中1-R2j是自变量xj对模型中其余自变量线性回归模型的R平方,TOLj 也称容限(Tolerence)。
一般VIF>10,表明模型中有很强的共线性问题。
vif(obj, digits=5)
例:某种水泥在凝固时单位质量所释放的热量为Y卡/千克,它与水泥中的四种化学成分有关。试对自变量的共线性进行诊断。
X1 X2 X3 X4 Y 7 26 6 60 78.5 1 29 15 52 74.3 11 56 8 20 104.3 11 31 8 47 87.6 7 52 6 33 95.9 11 55 9 22 109.2 3 71 17 6 102.7 1 31 22 44 72.5 2 54 18 22 93.1 21 47 4 18 115.9 1 40 23 34 83.8 11 66 9 12 113.3 10 68 8 12 109.4
> x1<-c(7,1,11,11,7,11,3,1,2,21,1,11,10)
> x2<-c(26,29,56,31,52,55,71,31,54,47,40,66,68)
> x3<-c(6,15,8,8,6,9,17,22,18,4,23,9,8)
> x4<-c(60,52,20,57,33,22,6,44,22,18,34,12,12)
> y<-c(78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3,109.4)
> cement<-data.frame(x1,x2,x3,x4,y)
> lm.reg<-lm(y~x1+x2+x3+x4,cement)
> summary(lm.reg)
Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = cement)
Residuals:
Min 1Q Median 3Q Max
-3.278 -1.396 -0.237 1.165 4.038
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 64.804 22.887 2.83 0.0221 *
x1 1.480 0.360 4.12 0.0034 **
x2 0.492 0.229 2.15 0.0635 .
x3 0.051 0.330 0.15 0.8810
x4 -0.156 0.212 -0.74 0.4820
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.37 on 8 degrees of freedom
Multiple R-squared: 0.983, Adjusted R-squared: 0.975
F-statistic: 119 on 4 and 8 DF, p-value: 3.74e-07
> library(DAAG)
> vif(lm.reg,digits=3)
x1 x2 x3 x4
9.544 26.936 9.513 31.357
> cor(x2,x4)
[1] -0.948
X2 与 X4 的VIF>10,且线性相关系数接近0.95,因此可以肯定他们之间存在严重的共线性。
8.5 Logistic回归
线性回归分析要求响应变量Y是连续型变量。在研究两元分类响应变量与诸多自变量之间的相互关系时,常选用logistic回归模型。
Logistic回归
将两元分类响应变量Y的一个结果记为“成功”,另一个结果记为“失败”,分别用1和0表示。对响应变量Y有影响的p个自变量(解释变量)记为X1, X2,…, Xp,在p个自变量的作用下出现成功的条件概率记为p=P(Y=1|X1, X2,…,Xp)
logit(p)=ln(p/(1-p))=β0+β1X1+β2X2+…+βpXp
logistic回归模型(略),对其作logit变换可将其写成上述线性形式,进而使用线性回归模型对参数β进行估计。
广义线性模型
logistic回归模型属于广义线性模型的一种,是通常的正态线性模型的推广,要求响应变量只能通过线性形式依赖于解释变量。
1)基于正态分布的广义线性模型:(默认)
glm(formula, family = gaussian(link = identity), data=data.frame)
formula是拟合公式;family是分布族;link指定使用的连接函数;data数据框;
2)基于二项分布的广义线性模型:
glm(formula, family = binominal(link = logit), data=data.frame)
公式formula有两种输入方法,一种像线性模型通常数据的输入法,另一种是输入成功与失败的次数。
3)基于泊松分布的广义线性模型:
glm(formula, family = poisson(link = log), data=data.frame)
4)基于伽马分布的广义线性模型:
glm(formula, family = gamma(link = inverse), data=data.frame)
例:下表为对45名驾驶员的调查结果,其中X1表示视力状况(是一个分类变量,1表示好,0表示有问题);X2表示年龄;X3表示驾车教育(是一个分类变量,1表示参加过驾车教育,0表示没有);Y是分类型输出变量(1表示去年出过事故,0表示去年没有出过事故),试考察前三个变量与发生事故的关系。
X1 X2 X3 Y X1 X2 X3 Y X1 X2 X3 Y 1 17 1 1 1 68 1 0 0 17 0 0 1 44 0 0 1 18 1 0 0 45 0 1 1 48 1 0 1 68 0 0 0 44 0 1 1 55 0 0 1 48 1 1 0 67 0 0 1 75 1 1 1 17 0 0 0 55 0 1 0 35 0 1 1 70 1 1 1 61 1 0 0 42 1 1 1 72 1 0 1 19 1 0 0 57 0 0 1 35 0 1 1 69 0 0 0 28 0 1 1 19 1 0 1 23 1 1 0 20 0 1 1 62 1 0 1 19 0 0 0 38 1 0 0 39 1 1 1 72 1 1 0 45 0 1 0 40 1 1 1 74 1 0 0 47 1 1 0 55 0 0 1 31 0 1 0 52 0 0 0 68 0 1 1 16 1 0 0 55 0 1 0 25 1 0 1 61 1 0
> #输入数据
> x1<-rep(c(1,0,1,0,1),c(5,10,10,10,10))
> x2<-c(17,44,48,55,75,35,42,57,28,20,38,45,47,52,55,68,18,68,48,17,70,72,35,19,62,39,40,55,68,25,17,45,44,67,55,61,19,69,23,19,72,74,31,16,61)
> x3<-c(1,0,1,0,1,0,1,0,0,0,1,0,1,0,0,1,1,0,1,0,1,1,0,1,1,1,1,0,0,1,0,0,0,0,0,1,1,0,1,0,1,1,0,1,1)
> y<-c(1,0,0,0,1,1,1,0,1,1,0,1,1,0,1,0,0,0,1,0,1,0,1,0,0,1,1,0,1,0,0,1,1,0,1,0,0,0,1,0,1,0,1,0,0)
> accident<-data.frame(x1,x2,x3,y)
>
> #作logistic回归
> log.glm<-glm(y~x1+x2+x3,family = binomial,data = accident)
> summary(log.glm)
Call:
glm(formula = y ~ x1 + x2 + x3, family = binomial, data = accident)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.564 -0.913 -0.789 0.964 1.600
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.5976 0.8948 0.67 0.504
x1 -1.4961 0.7049 -2.12 0.034 *
x2 -0.0016 0.0168 -0.10 0.924
x3 0.3159 0.7011 0.45 0.652
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 62.183 on 44 degrees of freedom
Residual deviance: 57.026 on 41 degrees of freedom
AIC: 65.03
Number of Fisher Scoring iterations: 4
> #模型诊断与更新:由于参数β2,β3没有通过检验,故用step()做变量筛选
> log.step<-step(log.glm)
Start: AIC=65.03
y ~ x1 + x2 + x3
Df Deviance AIC
- x2 1 57.0 63.0
- x3 1 57.2 63.2
<none> 57.0 65.0
- x1 1 61.9 67.9
Step: AIC=63.03
y ~ x1 + x3
Df Deviance AIC
- x3 1 57.2 61.2
<none> 57.0 63.0
- x1 1 62.0 66.0
Step: AIC=61.24
y ~ x1
Df Deviance AIC
<none> 57.2 61.2
- x1 1 62.2 64.2
> summary(log.step)
Call:
glm(formula = y ~ x1, family = binomial, data = accident)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.449 -0.878 -0.878 0.928 1.510
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.619 0.469 1.32 0.187
x1 -1.373 0.635 -2.16 0.031 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 62.183 on 44 degrees of freedom
Residual deviance: 57.241 on 43 degrees of freedom
AIC: 61.24
Number of Fisher Scoring iterations: 4
> #预测分析
> log.pre<-predict(log.step,data.frame(x1=1))
> p1<-exp(log.pre)/(1+exp(log.pre));p1
1
0.32
> log.pre<-predict(log.step,data.frame(x1=0))
> p2<-exp(log.pre)/(1+exp(log.pre));p2
1
0.65
说明视力有问题的司机发生交通事故的概率是视力正常的司机的两倍以上


