计算机系统结构 第一章：概述

计算机系统结构 第一章：概述

星川之下皆萤火尘埃
我独行在人潮你天真而待
相遇若是借丹青着色
青原上 绯樱如海
——银临《青原樱》

本章知识结构图：

概述

历史

Flynn分类法

计算机体系结构

发展趋势

性能测试

计算机设计的量化原理

一、历史

世界上第一台通用电子计算机“埃尼阿克”于1946年诞生于美国宾夕法尼亚大学。

计算机性能的发展源于

• 半导体技术的发展。
• 计算机体系结构的发展。

计算机技术发展的历史：

• 1978-1986 处理器性能的增长主要是半导体技术驱动。
• 1986-2003 虽然半导体技术发展迅速，但是这一阶段的飞速发展更归功于体系结构和组织思想的发展。（超过50%的年增长率）
• 2004至今 硬件复兴结束。
  原因：功耗，ILP开发受限。
  发展方向：数据级并行（DLP），线程级并行（TLP）。

二、Flynn分类法

• 单指令流、单数据流，SISD。
• 单指令流、多数据流，SIMD。
• 多指令流、单数据流，MISD。
• 多指令流、多数据流，MIMD。

①SISD

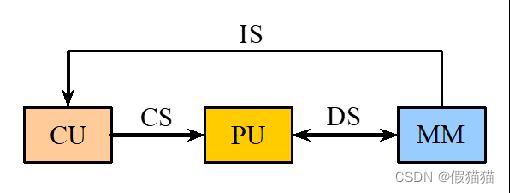
这个类别是单处理器；
可以使用指令级并行，如流水线、动态调度、超标量。

②SIMD

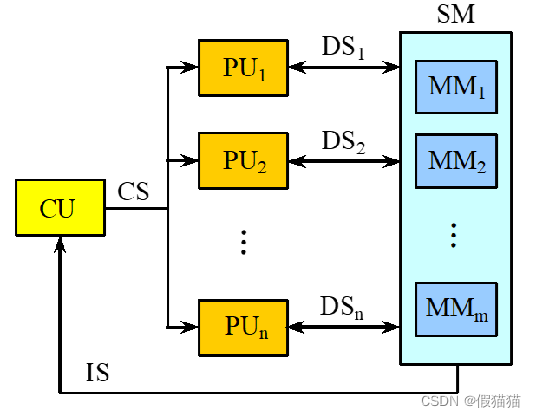
同一指令操纵多条数据流，由不同处理器，对多个数据项进行并行数据处理；
每个数据处理器可有自己的数据存储器，但是只有一个指令存储器和控制器；
例：向量体系结构，GPU。

③MIMD

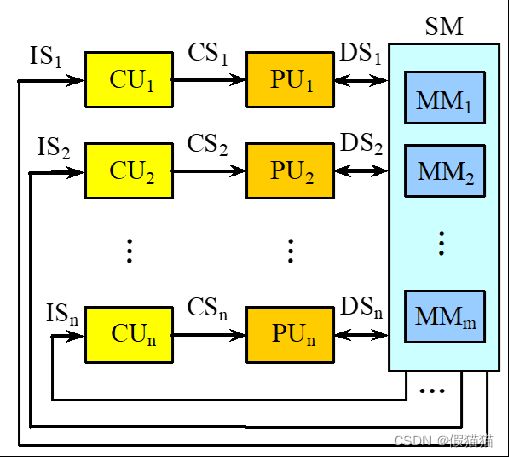
每个处理器都自己取指令，并对自己的数据进行处理；
任务级并行；
紧密耦合的MIMD结构—线程级并行；
松散耦合MIMD结构—集群。

④ MISD

目前为止，没有此种类型的商用机；
脉动阵列。

MISD个人理解就类似于多路选择器。

三、计算机体系结构

计算机体系结构的定义

狭义的定义（Amdahl的定义）：

• 指令集的设计；
• 需要考虑：寄存器、内存地址、访存方式、指令集的设计；
• 经典定义：机器语言程序员所见到的计算机的属性，即概念性结构和功能特性。

广义的定义 （《计算机体系结构-量化研究方法》中的定义）：

包括计算机设计所有三个方面：

• 指令集结构
• 组成
• 硬件

指令集结构（ISA）：区分软件和硬件的界限

分类：

现在几乎所有的ISA都划分为通用寄存器体系结构中；

两种主流版本：

• 寄存器-存储器，如80X86；
• 载入-存储，如ARM和MIPS。

存储器寻址：

• 字节寻址：几乎所有
• 访问对齐：一个大小为s的对象，其字节地址为A；如果A mod s=0，则访问对齐。ARM和MIPS操作对象必须对齐

寻址模式：

• 立即寻址
• 寄存器寻址
• 偏移寻址

操作数类型和大小

指令类型：

• 数据传输
• 算逻运算
• 控制指令
• 浮点指令

指令格式：

• 固定
• 可变

组成和硬件

• 组成是计算机的逻辑实现，包括存储系统、存储器连接、CPU内部设计。
• 硬件是计算机的具体实现，包括详尽的逻辑设计和封装技术。

四、发展趋势

①技术趋势

不可或缺的实现技术

不可或缺的实现技术

集成电路技术

DRAM

闪存

磁盘技术

网络技术

性能趋势：带宽与延迟

带宽（吞吐量）：

• 单位时间的工作量
• 处理器的带宽增长 32,000-40,000 倍
• 内存和磁盘的带宽增长 300-1200 倍

延迟（响应时间）：

• 一个事件从开始到完成所经历的时间
• 处理器响应时间改进 50-90 倍
• 内存和磁盘的响应时间改进 6-8 倍

显然，在这些技术的发展过程中，带宽的改进要明显优于延迟。一个简单的经验法则是：带宽的增长速度至少是延迟改进速度的平方。

晶体管（Transistors）性能与连线（wire）的发展

集成电路的制造工艺是以特征尺寸来衡量的

• 特征尺寸 就是一个晶体管或者一条连线在x方向或者y方向的最小尺寸。
• 特征尺寸：1971为 10 微米， 2011年0.032微米（32纳米技术），2017年 0 .016微米（16纳米技术）。
• 特征尺寸下降时，晶体管性能以线性提升。
  随着特征尺寸缩小，连线会变短，但是单位长度的电阻和电容都会变差。和晶体管性能相比，连线延迟方面的改进少的可怜。
• 晶体管的密度将以平方曲线上升。

②功率和能耗趋势

功率和能耗：系统观点

• 处理器需要的最大功率，对确保正确操作非常重要。
• 持续功耗 – 热设计功耗 （Thermal Design Power， TDP）
  决定了冷却需求；
  当温度接近节点温度上限时，电路降低时钟频率，从而减小功率；如果不成功，启动热过载启动装置，以降低芯片的功率。
• 能耗和能耗效率。

微处理器内部的能耗和功率

• 动态能耗
• 时钟频率和电源电压保持不变的情况下，提高能耗效率。
  关闭非活动模块，以节省能耗和动态功率；
  动态电压-频率调整。微处理器可以提供不同工作频率。
  针对典型情景的设计，PMD、笔记本等的省电模式；
  超频。Intel在2008年开始提供Turbo模式，在这种模式下，芯片可以判定在少数几个核心上以较高的时钟频率短时间运行。

③成本趋势

• 时间、产量和大众化影响
• 集成电路成本
• 成本与价格
• 制造成本与运行成本

五、性能测试

1. 性能指标
   响应时间/执行时间 – 用户关心的
   吞吐量 – 仓库级计算机的操作人员关心的

2. 加速比
   机器X比机器Y快， 是什么意思？ – 执行时间是稳定、可靠的性能度量

3. 执行时间
   墙上时间: 包括所有的系统开销
   CPU时间: only computation time

4. 基准测试
   程序内核 ：实际应用程序中的短小、关键部分；
   玩具程序：为了完成编程入门作业而编写的小程序，通常不超过100行，如快排程序；
   合成基准测试程序：为了匹配实际应用程序的特征和行为编写的虚拟程序；
   基准测试套件：衡量处理器处理各种应用程序的性能。优势在于任何一个基准测试的弱点都会因为其他基准测试的存在而变小。最常用的是SPEC。

六、计算机设计的量化原理

充分利用并行

并行性的含义：计算机系统在同一时刻或者同一时间间隔内进行多种运算或操作。即只要在时间上相互重叠，就存在并行性。

• 同时性：两个或两个以上的事件在同一时刻发生。
• 并发性：两个或两个以上的事件在同一时间间内发生。

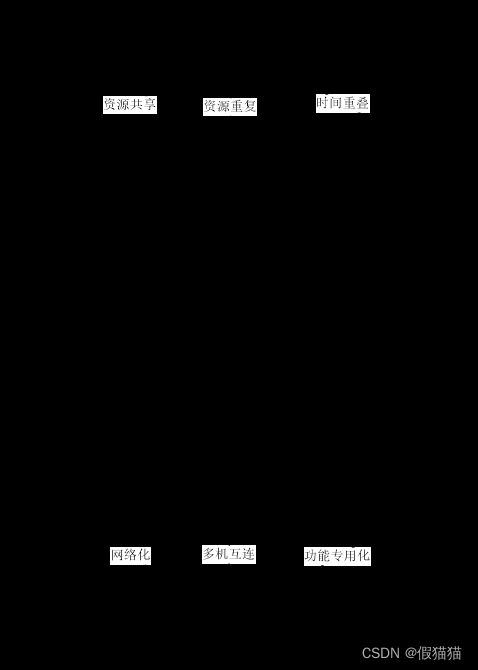
提高并行性的三种途径：

• 时间重叠： 引入时间因素，让多个处理过程在时间上相互错开，轮流重叠地使用同一套硬件设备的各个部分，以加快硬件周转而赢得速度。
• 资源重复：引入空间因素，以数量取胜。通过重复设置硬件资源，大幅度地提高计算机系统的性能。
• 资源共享：这是一种软件方法，它使多个任务按一定时间顺序轮流使用同一套硬件设备。如，多道程序。

时间重叠

单处理机中 – 部件功能专用化（流水线）

• 把一件工作按功能分割为若干相互联系的部分；
• 把每一部分指定给专门的部件完成；
• 按时间重叠原理把各部分的执行过程在时间上重叠起来，使所有部件依次分工完成一组同样的工作。

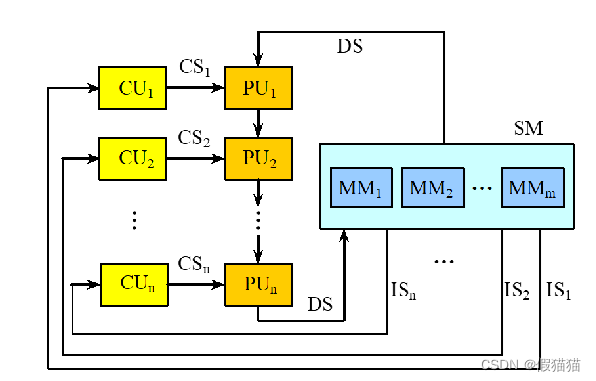
多处理机中 – 处理机专用化

• 专用外围处理机： 例如，输入/输出功能的分离。
• 专用处理机：如数组运算、高级语言翻译、数据库管理等，分离出来。
• 异构型多处理机系统：由多个不同类型、至少担负不同功能的处理机组成，它们按照作业要求的顺序，利用时间重叠原理，依次对它们的多个任务进行加工，各自完成规定的功能动作。

资源重复

单处理机中 – 重复设置功能部件

• 多存储体并行
• 数据/指令独立存储体
• 重复设置运算部件

多处理机中 – 重复设置处理机

• 容错系统
• 同构型多处理机系统：由多个同类型或至少担负同等功能的处理机组成，它们同时处理同一作业中能并行执行的多个任务。

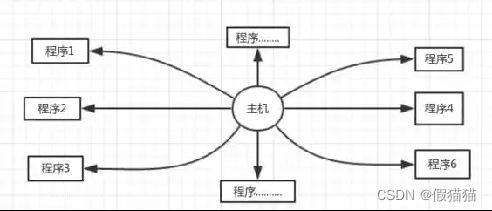
资源共享

单处理机中：分时系统

多处理机中：分布式系统

单机系统和多机系统中并行性的发展

局部性原理

程序执行时所访问的存储器地址分布不是随机的，而是相对地簇聚。

• 常用的一个经验规则：程序执行时间的90%都是在执行程序中10%的代码。
• 程序的时间局部性：程序即将用到的信息很可能就是目前正在使用的信息。
• 程序的空间局部性：程序即将用到的信息很可能与目前正在使用的信息在空间上相邻或者临近。

重点关注常见情形

• 对经常发生的情况采用优化方法的原则进行选择，以得到更多的总体上的改进。
• 优化是指分配更多的资源、达到更高的性能或者分配更多的电能等。
• 例如：
  相对溢出，不溢出是经常性事件。针对不溢出的情况进行性能设计，无需花过多的时间和精力在解决溢出上。
  处理器的取值、译码比乘法器用的更加频繁，优先优化取指令和译码部件。

Amdahl定律

加速比 – 衡量系统的性能改进了多少（通常>1）

$$加速比=\frac{系统功{能}_{改进后}}{系统功{能}_{改进前}}=\frac{\frac{1}{总执行时{间}_{改进后}}}{\frac{1}{总执行时{间}_{改进前}}}=\frac{总执行时{间}_{改进前}}{总执行时{间}_{改进后}}$$

换个方式来看，

$$\begin{array}{rl}总执行时{间}_{改进后}& =不可改进部分的执行时间+可改进部分改进后执行时间\\ & =(1-可改进比例)\times 总执行时{间}_{改进前}+\frac{可改进比例\times 总执行时{间}_{执行前}}{部件加速比}\\ & =总执行时{间}_{改进前}\times [(1-可改进比例)+\frac{可改进比例}{部件加速比}]\end{array}$$

因此，
$$加速比=\frac{1}{(1-可改进比例)+\frac{可改进比例}{部件加速比}}$$

• 可改进比例：在改进前的系统中，可改进部分的执行时间在总的执行时间中所占的比例。
  例如：一个需运行60秒的程序中有20秒的运算可以加速，那么这个比例就是20/60。
• 部件加速比：可改进部分改进以后，性能提高的倍数。它是改进前所需的执行时间与改进后执行时间的比。 一般情况下部件加速比是大于1的。
  例如：若系统改进后，可改进部分的执行时间是2秒，而改进前其执行时间为5秒，则部件加速比为5/2。

Amdahl定律表明：加快某部件执行速度所能获得的系统性能加速比，受限于该部件的执行时间占系统中总执行时间的百分比。

Amdahl定律：一种性能改进的递减规则

• 如果仅仅对计算任务中的一部分做性能改进，则改进得越多，所得到的总体性能的提升就越有限。
• 重要推论：如果只针对整个任务的一部分进行改进和优化，那么所获得的加速比不超过1/(1-可改进比例)。

公式拓展：假设S_i为第i种部件的加速比，P_i为第i种部件执行时间占总执行时间中的比例。

则
$$加速比=\frac{1}{(1-可改进比例)+\frac{可改进比例}{部件加速比}}=\frac{1}{(1-\sum P_i)+\sum \frac{P_i}{S_i}}$$

CPU性能公式

执行一个程序所需的CPU时间：
$$CPU时间=IC\times CPI\times 时钟周期时间$$

IC为指令条数，CPI为每条指令执行的平均时钟周期数。
其中，IC由编译技术和指令集结构决定，CPI由指令集结构和计算机组成决定，时钟周期时间由计算机组成和硬件实现技术决定。
在指令集结构中，CISC→RISC：IC上升，CPI下降。

CPI时间公式拓展
假设：计算机系统有n种指令，
$$\begin{array}{c}CP{I}_i：第i种指令的处理时间（周期数）\\ I{C}_i：在程序中第i种指令出现的次数\end{array}$$
则
$$\begin{array}{rl}CPU时间& =执行指令所需的时钟周期数\times 时钟周期时间\\ & =\sum _{i=1}^n(CP{I}_i\times I{C}_i)\times 时钟周期时间\end{array}$$
$$CPI=\frac{时钟周期数}{IC}=\frac{{\sum }_{i=1}^n(CP{I}_i\times I{C}_i)}{IC}=\sum _{i=1}^n(CP{I}_i\times \frac{I{C}_i}{IC})$$

$$其中，\frac{I{C}_i}{IC}反映了第i种指令在程序中所占的比例。$$

摩尔定律

单芯片上可容纳的晶体管数目，约每隔18个月便会增加一倍，性能也将提升一倍。

Dennard定律

晶体管面积的缩小使得其所消耗的电压以及电流会以差不多相同的比例缩小。也就是说，如果晶体管的大小减半，该晶体管的静态功耗将会降至四分之一（电压电流同时减半）。

练习题

填空题

1.世界第一台通用电子计算机诞生于（）年。
2.计算机性能的发展源于（）的发展和（）的发展。
3.区分硬件和软件的界限的是（）。
4.特征尺寸下降后，晶体管性能以（）提升；晶体管密度将以（）提升。

1.1946
2.半导体技术 计算机体系结构
3.指令集结构（ISA）
4.线性 平方曲线

问答题

1.硬件复兴结束的原因和新的发展方向？

原因：功耗，ILP开发受限。
发展方向：数据级并行（DLP），线程级并行（TLP）。

2.Flynn分类法，具体举例？

SISD，如流水线，动态调度，超标量。
SIMD，如向量体系结构，GPU。
MIMD，如线程级并行，集群。
MISD，如脉动阵列。

3.计算机体系结构的定义？

狭义的定义：机器语言程序员所见到的计算机的属性，即概念性结构和功能特性。
广义的定义：包括计算机设计的所有三个方面：指令集结构，组成，硬件。

4.并行性的含义？

计算机系统在同一时刻或者同一时间间隔内进行多种运算或操作。即只要在时间上相互重叠，就存在并行性。

• 同时性：两个或两个以上的事件在同一时刻发生。
• 并发性：两个或两个以上的事件在同一时间间隔内发生。

5.提高并行性的三种途径。

• 时间重叠： 引入时间因素，让多个处理过程在时间上相互错开，轮流重叠地使用同一套硬件设备的各个部分，以加快硬件周转而赢得速度。
• 资源重复：引入空间因素，以数量取胜。通过重复设置硬件资源，大幅度地提高计算机系统的性能。
• 资源共享：这是一种软件方法，它使多个任务按一定时间顺序轮流使用同一套硬件设备

6.以下部件属于哪种方式提高并行性？
（1）流水线（2）专用处理机（3）异构型多处理机（4）同构型多处理机
（5）分时系统（6）分布式系统（7）虚拟存储器（8）并行处理机

时间重叠：（1）（2）（3）
资源重复：（4）（8）
资源共享：（5）（6）（7）

7.量化原理中“重点关注常见情形”概念，举例。

对经常发生的情况采用优化方法的原则进行选择，以得到更多的总体上的改进。优化是指分配更多的资源、达到更高的性能或者分配更多的电能等。
例如：相对溢出，不溢出是经常性事件。针对不溢出的情况进行性能设计，无需花过多的时间和精力在解决溢出上；处理器的取值、译码比乘法器用的更加频繁，优先优化取指令和译码部件。

8.简述摩尔定律的内容。

单芯片上可容纳的晶体管数目，约每隔18个月便会增加一倍，性能也将提升一倍。

9.简述Dennard定律的内容。

晶体管面积的缩小使得其所消耗的电压以及电流会以差不多相同的比例缩小。也就是说，如果晶体管的大小减半，该晶体管的静态功耗将会降至四分之一（电压电流同时减半）。

计算题

1. 将计算机系统中某一功能的处理速度提高到原来的20倍，但该功能的处理时间仅占整个系统运行时间的40%，则采用此提高性能的方法后，能使整个系统的性能提高多少？

衡量系统的性能改进了多少使用加速比。
$$加速比=\frac{1}{(1-可改进比例)+\frac{可改进比例}{部件加速比}}=\frac{1}{(1-40\%)+\frac{40\%}{20}}=1.613$$

2. 考虑条件分支指令的两种不同设计方法：
   （1）CPUA：通过比较指令设置条件码，然后测试条件码进行分支。
   （2）CPUB：在分支指令中包括比较过程。
   在这两种CPU中，条件分支指令都占用2个时钟周期，而所有其他指令占用1个时钟周期。对于CPUA，执行的指令中分支指令占20%；由于每条分支指令之前都需要有比较指令，因此比较指令也占20%。由于CPUA在分支时不需要比较，因此CPUB的时钟周期时间是CPUA的1.1倍。问：哪一个CPU更快？

$$CP{I}_A=2\times 20\%+1\times 80\%=1.2$$
$$CPU时{间}_A=IC\times CP{I}_A\times 时钟周期时{间}_A=1.2IC\times 时钟周期时{间}_A$$
由于CPUB不包含比较指令，因此CPUB指令数的CPUA的80%，且CPUB中分支指令所占比例为20%/(1-20%)=25%.
$$CP{I}_B=2\times 25\%+1\times 75\%=1.25$$
$$\begin{array}{rl}CPU时{间}_B& =I{C}_B\times CP{I}_B\times 时钟周期时{间}_B\\ & =(IC\times 0.8)\times 1.25\times (1.1\times 时钟周期时{间}_A)\\ & =1.1IC\times 时钟周期时{间}_A\end{array}$$
综上所述，CPUB更快。

3. 图形处理器中经常需要的一种转换是求平方根。浮点（FP）平方根的实现在性能方面有很大差异，特别是在为图形设计的处理器中尤为明显。假设FP平方根（FPSQR）占用一项关键图形基准测试中20%的执行时间。有一项提议：升级FPSQR硬件，使这一运算速度提高到原来的10倍。另一项提议是让图形处理器中所有FP指令的运行速度提高到原来的1.6倍，FP指令占用该应用程序一半的执行时间。设计团队相信，他们使所有FP指令执行速度提高到1.6倍所需要的工作量与加快平方根运算的工作量相同。试比较这两种设计方案。

①升级FPSQR硬件
$$加速{比}_1=\frac{1}{(1-20\%)\times \frac{20\%}{10}}=1.22$$
②所有FP指令速度提高1.6倍
$$加速{比}_2=\frac{1}{(1-50\%)\times \frac{50\%}{1.6}}=1.23$$
第二种方案稍好一些。

4. 假设已经进行如下测量：

• FP操作频率=25%
• FP操作的平均CPI=4.0
• 其他指令的平均CPI=1.33
• FPSQR的频率=2%
• FPSQR的CPI=20

假定有两种设计方案，一种方案将FPSQR的CPI降至2，一种是把所有FP操作的平均CPI降至2.5。请对比这两种设计方案。

需要注意的是，FPSQR操作是在FP操作之中的，他们的CPI不是相互独立的。因此，求方案1的CPI不能直接使用性能公式，而是要从原CPI的基础上减去改进的部分。方案2则使用性能公式或者减去改进的部分均可。
$$\begin{array}{c}未改进前：CP{I}_0=25\%\times 4+75\%\times 1.33=1.9975\\ 方案1：CP{I}_1=CP{I}_0-2\%\times (CP{I}_{旧FPSQR}-CP{I}_{新FPSQR})\\ =1.9975-2\%\times (20-2)=1.6375\\ 方案2：CP{I}_2=CP{I}_0-25\%\times (CP{I}_{旧FP}-CP{I}_{新FP})\\ =1.9975-25\%\times (4-2.5)=1.6225\end{array}$$
$$加速{比}_1=\frac{IC\times CP{I}_0\times 时钟周期时间}{IC\times CP{I}_1\times 时钟周期时间}=\frac{CP{I}_0}{CP{I}_1}=1.22$$
$$加速{比}_2=\frac{IC\times CP{I}_0\times 时钟周期时间}{IC\times CP{I}_2\times 时钟周期时间}=\frac{CP{I}_0}{CP{I}_2}=1.23$$
方案2稍好一些。

5. 某台主频为400MHz的计算机执行标准测试程序，程序中指令类型、执行数量和平均时钟周期数如下：

指令类型	指令执行数量	平均时钟周期数
整数	45000	1
数据传送	75000	2
浮点	8000	4
分支	1500	2

求该计算机的有效CPI和程序执行时间。

MHz单位与之对应。
$$CPI=\frac{45000\times 1+75000\times 2+8000\times 4+1500\times 2}{129500}=1.776$$
$$程序执行时间=IC\times CPI\times \frac{1}{时钟频率}=129500\times 1.776\times \frac{1}{400}=575s$$

6. 计算机系统中有三个部件可以改进，这三个部件的部件加速比为：
   部件加速比1=30； 部件加速比2=20； 部件加速比3=10
   （1）如果部件1和部件2的可改进比例均为30%，那么当部件3的可改进比例为多少时，系统加速比才可以达到10？
   （2）如果三个部件的可改进比例分别为30%、30%和20%，三个部件同时改进，那么系统中不可加速部分的执行时间在总执行时间中占的比例是多少？

(1)
$$系统加速比=\frac{1}{(1-可改进比{例}_1-可改进比{例}_2-可改进比{例}_3)+\frac{可改进比{例}_1}{部件加速比1}+\frac{可改进比{例}_2}{部件加速{比}_2}+\frac{可改进比{例}_3}{部件加速{比}_3}}=10$$
设部件3的可改进比例为x，得方程
$$\frac{1}{(0.4-x)+0.01+0.015+0.1x}=10$$
解得x=36.1%,即部件3的可改进比例为36.1%.
(2)
设改进前的总执行时间为T，则不可加速部分的执行时间为0.3T.
$$系统加速比=\frac{1}{(1-30\%-30\%-20\%)+\frac{30\%}{30}+\frac{30\%}{20}+\frac{20\%}{10}}=4.08$$
$$总执行时{间}_{改进后}=\frac{T}{4.08}=0.245T$$
因此
$$系统中不可加速部分的执行时间在总执行时间中占的比例=\frac{0.2T}{0.245T}=81.6\%$$

7. 假设某应用程序中有4类操作，通过改进，各操作获得不同的性能提高。具体数据如下表所示：

操作类型	程序中的数量（百万条指令）	改进前的执行时间（周期）	改进后的执行时间（周期）
操作1	10	2	1
操作2	30	20	15
操作3	35	10	3
操作4	15	4	1

（1）改进后，各类操作的加速比分别是多少？
（2）4类操作均改进后，整个程序的加速比是多少？

(1)
$$\begin{array}{rl}部件加速{比}_1=\frac{2}{1}& =1\\ 部件加速{比}_2=\frac{20}{15}& =1.33\\ 部件加速{比}_3=\frac{10}{3}& =3.33\\ 部件加速{比}_4=\frac{4}{1}& =4\end{array}$$
(2)
注意有多个误区：

• 表格中程序的数量为“百万条指令”，误以为指令总数为100万条，从而便于计算指令所占比例。其实从题干“假设某应用程序中有4类操作”可知程序一共就只有这4种操作，总数90万条，不及100万。
• 正常会想到用Amdahl定律的部件加速比去做，但是可改进比例是可改进部分所占时间的比例，而不是指令条数所占的比例。
• 因此，使用表格原始数据计算前后的执行时间的比即可，这也是加速比公式的原始形式。
  $$加速比=\frac{总执行时{间}_{改进前}}{总执行时{间}_{改进后}}=\frac{10\times 20+30\times 20+35\times 10+15\times 4}{\times 1+30\times 15+35\times 3+15\times 1}=1.78$$