python代码讲解-PCA主成分分析 原理讲解 python代码实现
1. 用途:
通俗来说: 考察一个人的智力情况,就直接看数学成绩就行(存在:数学、语文、英语成绩) 。就是找出一个最主要的特征,然后进行分析。
数据压缩 (Data Compression) ,将高维数据变为低维数据。
可视化数据 (3D->2D等)
2. 2D-->1D,nD-->kD
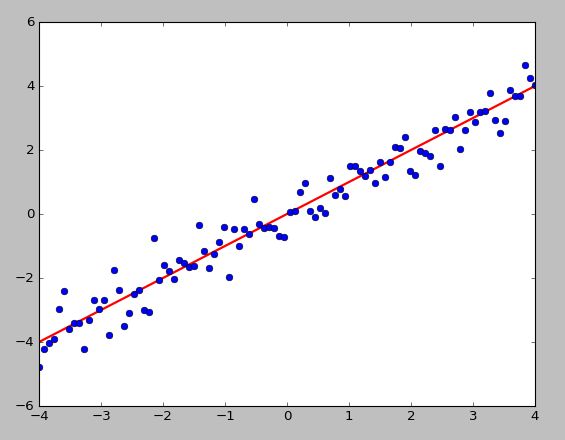
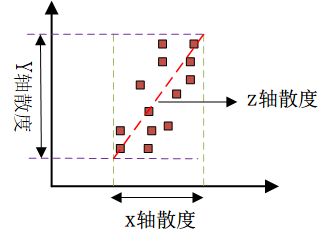
如下图所示,所有数据点可以投影到一条直线,是投影距离的平方和(投影误差)最小
注意数据需要归一化处理
思路是找1个向量u,所有数据投影到上面使投影距离最小
那么nD-->kD就是找k个向量,所有数据投影到上面使投影误差最小
eg:3D-->2D,2个向量就代表一个平面了,所有点投影到这个平面的投影误差最小即可
3. 降维原理(数学推导)
# 归一化数据
def featureNormalize(X):
'''(每一个数据-当前列的均值)/当前列的标准差'''
n = X.shape[1]
mu = np.zeros((1,n));
sigma = np.zeros((1,n))
mu = np.mean(X,axis=0)
sigma = np.std(X,axis=0)
for i in range(n):
X[:,i] = (X[:,i]-mu[i])/sigma[i]
return X,mu,sigma
Sigma = np.dot(np.transpose(X_norm),X_norm)/m # 求Sigma
(3)求?的特征值和特征向量。
eigVals,eigVects = np.linalg.eig(np.mat(Sigma))
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0]) # index,1 = 1; index,2 = 2; index,0 = 3
>>> y = np.argsort(x)
>>> y[::-1]
array([0, 2, 1])
>>> y[:-3:-1]
array([0, 2]) # 取出 -1, -2
>>> y[:-6:-1]
array([0, 2, 1])
eigValInd = argsort(eigVals)
# print 'eigValInd1=', eigValInd
# -1表示倒序,返回topN的特征值[-1 到 -(topNfeat+1) 但是不包括-(topNfeat+1)本身的倒叙]
eigValInd = eigValInd[:-(topNfeat+1):-1]
# print 'eigValInd2=', eigValInd
# 重组 eigVects 最大到最小
redEigVects = eigVects[:, eigValInd]
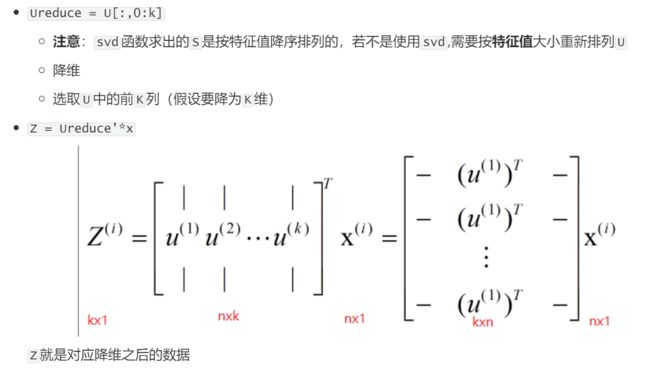
(5)求降维后的数值
lowDDataMat = meanRemoved * redEigVects