特征值和特征向量概述-面试必问3(含特征值、向量意义)

特征值和特征向量（Eigenvalues and eigenvectors）

在线性代数中，一个线性变换的特征向量（eigenvector 或者 characteristic vector）是一个非零向量。将线性变换应用在它上面，它最多以一个标量因子进行伸缩变换。特征向量缩放的因子叫做特征值，记为 $\lambda$ 。

几何上，一个特征向量，对应于一个实非零特征值，指向它被变换拉伸的方向，特征值是它被拉伸的因子。如果特征值是负的，则方向相反，如果特征值为0，则缩回原点。

不严谨地说，在多维向量空间中，特征向量是不会旋转的。

正式定义

如果 $T$ 一个线性变换，是一个从在 数域 $F$ 上的向量空间 $V$ 到它自身的映射。$\mathbf{v}$ 是一个在 $V$ 内的非零向量。则 $\mathbf{v}$ 是一个 $T$ 的特征向量如果 $T(\mathbf{v})$ 是 $\mathbf{v}$ 的数乘（scalar multiple）。形式化地，
$$T(\mathbf{v})=\lambda \mathbf{v},$$
其中， $\lambda$ 是一个 $F$ 内的标量，即特征值（eigenvalue或者characteristic value）。

由于存在 $n\times n$ 的方阵 和 从 $n$ 维向量空间到自身的线性变换之间直接的一一对应关系，而且是给定向量空间中的任意基的情况下。因此，在一个有限维的向量空间内，用矩阵的语言或者是线性变换的语言来定义特征值和特征向量是等价的。

如果 $V$ 是有限维的，上述等式与
$$A\mathbf{u}=\lambda \mathbf{u}$$
等价。其中 $A$ 是 $T$ 的矩阵表示，$\mathbf{u}$ 是 $\mathbf{v}$ 的坐标向量（用坐标来表示的向量）。

概述（Overview）

特征值和特征向量在线性变换分析中占有突出地位。前缀 eigen- 取自德语单词 eigen（与英语单词 own 同源），表示“正确”、“特征”、“拥有”。特征值和特征向量最初用于研究刚体旋转运动的主轴，具有广泛的应用，例如稳定性分析、振动分析、原子轨道、面部识别和矩阵对角化。

此处的蒙娜丽莎示例提供了一个简单的说明。图像上的每个点都可以表示为从图像中心指向该点的向量。本例中的线性变换称为 shear 映射。上半部分的点向右移动，下半部分的点向左移动。指向原始图像中每个点的向量因此向右或向左倾斜，并通过变换变长或变短。应用此变换时，沿水平轴的点根本不会移动。因此，任何直接指向右侧或左侧且没有垂直分量的向量都是此变换的特征向量，因为映射不会改变其方向。此外，这些特征向量都有一个等于 1 的特征值，因为映射也不会改变它们的长度。

在这个 shear 映射中，红色箭头改变方向，但蓝色箭头没有。蓝色箭头是此 shear 映射的特征向量，因为它不改变方向，并且由于其长度不变，因此其特征值为 1。

线性变换可以采用多种不同的形式，将向量映射到多种向量空间中，因此特征向量也可以采用多种形式。例如，线性变换可以是一个微分算子（differential operator），如 $\frac{\mathrm{d}}{\mathrm{d}x}$。在这种情况下，特征向量是的函数，被称为特征函数（本征函数，eigenfunctions），特征向量是被微分算子scaled的，比如
$$\frac{\mathrm{d}}{\mathrm{d}x}{e}^{\lambda x}=\lambda e^{\lambda x}$$
或者，线性变换可以采用 $n\times n$ 矩阵的形式，在这种情况下，特征向量是 $n\times 1$ 矩阵。如果线性变换以 $n\times n$ 矩阵 $A$ 的形式表示，则上述线性变换的特征值方程可以重写为矩阵乘法
$$A\mathbf{v}=\lambda \mathbf{v}$$
其中特征向量 $\mathbf{v}$ 是一个 $n\times 1$ 矩阵。对于矩阵，特征值和特征向量可用于分解矩阵——例如通过对其进行对角化。

特征值和特征向量产生了许多密切相关的数学概念，并且在命名它们时可以随意使用前缀 eigen-：

• 线性变换的所有特征向量的集合，每个特征向量都与其对应的特征值配对，称为该变换的特征系统（eigensystem）。
• 对应于相同特征值的 $T$ 的所有特征向量的集合，加上零向量，称为特征空间（eigenspace），或被称为与该特征值相关的 $T$ 的特征空间。
• 如果 $T$ 的一组特征向量形成 $T$ 的domain基，则该基称为特征基（eigenbasis）。

历史

特征值通常在线性代数或矩阵理论的背景下被引入。然而，从历史上看，它们出现在二次型和微分方程（quadratic forms and differential equations）的研究中。

18 世纪，Leonhard Euler 研究了刚体的旋转运动，发现了主轴的重要性。Joseph-Louis Lagrange 意识到主轴是惯性矩阵的特征向量。（惯性张量的特征值和特征向量分别是主惯性矩和主惯性轴的方向）

在 19 世纪初，Augustin-Louis Cauchy 看到了他们的工作如何用于对二次曲面（quadric surfaces）进行分类，并将其推广到任意维度。柯西还创造了术语 racine caractéristique（特征根），即现在所谓的特征值；他的术语存在于特征方程中。

后来，约瑟夫·傅立叶在他 1822 年的著名著作《Théorie analytique de la chaleur》中，利用拉格朗日和皮埃尔-西蒙·拉普拉斯的工作，通过变量分离来求解热方程。Charles-François Sturm 进一步发展了傅立叶的思想，并引起了柯西的注意，柯西将它们与自己的思想结合起来，得出了实对称矩阵（real symmetric matrices）具有实特征值的事实。 1855 年，Charles Hermite 将其扩展为现在称为 Hermitian 矩阵。

大约在同一时间，Francesco Brioschi 证明了正交矩阵的特征值位于单位圆（unit circle）上，和 Alfred Clebsch 发现了反对称矩阵（斜对称矩阵，skew-symmetric matrices）的相应结果。最后，Karl Weierstrass 通过意识到亏损矩阵会导致不稳定，阐明了拉普拉斯提出的稳定性理论中的一个重要方面。

与此同时，Joseph Liouville 研究了类似于 Sturm 的特征值问题；从他们的工作中产生的学科现在被称为 Sturm-Liouville 理论。施瓦茨在 19 世纪末研究了拉普拉斯方程在一般域上的第一个特征值，而庞加莱在几年后研究了泊松方程。

20 世纪初，大卫希尔伯特通过将算子视为无限矩阵来研究积分算子的特征值。他是第一个使用德语单词 eigen 的人，意思是“拥有”，表示 特征值和特征向量，在1904年。尽管他可能一直在遵循赫尔曼·冯·亥姆霍兹的相关用法。一段时间以来，英语中的标准术语是“proper value”，但更独特的术语“eigenvalue”是今天的标准。

第一个计算特征值和特征向量的数值算法出现在 1929 年，当时 Richard von Mises 发表了power method。当今最流行的方法之一，QR 算法，由 John G. F. Francis 和 Vera Kublanovskaya 于 1961 年独立提出。

矩阵特征值和特征向量

特征值和特征向量通常在以矩阵为重点的线性代数课程中介绍给我们。此外，有限维向量空间上的线性变换可以使用矩阵来表示，这在数值和计算应用中尤其常见。

矩阵 A 通过拉伸向量 x 而不改变其方向来起作用，因此 x 是 A 的特征向量

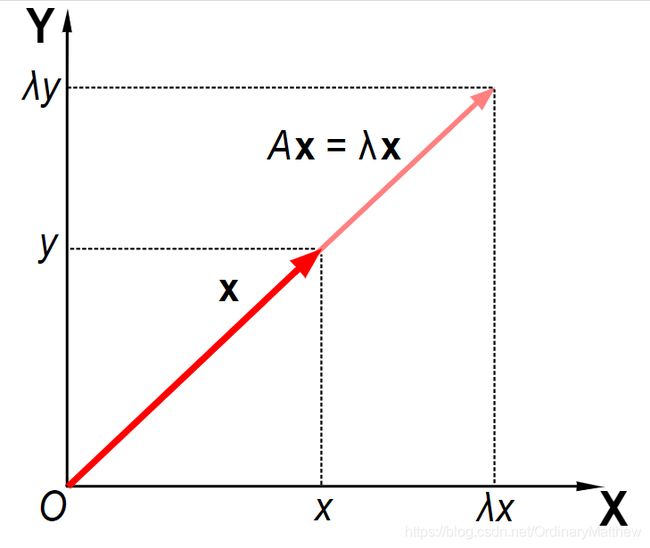
考虑形成为 n 个标量列表的 n 维向量，例如三维向量
$$\mathbf{x}=\left[\begin{array}{c}1\\ -3\\ 4\end{array}\right]\mathbf{y}=\left[\begin{array}{c}-20\\ 60\\ -80\end{array}\right]$$
$\mathbf{x}\mathbf{y}$ 是相互的 标量倍数（scalar multiples），或平行或共线（parallel or collinear），如果有一个标量 $\lambda$ 使得
$$\mathbf{x}=\lambda \mathbf{y}$$
在上面的例子中，$\lambda =-\frac{1}{20}$.

现在考虑由 $n\times n$ 矩阵 $A$ 定义的 $n$ 维向量的线性变换，
$$A\mathbf{v}=\mathbf{w}$$
或者
$$\left[\begin{array}{ccc}{A}_{11}& A_{12}& \cdots A_{1n}\\ A_{21}& A_{22}& \cdots A_{2n}\\ ⋮& ⋮& ⋮\\ A_{n1}& A_{n2}& \cdots A_{nn}\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_n\end{array}\right]$$
对于每一行
$$w_i=A_{i1}{v}_1+A_{i2}{v}_2+\cdots +A_{in}{v}_n=\sum _{j=1}^n{A}_{ij}{v}_j$$
如果 存在 $\mathbf{v}$ 和 $\mathbf{w}$ 是标量倍数关系，即如果
$$A\mathbf{v}=\mathbf{w}=\lambda \mathbf{v}\text{\hspace{1em}(1)}$$
则 $\mathbf{v}$ 是线性变换 $A$ 的一个特征向量，标量因子 $\lambda$ 是特征值，对应于那个特征向量。方程（$1$） 是矩阵 $A$ 特征值方程。

方程（$1$）可以等价地写成
$$(A-\lambda I)\mathbf{v}=0\text{\hspace{1em}(2)}$$
其中 $I$ 是 $n$ 阶单位矩阵。

特征值和特征多项式（characteristic polynomial）

方程（ $2$）有一个非零解 $v$ 当且仅当 矩阵 $A-\lambda I$ 的行列式是 $0$ 。所以 $A$ 的特征值是满足下面方程的 $\lambda$
$$|A-\lambda I|=0\text{\hspace{1em}(3)}$$
根据 行列式的定义（Leibniz’s rule），方程( $3$ ) 是一个关于变量 $\lambda$ 的多项式函数，多项式的阶数是 $n$ （矩阵 $A$ ）的阶数。多项式的系数取决于 $A$ ，除了 $n$ 阶的项总是 $(-1{)}^n{\lambda }^n$ 。这个多项式被称作 $A$ 的特征多项式。 方程( $3$ ) 被称作 $A$ 的特征方程（the characteristic equation or the secular equation）。

代数学基本定理（The fundamental theorem of algebra）指出 $n\times n$ 矩阵的特征多项式，作为一个 $n$ 阶多项式，可以被分解为 $n$ 个线性项的乘积：
$$|A-\lambda I|=({\lambda }_1-\lambda )({\lambda }_2-\lambda )\dots ({\lambda }_n-\lambda ),\text{\hspace{1em}(4)}$$
其中，${\lambda }_i$ 是复数域上的数。${\lambda }_1,{\lambda }_2,\dots {\lambda }_n$ 是多项式的根和矩阵 $A$ 的特征值，不一定拥有不同的值。

作为一个简短的例子，在后面的例子部分更详细地描述，考虑矩阵
$$A=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$$
取$(A-\lambda I)$的行列式，$A$的特征多项式为
$$|A-\lambda I|=\left[\begin{array}{cc}2-\lambda & 1\\ 1& 2-\lambda \end{array}\right]=3-4\lambda +{\lambda }^2$$
令特征多项式为零，它的根为 $\lambda =1$ 和 $\lambda =3$，这是 $A$ 的两个特征值。每个特征值对应的特征向量可以通过求解方程 $\left(A-\lambda I\right)\mathbf{v}=0$得到。在这个例子中，特征向量是
$${\mathbf{v}}_{\lambda =1}=\left[\begin{array}{c}1\\ -1\end{array}\right],{\mathbf{v}}_{\lambda =3}=\left[\begin{array}{c}1\\ 1\end{array}\right]$$
的任何数乘向量。

如果矩阵 A 的元素都是实数，那么特征多项式的系数也将是实数，但特征值可能仍然有非零虚部（nonzero imaginary parts）。因此，相应特征向量的元素也可能具有非零虚部。类似地，即使 $A$ 的所有元素都是有理数，或者即使它们都是整数，特征值也可能是无理数。

具有实系数的实多项式的非实根可以分组为复共轭对，即每对复共轭的两个成员具有仅符号不同的虚部和相同的实部。如果阶数是奇数，则根据intermediate value 定理，根中至少有一个是实数。因此，任何奇数阶实矩阵至少有一个实特征值，而偶数阶实矩阵可能没有任何实特征值。与复数特征值相关联的特征向量也是复数并且也出现在复共轭对中。

代数重数（Algebraic multiplicity）

令 ${\lambda }_i$ 为 $n\times n$ 矩阵 $A$ 的一个特征值。特征值的代数重数 ${\mu }_A({\lambda }_i)$ 是其作为特征多项式根的多重性，即最大整数 $k$ 使得 $(\lambda -\lambda i{)}^k$ 整除该多项式。

假设矩阵 $A$ 具有维度 $n$ ，且 $d\le n$ 个不同的特征值。而等式 $(4)$ 将 $A$ 的特征多项式分解为 $n$ 个线性项的乘积，其中一些项可能重复，而特征多项式可以写为 d 项的乘积，每个项对应于一个不同的特征值，每个项的指数是代数重数，
$$|A-\lambda I|=({\lambda }_1-\lambda {)}^{u_A({\lambda }_1)}({\lambda }_1-\lambda {)}^{u_A({\lambda }_2)}\dots ({\lambda }_1-\lambda {)}^{u_A({\lambda }_d)}$$
如果 $d=n$ 那么 右式是 $n$ 个线性项，上式就和等式（$4$）一样了。每个特征值的代数重数大小和 维度 $n$ 有下列关系
$$\begin{gathered} 1\le u_A({\lambda }_i)\le n \\ {u}_A=\sum _{i=1}^d{u}_A({\lambda }_i)=n \end{gathered}$$
如果 $u_A({\lambda }_i)=1$ ，那么 ${\lambda }_i$ 被称作一个simple特征值。 如果 $u_A({\lambda }_i)$ 和 ${\lambda }_i$ 的几何重数（在下一section介绍）相等，那么 ${\lambda }_i$ 被称作 semisimple 特征值。

特征空间，几何重数，和矩阵的特征基（Eigenspaces，geometric multiplicity，and the eigenbasis for matrices）

给定 $n\times n$ 矩阵 $A$ 的特定特征值 $\lambda$，将集合 $E$ 定义为满足方程 ($2$) 的所有向量 $\mathbf{v}$，
$$E=\{\mathbf{v}:(A-\lambda I)\mathbf{v}=0\}$$
一方面，这个集合是矩阵 $(A-\lambda I)$的核或零空间。另一方面，根据定义，任何满足此条件的非零向量都是与 $\lambda$ 关联的 $A$ 的特征向量。因此，集合 $E$ 是零向量与与 $\lambda$ 关联的 $A$ 的所有特征向量的集合的并集，并且 集合$E$ 等于 $(A-\lambda I)$ 的零空间。$E$ 称为与 $\lambda$ 相关的 $A$ 的特征空间（eigenspace ，characteristic space）。一般来说，$\lambda$ 是一个复数，特征向量是复数 $n\times 1$ 矩阵。零空间的一个性质是它是一个线性子空间，所以 $E$ 是 ${\mathbb{C}}^n$ 的一个线性子空间。

因为特征空间 $E$ 是一个线性子空间，所以它在加法下是封闭的。也就是说，如果两个向量 $\mathbf{u}$ 和 $\mathbf{v}$ 属于集合 $E$，记作 $\mathbf{u},\mathbf{v}\in E$，则 $\mathbf{u}+\mathbf{v}\in E$ 或等效地 $A(u+v)=\lambda (u+v)$。这可以使用矩阵乘法的分配特性(distributive property)来验证。类似地，因为 $E$ 是一个线性子空间，它在标量乘法下是封闭的。也就是说，如果 $\mathbf{v}\in E$ 并且 $\alpha$ 是一个复数，则 $(\alpha \mathbf{v})\in E$ 或等效地 $A(\alpha \mathbf{v})=\lambda (\alpha \mathbf{v})$。这可以通过注意到复数矩阵乘以复数是可交换的来检查。只要 $\mathbf{u}+\mathbf{v}$ 和 $\alpha \mathbf{v}$ 不为零，它们也是与 $\lambda$ 关联的 $A$ 的特征向量。

与 $\lambda$ 相关联的特征空间 $E$ 的维数，或等效地与 $\lambda$ 相关联的线性无关特征向量的最大数量，被称为特征值的几何重数 $\gamma A(\lambda )$。因为 $E$ 也是 $(A-\lambda I)$的零空间，$\lambda$ 的几何重数是 $(A-\lambda I)$ 的零空间的维度，也称为 $(A-\lambda I)$ 的零空间
$$\gamma A(\lambda )=n-rank(A-\lambda I)$$

注：不同的特征向量可以对应同一个特征值，或者说同一个特征值可以对应多个特征向量。因为特征向量是和矩阵对应的，一个矩阵表示一个线性变换。特征向量就是在这次线性变换中只伸缩，不旋转的向量。特征值就是这次线性变换作用在这个特征向量上时，这个特征向量的伸缩倍数。所以多个不同的特征向量是可以伸缩同样的倍数的，即可以有相同的特征值。

特征值的其他性质

$令A是一个任意的n\times n复数矩阵，其特征值为{\lambda }_1,\dots ,{\lambda }_n。$每个特征值在这个列表中出现 ${\mu }_A({\lambda }_i)$ 次，其中 ${\mu }_A({\lambda }_i)$ 是特征值的代数重数。以下是该矩阵及其特征值的属性：

• $A$ 的迹，定义为其对角线元素之和，也是所有特征值之和
  $$tr(A)=\sum _{i=1}^n{a}_{ii}=\sum _{i=1}^n{\lambda }_1+{\lambda }_2+\cdots +{\lambda }_n$$

• A 的行列式是其所有特征值的乘积，
  $$|A|=\prod _{i=1}^n{\lambda }_i$$

• 矩阵 $A$ 的 $k$ （k为正整数）次幂$A^k$ 的特征值为 ${\lambda }_1^k,\dots ,{\lambda }_n^k$ 。

• 矩阵 $A$ 可逆当且仅当 它的每个特征值都非零。

• 如果 $A$ 是可逆的，那么 $A^{-1}$ 的特征值为 $\frac{1}{{\lambda }_1},\dots ,\frac{1}{{\lambda }_n}$， 并且每个特征值的几何重数对应相等。此外，由于逆的特征多项式是原多项式的reciprocal polynomial，特征值共享相同的代数重数。

• 如果 $A$ 等于它的共轭转置 $A^{\ast }$，或者等价地，如果 $A$ 是 Hermitian，那么每个特征值都是实数。这同样适用于任何对称实矩阵。

• 如果 $A$ 不仅是 Hermitian，而且还是正定、正半定、负定或负半定，则每个矩阵的特征值分别为正、非负、负或非正。

• 如果$A$ 是幺正（unitary）的，每个特征值都有绝对值 $|{\lambda }_i|=1$。

• 如果 $A$ 是一个 $n\times n$ 矩阵和 $\{{\lambda }_1,\dots ,{\lambda }_k\}$ 是它的特征值，那么矩阵 $I+A$ 的特征值（其中 $I$ 是单位矩阵）是 $\{{\lambda }_1+1,\dots ,{\lambda }_k+1\}$。此外，如果 $\alpha \in \mathbb{C}$， $\alpha I+A$ 的特征值是$\{{\lambda }_1+\alpha ,\dots ,{\lambda }_k+\alpha \}$。更一般地，对于多项式 $P$，矩阵 $P(A)$ 的特征值是 $\{P({\lambda }_1),\dots ,P({\lambda }_k)\}$。

左右特征向量

许多学科传统上将向量表示为具有单列的矩阵，而不是具有单行的矩阵。因此，矩阵上下文中的“特征向量”一词几乎总是指右特征向量，即右乘 $n\times n$ 矩阵 $A$ 的列向量定义方程，方程（$1$）
$$A\mathbf{v}=\lambda \mathbf{v}$$
特征值和特征向量问题也可以定义为左乘矩阵$A $的行向量。在这个公式中，定义方程是:
$$\mathbf{u}A=\kappa \mathbf{u}$$
其中 $\kappa$ 是一个标量，而且 $\mathbf{u}$ 是一个 $1\times n$ 的矩阵。任何满足上述方程的 行向量 $\mathbf{u}$ 被称作 矩阵 $A$ 的左特征向量， $\kappa$ 被称作与左特征向量相关的特征值。对上述方程取转置，得：
$$A^T{\mathbf{u}}^T=\kappa {\mathbf{u}}^T$$
将此等式与等式 ($1$) 进行比较，可以立即得出 $A$ 的左特征向量与 $A^{\text{T}}$具有相同的特征值。此外，由于 $ A^{\textsf {T}}$ 的特征多项式与 $A$ 的特征多项式相同，所以$A$ 的左特征向量的特征值与 $A^{\text{T}}$ 的右特征向量的特征值相同。

对角化和特征分解（Diagonalization and the eigendecomposition）

假设 $A$ 的特征向量形成一个基，或者等价地，$A$ 有 $n$ 个线性无关的特征向量 $v_1,v_2,...,v_{1n}$ 以及相关的特征值 ${\lambda }_1,{\lambda }_2,...,{\lambda }_n$。特征值不需要是不同的。定义一个方阵 $Q$，其列是 $A$ 的 $n$ 个线性无关的特征向量，
$$Q=[{\mathbf{v}}_1,{\mathbf{v}}_2\dots {\mathbf{v}}_n]$$
由于 $Q$ 的每一列都是 $A$ 的特征向量，因此将 $A$ 乘以 $Q$ 将 $Q$的每一列按其关联的特征值缩放，
$$AQ=[{\lambda }_1{\mathbf{v}}_1{\lambda }_2{\mathbf{v}}_2\dots {\lambda }_{\mathbf{n}}{\mathbf{v}}_{\mathbf{n}}]$$
考虑到这一点，定义一个对角矩阵 $\Lambda$，其中每个对角元素 ${\Lambda }_{ij}$ 是与 $Q$ 的第 $i$ 列相关联的特征值。然后
$$AQ=Q\Lambda$$
因为 $Q$ 的列是线性无关的，所以 $Q$ 是可逆的。等式两边右乘 $Q^{-1}$
$$A=Q\Lambda Q^{-1}$$
或者等式两边左乘 $Q^{-1}$ ，得
$$Q^{-1}AQ=\Lambda$$
因此，$A$ 可以分解为由其特征向量组成的矩阵、特征值沿对角线的对角矩阵以及特征向量矩阵的逆矩阵。这称为特征分解(eigendecomposition)，它是一种相似变换。这样的矩阵 $A$ 被称为相似于对角矩阵 $\Lambda$ 或可对角化的。矩阵 $Q$ 是相似变换的基矩阵的变更（change of basis matrix of the similarity transformation）。本质上，矩阵 $A$ 和 $\Lambda$代表以两个不同基表示的相同线性变换。当将线性变换表示为 $\Lambda$ 时，特征向量用作基。

相反，假设矩阵 $A$ 是可对角化的。设 $P$ 是一个非奇异方阵，使得 $P^{-1}AP$ 是某个对角矩阵 $D$。左乘 $P$，$AP=PD$。因此，$P$ 的每一列必须是 $A$ 的特征向量，其特征值是 $D$ 的对应对角元素。由于 $P$ 的列必须线性无关才能使 $P$ 可逆，因此 $A$ 存在 $n$ 个线性无关的特征向量。进而，$A$ 的特征向量形成一个基当且仅当 A 是可对角化的。

不可对角化的矩阵称为亏损的(defective)。对于有亏损的矩阵，特征向量的概念推广到广义特征向量，特征值的对角矩阵推广到 Jordan 范式。在代数闭域上，任何矩阵 A 都具有 Jordan 范式，因此允许广义特征向量的基和分解为广义特征空间。

惯性张量

采用直角坐标系的三个坐标轴为参考轴，一个刚体的惯性张量 $\mathcal{I}$，以矩阵形式表达为
$$\left[\begin{array}{ccc}{I}_{xx}& I_{xy}& I_{xz}\\ I_{yx}& I_{yy}& I_{yz}\\ I_{zx}& I_{zy}& I_{zz}\end{array}\right]$$
其中，矩阵的元素以方程表达为
$$\begin{gathered} I_{xx}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\int y^2+z^{2}dm{I}_{xy}=I_{yx}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}-\int xydm \\ {I}_{yy}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\int x^2+z^{2}dm{I}_{xz}=I_{zx}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}-\int xzdm \\ {I}_{zz}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\int x^2+y^{2}dm{I}_{yz}=I_{zy}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}-\int yzdm \end{gathered}$$
$(x,y,z)$是刚体内部的微小体积元 $dm$的位置。惯性张量 $\mathcal{I}$是个实值三阶对称矩阵，对角元素 $I_{xx},I_{yy},I_{zz}$ 分别为刚体对于 x-轴， y-轴，z-轴的转动惯量。非对角元素 $I_{\alpha \beta }，\alpha \ne \beta$ 是刚体对于 $\alpha$-轴和 $\beta$-轴的惯量积。根据谱定理，可以使惯性张量成为一个对角矩阵。所得到的三个特征值必定是正实值；三个特征向量必定正交。

换另外一种方法，我们需要求解特征方程
$$\mathcal{I}\mathbf{\omega }=\lambda \mathbf{\omega }$$
也就是以下行列式等于零的三次方程：
$$\left|\begin{array}{ccc}{I}_{xx}-\lambda & I_{xy}& I_{xz}\\ I_{yx}& I_{yy}-\lambda & I_{yz}\\ \mathcal{I}\mathbf{\omega }=\lambda {\mathbf{\omega }}_{zx}& I_{zy}& I_{zz}-\lambda \end{array}\right|=0$$
这方程的三个根 ${\lambda }_1{\lambda }_2{\lambda }_3$ 都是正实的特征值。将特征值带入特征方程，再加上方向余弦（directional cosine）方程，${\omega }_x^2+{\omega }_y^2+{\omega }_z^2=1$。就可以求到特征向量
$${\hat{\mathbf{\omega }}}_1{\hat{\mathbf{\omega }}}_2{\hat{\mathbf{\omega }}}_3$$
。这些特征向量都是刚体的惯量主轴；而这些特征值则分别是刚体对于惯量主轴的主转动惯量。

其他

1. 特征值和特征向量在PCA中的应用请移步PAC、SVD以及它们的联系之充分数学知识推导
2. 因子分析、图的特征值、特征脸、应力张量薛定谔方程、分子轨域、振动分析中特征值和特征向量的应用请移步参考文献1或者2。

参考文献

1. Eigenvalue and Eigenvector from wiki
2. 特征值和特征向量 来自维基百科
3. 两个特征值相等则特征向量是否相等？来自知乎