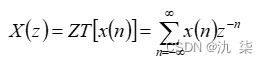数字信号处理三：离散时间LTI系统的z域分析

一、z变换

序列x(n)的z变换定义为

其中，符号ZT表示取z变换，z是复变量。
如果信号的z域表示式X(z)是有理函数，进行逆z变换的一个方法是对X(z)进行部分分式展开，然后求各简单分式的逆z变换。设X(z)的有理分式表示为

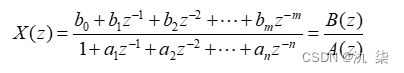
（注意：此处分子和分母多项式均按z的负幂次排列，第一项为常数项。）
scipy库中提供了一个对 进行部分分式展开的函数signal.residuez，语句格式为

r,p,k = signal.residuez(b,a)

b，a分别表示X(z)的分子与分母多项式的系数向量；
r为部分分式的系数向量；
p为极点向量；
k为多项式的系数。若X(z)为有理真分式，则k为零。

【例1】已知 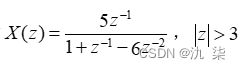求逆z变换。

程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal

b=[0,5]
a=[1,1,-6]
r,p,k = signal.residuez(b,a)
print('分子系数',r)
print('极点',p)
print('多项式系数',k)

程序运行结果为：
分子系数 [ 1. -1.]
极点 [ 2. -3.]
多项式系数 []

从运行结果可知，有两个极点：P1=2,P2=-3,所以，X(z)的部分分式展开为：

因此，其逆z变换为:

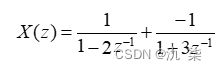
【例2】已知 求逆z变换。

程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal

b=[0,-3]
a=[2,-5,2]
r,p,k = signal.residuez(b,a)
print('分子系数',r)
print('极点',p)
print('多项式系数',k)

程序运行结果为：
分子系数 [ 1. -1.]
极点 [0.5 2. ]
多项式系数 []

从运行结果可知，有两个极点：P1=0.5,P2=2,所以，X(z)的部分分式展开为：

因此，其逆z变换为

【例3】 已知 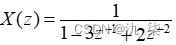，若序列x(n)为因果序列，求x(n)，并写出X(z)的收敛域。

程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal

b=[1]
a=[1,-3,2]
r,p,k = signal.residuez(b,a)
print('分子系数',r)
print('极点',p)
print('多项式系数',k)

显示结果：
分子系数 [-1. 2.]
极点 [1. 2.]
多项式系数 []

从运行结果可知，有两个极点：p1=1，p2=2,所以，X(z)的部分分式展开为：

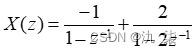
因此，其逆z变换为

X(z)的收敛域为：|z|>2

二、系统函数的零极点分析

LTI离散时间系统的系统函数定义为系统零状态响应的z变换与激励的z变换之比，即

如果系统函数H(z)的有理函数表示式为

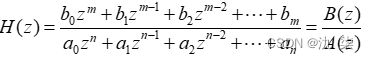
（注意：此处分子和分母多项式均按z的正幂次排列，最后一项为常数项。）
则系统函数的零极点可通过scipy库中的函数signal.tf2zpk得到，语句格式为

z, p, k = signal.tf2zpk(b, a)

z为零点，p为极点，k为增益系数，
b和a分别表示H(z)的分子与分母多项式的系数向量。

此函数的作用是将H(z)的有理分式表达式转换为零极点增益形式，即

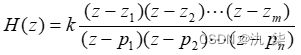
【例4】 已知一离散因果LTI系统的系统函数为 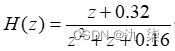求该系统的零点和极点。

程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal

b=[1,0.32]
a=[1,1,0.16]
z,p,k=signal.tf2zpk(b, a)
print('零点是',z)
print('极点是',p)
print('增益系数为',k)

程序运行结果显示为：
零点是 [-0.32]
极点是 [-0.8 -0.2]
增益系数为 1.0

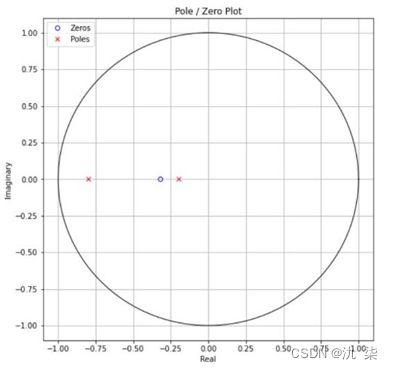
因此，零点为z=-0.32，极点为 p1=-0.8与 p2=-0.2。
若要获得系统函数 的零极点分布图，可利用绘图函数plt.plot把零点和极点画出来。程序代码示例如下：

plt.figure(figsize=(6,6))
plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
plt.plot(np.real(p), np.imag(p), 'xr')
plt.legend(['Zeros', 'Poles'],loc=2)
plt.title('Pole / Zero Plot')
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.grid()
plt.show()

程序运行结果如下图所示：

一般我们在绘制零极点分布图时，都会画出单位圆，以便更清楚的表示零点和极点与单位圆的位置关系，所以在上述代码的基础上，我们增加绘制单位圆的代码如下：

th=np.linspace(0,2*np.pi,300)
x=np.cos(th)
y=np.sin(th)
plt.plot(x,y,"-k",linewidth=1)

程序运行结果如下图所示：

【例5】 已知一离散因果LTI系统的系统函数为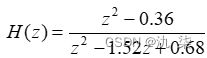绘出该系统的零极点分布图。

程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal

b=[1,0,-0.36]
a=[1,-1.52,0.68]
z,p,k=signal.tf2zpk(b,a)
print('零点是',z)
print('极点是',p)
print('增益系数为',k)
plt.figure(figsize=(6,6))
plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
plt.plot(np.real(p), np.imag(p), 'xr')
plt.legend(['Zeros', 'Poles'],loc=2)
plt.title('Pole / Zero Plot')
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.grid()

th=np.linspace(0,2*np.pi,300)
x=np.cos(th)
y=np.sin(th)
plt.plot(x,y,"-k",linewidth=1)
plt.show()

程序运行结果如下：
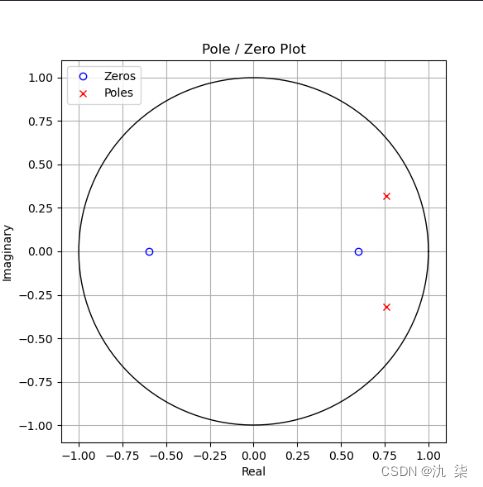
零点是 [ 0.6 -0.6]
极点是 [0.76+0.32j 0.76-0.32j]
增益系数为 1.0
零极点分布图如下图所示。可见，该因果系统的极点全部在单位圆内，故系统是稳定的。

三、系统函数的零极点分布与其时域特性的关系

在离散系统中，z变换建立了时域函数和h(n)与z域函数H(z)之间的对应关系。因此，系统函数H(z)可以反映时域信号 的部分内在性质。
若要求得系统的单位脉冲响应h(n)，可用scipy库中的函数signal.dimpulse实现，其语句格式为：

t,y=signal.dimpulse(s,n=N)

n代表计算单位脉冲响应的样值个数，通常为正整数；
参数s代表系统，可用scipy库中的函数signal.dlti实现，语句格式为：

s=signal.dlti(b,a)
b与a分别表示H(z)的分子和分母多项式的系数向量。

我们仍旧通过讨论H(z)的极点情况，来说明系统函数的零极点分布与系统时域特性的关系。

【例6】 画出下列系统函数的零极点分布图、以及对应的时域单位脉冲响应 的波形，并分析系统函数的极点对时域波形的影响。

（1）
（2）

第（1）小题程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
from matplotlib.font_manager import FontProperties

font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
b=[1,0]
a=[1,-0.8]
z,p,k=signal.tf2zpk(b,a)
print('零点是',z)
print('极点是',p)
print('增益系数为',k)
plt.figure(figsize=(12,6))
plt.subplot(121)
plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
plt.plot(np.real(p), np.imag(p), 'xr')
plt.legend(['Zeros', 'Poles'],loc=2)

plt.title('极点是在单位圆内的正实数',fontproperties=font_set)
plt.xlabel('实部',fontproperties=font_set)
plt.ylabel('虚部',fontproperties=font_set)
plt.grid('on')

th=np.linspace(0,2*np.pi,300)
x=np.cos(th)
y=np.sin(th)
plt.plot(x,y,"-k",linewidth=1)
s=signal.dlti(b,a)
t,y=signal.dimpulse(s,n=30)

plt.subplot(122)
plt.stem(t, np.squeeze(y))
plt.title('单位脉冲响应h(n)',fontproperties=font_set)
plt.xlabel('n')
plt.ylabel('h(n)')
plt.grid('on')
plt.show()

程序运行结果如下图所示：

第（2）小题程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
from matplotlib.font_manager import FontProperties

font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
b=[1,0]
a=[1,0.8]
z,p,k=signal.tf2zpk(b,a)
print('零点是',z)
print('极点是',p)
print('增益系数为',k)
plt.figure(figsize=(12,6))
plt.subplot(121)
plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
plt.plot(np.real(p), np.imag(p), 'xr')
plt.legend(['Zeros', 'Poles'],loc=2)

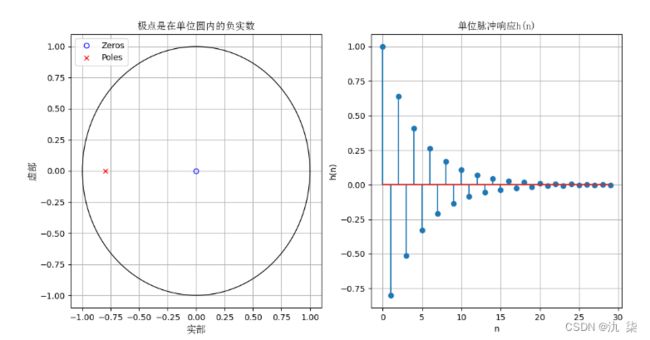
plt.title('极点是在单位圆内的负实数',fontproperties=font_set)
plt.xlabel('实部',fontproperties=font_set)
plt.ylabel('虚部',fontproperties=font_set)
plt.grid('on')

th=np.linspace(0,2*np.pi,300)
x=np.cos(th)
y=np.sin(th)
plt.plot(x,y,"-k",linewidth=1)
s=signal.dlti(b,a)
t,y=signal.dimpulse(s,n=30)

plt.subplot(122)
plt.stem(t, np.squeeze(y))
plt.title('单位脉冲响应h(n)',fontproperties=font_set)
plt.xlabel('n')
plt.ylabel('h(n)')
plt.grid('on')
plt.show()

程序运行结果如下图所示：

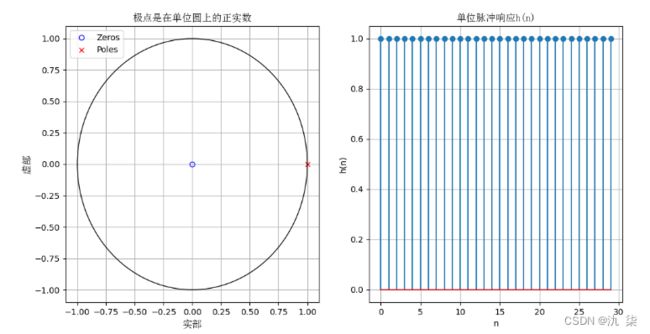
【例7】 画出下列系统函数的零极点分布图、以及对应的时域单位脉冲响应 的波形，并分析系统函数的极点对时域波形的影响。

（1）

（2）

第（1）小题程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
from matplotlib.font_manager import FontProperties

font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
b=[1,0]
a=[1,-1]
z,p,k=signal.tf2zpk(b,a)
print('零点是',z)
print('极点是',p)
print('增益系数为',k)
plt.figure(figsize=(12,6))
plt.subplot(121)
plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
plt.plot(np.real(p), np.imag(p), 'xr')
plt.legend(['Zeros', 'Poles'],loc=2)
plt.title('极点是在单位圆上的正实数',fontproperties=font_set)
plt.xlabel('实部',fontproperties=font_set)
plt.ylabel('虚部',fontproperties=font_set)
plt.grid('on')

th=np.linspace(0,2*np.pi,300)
x=np.cos(th)
y=np.sin(th)
plt.plot(x,y,"-k",linewidth=1)

s=signal.dlti(b,a)
t,y=signal.dimpulse(s,n=30)
plt.subplot(122)
plt.stem(t, np.squeeze(y))
plt.title('单位脉冲响应h(n)',fontproperties=font_set)
plt.xlabel('n')
plt.ylabel('h(n)')
plt.grid('on')
plt.show()

程序运行结果如下图所示：

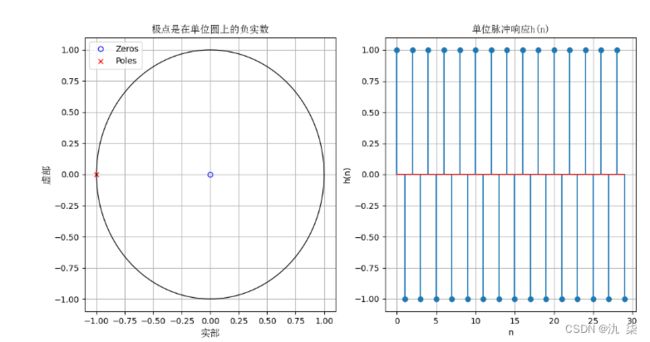
第（2）小题程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
from matplotlib.font_manager import FontProperties

font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
b=[1,0]
a=[1,1]
z,p,k=signal.tf2zpk(b,a)
print('零点是',z)
print('极点是',p)
print('增益系数为',k)
plt.figure(figsize=(12,6))
plt.subplot(121)
plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
plt.plot(np.real(p), np.imag(p), 'xr')
plt.legend(['Zeros', 'Poles'],loc=2)
plt.title('极点是在单位圆上的负实数',fontproperties=font_set)
plt.xlabel('实部',fontproperties=font_set)
plt.ylabel('虚部',fontproperties=font_set)
plt.grid('on')

th=np.linspace(0,2*np.pi,300)
x=np.cos(th)
y=np.sin(th)
plt.plot(x,y,"-k",linewidth=1)

s=signal.dlti(b,a)
t,y=signal.dimpulse(s,n=30)
plt.subplot(122)
plt.stem(t, np.squeeze(y))
plt.title('单位脉冲响应h(n)',fontproperties=font_set)
plt.xlabel('n')
plt.ylabel('h(n)')
plt.grid('on')
plt.show()

程序运行结果如下图所示：

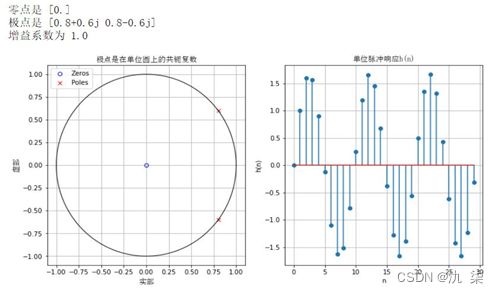
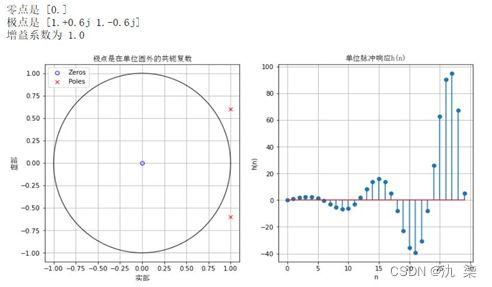
【例8】 画出下列系统函数的零极点分布图、以及对应的时域单位脉冲响应 的波形，并分析系统函数的极点对时域波形的影响。

程序代码略。

程序结果分别如图(a)、(b)、©、(d)所示。
( a)

( b)

( c)

( d)

从以上结果可知，当极点位于单位圆内时，h(n)为衰减序列；当极点位于单位圆上时， h(n)为等幅序列；当极点位于单位圆外时， h(n)为增幅序列。若h(n)有一阶实数极点，则h(n)为指数序列；若h(n)有一阶共轭极点，则h(n)为指数振荡序列；若h(n)的极点位于虚轴左边，则h(n)序列按一正一负的规律交替变化。