常见深度学习算法总结
一、简介
基于深度学习的算法研究是近些年的研究热点,不同领域的研究人员将深度学习应用到不同领域的实际应用中,如图像识别、自然语言处理、推荐系统等,都取得了显著的成果。本文主要介绍常用的深度学习算法,并尝试分析它们之间异同。
二、算法介绍
2.1 神经网络

Neural Networks,简称NN。针对机器学习算法需要领域专家进行特征工程,模型泛化性能差的问题,提出了NN可以从数据的原始特征学习特征表示,无需进行复杂的特征处理。其原理可以使用线性回归理解:
y = W x + b y=Wx+b y=Wx+b,
神经网络中的每一层都是在维护一个参数矩阵W和偏置向量b。模型首先通过样本每一层的前向过程得到预测值,然后计算预测值与真实值之间的误差,最后将误差进行反向传播来更新每一层的W和b, 使之更为更拟合数据集的样本分布。NN相对于机器学习算法的优势在于:可以通过多个层叠加来学习更复杂的特征关系,如异或。
2.2 卷积神经网络
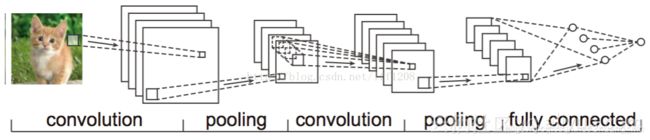
Convolutional Neural Networks, 简称CNN。针对NN存在的密集连接和网络参数过多的问题,提出了CNN进行优化。CNN首先将参数矩阵按照不同的作用分为几个类别:卷积层Convolutional Layer (CONV),池化层Pooling Layer (POOL), 全连接层Fully Connected Layer (FC),来引入参数共享机制Parameter Sharing和连接稀疏性Sparsity of Connections的特性。概念解释:
CONV:用于提取样本中的局部特征
POOL:用于将CONV的结果进行再提取,只提取一定区域的主要特征,以减少参数数量,防止模型过拟合。同时扩大感受野,减少冗余:因为在CONV滑动的时候有大量的重叠区域,导致卷积值存在冗余。
Filter:一般由CONV和POOL组成,从将样本输入特征到变为局部输出。
FC:用于将多个CONV提取到的局部特征及进行拼接,得到一个全局特征用于分类。
Parameter Sharing:对于每个Filter对不同的区域进行卷积时,都用了同一个参数矩阵,因此可以认为这个参数矩阵在全局特征间共享。它使得网络的参数数目大大减少,因而可以使用较少的参数训练出更好的模型,同时还能避免过拟合。
平移不变性:由于Filter的参数共享,我们从全局提取了相似的局部特征,如边界就会在图片的上下左右出现多次,就认为通过Filter的提取,我们将相似的特征平移到一起,照样能识别出特征。
Sparsity of Connections:每个Filter的输出只跟输入样本的一部分特征相关,而相比于NN都是全连接导致的输出的每个单元都受到输入样本每个特征影响,这使得识别效果下降。通过Fitler,我们让每个区域都由专属的Filter得到专属的特征,而规避了其他区域的影响。
使用式子进行理解:
单个卷积核得到的局部特征: c i = W i x + b i c_i=W_ix+b_i ci=Wix+bi,
全局特征通过将多个卷积核的局部特征拼接起来: c = [ c 1 , c 2 , . . . , c n ] c=[c_1, c_2, ..., c_n] c=[c1,c2,...,cn]。
2.3 循环神经网络
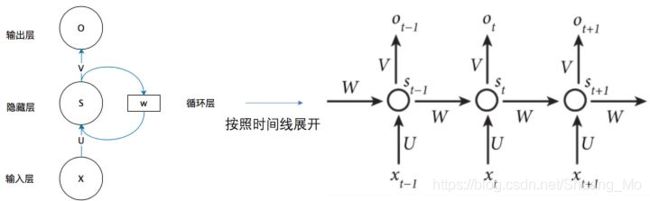
Recurrent Neural Networks,简称RNN。针对NN没有考虑时序信息的问题,即NN对每个样本都是单独处理而没有考虑前后两个样本之间的关系,在具有时序信息的数据中无法捕获到时序信息。在NLP任务中,前后两个输入是有顺序关系的,比如理解一句话的意思时,我们并非将每个词孤立的理解,而是充分考虑每个词之间的关系来理解。处理视频数据的时候,也不会单独处理某一帧,而是分析这些帧连接起来的整个序列。
而RNN通过将上一个训练步的隐藏状态加入到本次的隐藏状态更新中来捕获时序信息,使用公式理解:
RNN在t时刻(训练步)接收到输入x后的输出为:
o t = f ( V ⋅ s t ) o_t=f(V·s_t) ot=f(V⋅st),
其中 s t s_t st表示t时刻隐藏层的值,通过如下方式计算:
s t = g ( U ⋅ x t + W ⋅ s t − 1 ) s_t=g(U·x_t + W·s_{t-1}) st=g(U⋅xt+W⋅st−1),
总的RNN公式表示为 :
o t = f ( V ⋅ g ( U ⋅ X t + W ⋅ s t − 1 ) ) o_t=f(V·g(U·X_t+W·s_{t-1})) ot=f(V⋅g(U⋅Xt+W⋅st−1)),
U,V为参数矩阵,f(.), g(.)为激活函数。
2.4 注意力机制
Attention Mechanism,简称ATT。针对RNN并行度不高以及捕获特征间长距离依赖关系的能力比较弱的问题,提出了ATT。ATT一般可以描述为根据Query与键值对集合key-value中的Key的相似度得到多个values并取它们的加权得到输出结果,计算过程分为三步走:
1)比较Q和K的相似度:
f ( Q , K i ) , i = 1 , 2 , 3 , . . . f(Q, K_i), i=1, 2, 3,... f(Q,Ki),i=1,2,3,...
2)将1)得到的相似度进行归一化:
3)使用2)计算得到的权重对所有values进行加权求和,得到经过Attention处理后的向量:
∑ i = 1 m α i V i \sum_{i=1}^m\alpha_iV_i ∑i=1mαiVi.
计算相似度的方法分为三种:
1)点乘: f ( Q , K i ) = Q T K i f(Q, K_i)=Q^TK_i f(Q,Ki)=QTKi,
2)权重: f ( Q , K i ) = Q T W K i f(Q, K_i)=Q^TWK_i f(Q,Ki)=QTWKi,
3)拼接权重: f ( Q , K i ) = W [ Q T ; K i ] f(Q, K_i)=W[Q^T;K_i] f(Q,Ki)=W[QT;Ki],
4)感知器: f ( Q , K i ) = V T t a n h ( W Q + U K i ) f(Q, K_i)=V^Ttanh(WQ+UK_i) f(Q,Ki)=VTtanh(WQ+UKi),
即使用三个参数矩阵学习相似度关系
2.4.1 缩放点乘注意力
Scaled Dot-Product Attention,具体计算过程为:
Q = X W Q , K = X W K , V = X W V , Z = α i V = s o f t m a x ( Q K T ( d k ) , Q=XW_Q, K=XW_K, V=XW_V, Z=\alpha_iV=softmax(\frac{QK^T}{\sqrt(d_k)}, Q=XWQ,K=XWK,V=XWV,Z=αiV=softmax((dk)QKT,其中, W Q , W K , W V W_Q,W_K,W_V WQ,WK,WV分别为Q,K,V的embedding矩阵,使得使用相同的输入X得到不同的embedding, d k d_k dk是规范化因子,用来按行进行归一化(计算Q中的每个query和K中所有keys的相似度),Z是经过attention处理的X。
2.4.2 自注意力
Self-Attention,如在NLP中,文本词向量自己和自己做attention,即每个词都要和所有词计算attention,而且不论两个词在一段话中的距离有多长,最大路径长度就只是1(即attention分数为1),从而能捕获到长距离的依赖关系。
2.4.3 多头注意力
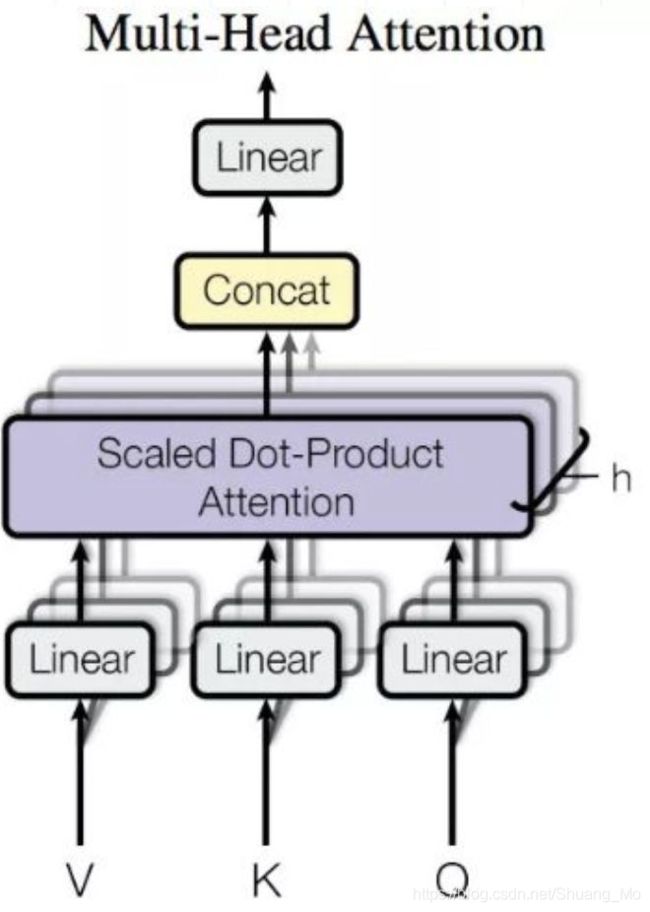
Multi-Head Attention,可视为attention的ensemble版本,不同的head学习不同的子空间语义。其实质就是将缩放点乘注意力的过程做H次,然后把H次的输出和起来:上述计算的到Q,K,V切分(分割列/特征)为H份,作为不同的Head学习注意力。因为经过多个Head的embedding会导致特征维度变多,因此还需要一个参数矩阵W转换为与输入X相同的维度。
2.5 图神经网络
Graph Neural Networks,简称GNN。首先明确图数据结构的两种特征:
1 图的结构关系:图中每个顶点的邻居(边)
2 顶点特征:每个顶点自身的属性(点)
图神经网络的本质都是将邻居顶点的特征聚合到中心顶点上,利用图的局部位置信息(邻接关系)学习新的特征表达,根据不同的聚合方式分为两种:GCN利用了拉普拉斯矩阵,GAT利用了Attention机制。
此外,需要注意的是GNN主要用于学习拓扑图的信息,但本身对节点特征的学习能力不足,因此在一般而言,节点的特征都是经过其他模型如CNN,RNN等转换为线性可分的embedding后再作为节点的属性。
2.5.1 图卷积神经网络
Graph Convolutional Networks,简称GCN。针对CNN只能解决欧式结构数据的问题,即CNN要求数据能够排列成很整齐的矩阵才能进行卷积计算。而对于非欧式数据,如拓扑图中每个顶点的邻居数目不固定,从而无法保持平移不变性,因而提出了GCN。GCN主要分为两种:
1 空域:称为顶点域,该方法需要明确两个问题:如何确定感受野,按照何种方式每个顶点不同邻居数目特征。因为它对每个顶点单独处理它的邻居特征,导致计算复杂度高,而且特征提取效果不好【原因暂时未知】。
2 谱域:该方法首先将数据中的拓扑关系,即拓扑图中的每个顶点间的连接关系进行傅里叶变换从而转换到谱域中,在谱域中拓扑关系变为了欧式结构进而能够进行卷积操作,随后对卷积结果进行傅里叶逆变换就得到了想要的结果。
GCN与CNN的异同:首先数据结构有区别;但同样具有稀疏连接/局部连接性(第二代GCN)和参数共享。
2.5.2 图注意神经网络
Graph Attention Networks,简称GAT。针对GCN无法进行indective任务,即训练阶段与测试阶段要处理的图不同,也就是动态图问题;以及普通GCN只能作用与无向图,无法处理有向图的问题。它的计算过程与所有Attention机制相同,分为两步:
1 计算注意力系数:对每个顶点分别计算它的邻居与自己的相似系数,该相似系数归一化后就得到了注意力系数
2 加权求和:根据1得到的注意力系数对所有的邻居特征进行加权求和,得到最终的聚合信息
三、深度学习的特点
3.1 模型设计原则
因为深度学习的出现就是尽可能的避免特征工程,将主要精力放到模型的结构设计和调参中。模型的结构设计需要结合数据不同方面的特征进行考虑,如CNN侧重于提取空间特征,RNN侧重于提取时序特征,Attention侧重提取数据的全局特征,GNN侧重提取非欧数据的特征等。
3.2 模型调参
模型调参是在模型结构设计完成之后,尽可能的提升模型的效果,主要有几个参数:学习率即梯度更新的快慢,梯度更新算法即如何更新你的梯度,有包括传统的 SGD,Momentum SGD,AdaGrad,RMSProp 和 Adam 等等。
四、总结
不同的深度学习算法有着有着各自优势和特点,没有孰优孰劣之分,我们应该做的是基于不同的业务场景,充分理解业务数据,然后使用适合的深度学习技术实现最佳的效果。其次,深度学习和机器学习的模型和算法,并不是说只要使用最先进、最复杂的模型就能就一定能解决问题,本质上来说计算机技术只是辅助人进行决策,或者将人的决策过程自动化、提升效率,因此模型只选最适合的,而不是最复杂的。