时间最优轨迹规划（3-5-3次多项式）

轨迹规划是指机械臂在给定起始点和终止点之间运动，其中要保持时间和能量的双重最优，就需要对路径之间的插值点进行规划，目前比较常见的就是三次多项式、五次多项式以及B样条插值等进行轨迹规划。轨迹优化是指对路径上的时间和能量进行优化，本文将介绍五自由度的机械臂时间最优轨迹规划，使用粒子群算法对轨迹进行优化。

1. 多项式插值算法

1.1 三次多项式插值

三次多项式插值顾名思义，就是使用三次多项式对机械臂的初始点和终止点之间进行插值，将关节角和时间写成函数$\theta \left(t\right)$，使该函数依次通过各个路径点，下面是三次多项式的表达式：
$$\theta \left(t\right)=a_0+a_{1}t+a_2{t}^2+a_3{t}^3\text{\hspace{1em}(1)}$$
由于机器人的初末位置的速度为0，则：
$$\{\begin{array}{l}\theta \left(0\right)={\theta }_0\\ \theta \left(t_f\right)={\theta }_f\\ \dot{\theta }\left(0\right)=0\\ \dot{\theta }\left(t_f\right)=0\end{array}\text{\hspace{1em}(2)}$$
其中$t_f$表示结束时间。运动轨迹上的关节速度和加速度为：
$$\{\begin{array}{l}\dot{\theta }\left(t\right)=a_1+2{\dot{a}}_2{t}^2+3a_3{t}^3\\ \ddot{\theta }\left(t\right)=2a_2+6a_{3}t\end{array}\text{\hspace{1em}(3)}$$
将始末速度和加速度带入到公式（1）和公式（3）里面会得到：
$$\{\begin{array}{l}{\theta }_0=a_0\\ {\theta }_f=a_0+a_1{t}_f+a_2{t}_f^2+a_3{t}_f^3\\ 0=a_1\\ 0=a_1+2a_2{t}_f+3a_3{t}_f^3\end{array}\text{\hspace{1em}(4)}$$
求解上述线性方程组可得：
$$\{\begin{array}{l}{a}_0={\theta }_0\\ a_1=0\\ a_2=\frac{3}{t_f^2}\left({\theta }_f-{\theta }_0\right)\\ a_3=-\frac{2}{t_f^3}\left({\theta }_f-{\theta }_0\right)\end{array}\text{\hspace{1em}(5)}$$
这里可以使用$mathematica$进行求解：

因此，三次多项式插值函数表示为：
$$\theta \left(t\right)={\theta }_0+\frac{3\left({\theta }_f-{\theta }_0\right)}{t_f^2}{t}^2-\frac{2\left({\theta }_f-{\theta }_0\right)}{t_f^3}{t}^3$$

1.2 过路径点的三次多项式插值

当插值点为多个时，可以将路径点中的两个靠近的插值点作为“起始点”和“终止点”，但不是真正的“起始点”和“终止点”，此时的关节速度肯定是不为零的，此时的速度约束条件可以写成：
$$\{\begin{array}{l}\dot{\theta }\left(0\right)={\dot{\theta }}_0\\ \dot{\theta }\left(t_f\right)={\dot{\theta }}_f\end{array}\text{\hspace{1em}(6)}$$
带入到公式（1）和（3）可知：
$$\{\begin{array}{l}{\theta }_0=a_0\\ {\theta }_f=a_0+a_1{t}_f+a_2{t}_f^2+a_3{t}_f^3\\ {\dot{\theta }}_0=a_1\\ {\dot{\theta }}_f=a_1+2a_2{t}_f+3a_3{t}_f^3\end{array}\text{\hspace{1em}(7)}$$
求解方程组（7）得：
$$\{\begin{array}{l}{a}_0={\theta }_0\\ a_1={\dot{\theta }}_0\\ a_2=\frac{3}{t_f^2}\left({\theta }_f-{\theta }_0\right)-\frac{2}{t_f}{\dot{\theta }}_0-\frac{1}{t_f}{\dot{\theta }}_f\\ a_3=-\frac{2}{t_f^3}\left({\theta }_f-{\theta }_0\right)-\frac{1}{t_f^2}\left({\dot{\theta }}_0+{\dot{\theta }}_f\right)\end{array}\text{\hspace{1em}(8)}$$
同样，这里也可以使用$mathematica$进行求解：

1.3 五次多项式插值

对于要求加速度约束时，三次多项式已经不能满足要求了，因此就需要五次多项式进行插值，五次多项式的表达式为：
$$\theta \left(t\right)=a_0+a_{1}t+a_2{t}^2+a_3{t}^3+a_4{t}^4+a_5{t}^5\text{\hspace{1em}(9)}$$
五次多项式需满足6个约束条件：
$$\{\begin{array}{l}{\theta }_0=a_0\\ {\theta }_f=a_0+a_1{t}_f+a_2{t}_f^2+a_3{t}_f^3+a_4{t_f}^4+a_5{t_f}^5\\ {\dot{\theta }}_0=a_1\\ {\dot{\theta }}_f=a_1+2a_2{t}_f+3a_3{t}_f^2+4a_4{t}_f^3+5a_5{t_f}^4\\ {\ddot{\theta }}_0=2a_2\\ {\ddot{\theta }}_f=2a_2+6a_3{t}_f+12a_4{t}_f^2+20a_5{t}_f^3\end{array}\text{\hspace{1em}(10)}$$
解上述线性方程组得：
$$\{\begin{array}{l}{a}_0={\theta }_0\\ a_1={\dot{\theta }}_0\\ a_2=\frac{{\ddot{\theta }}_0}{2}\\ a_3=\frac{20{\theta }_f-20{\theta }_0-\left(8{\dot{\theta }}_f+12{\dot{\theta }}_0\right)t_f-\left(3{\ddot{\theta }}_0-{\ddot{\theta }}_f\right)t_f^2}{2t_f^3}\\ a_4=\frac{30{\theta }_0-30{\theta }_f+\left(14{\dot{\theta }}_f+16{\dot{\theta }}_0\right)t_f+\left(3{\ddot{\theta }}_0-2{\ddot{\theta }}_f\right)t_f^2}{2t_f^4}\\ a_5=\frac{12{\theta }_f-12{\theta }_0-\left(6{\dot{\theta }}_f+6{\dot{\theta }}_0\right)t_f-\left({\ddot{\theta }}_0-{\ddot{\theta }}_f\right)t_f^2}{2t_f^5}\end{array}\text{\hspace{1em}(11)}$$
使用$mathematica$进行求解：

2. 多项式函数的构造（3-5-3）

下面将介绍使用3-5-3次多项式对五自由度机械臂进行插值，设置4个插值点，用过逆运动学方程求解得到各个关节在各个差值点的关节角度，用${\theta }_{ij}$表示关节$i$插值的角度，其中$i$表示关节数$(i=1,2,3,4,5)$,$j$表示差值点的序号$(j=1,2,3,4)$。
第$i$关节3-5-3样条多项式的通式为：
$$\{\begin{array}{l}{l}_{j1}\left(t\right)=a_{j13}{t}^3+a_{j12}{t}^2+a_{j11}t+a_{j10}\\ l_{j2}\left(t\right)=a_{j25}{t}^5+a_{j24}{t}^4+a_{j23}{t}^3+a_{j22}{t}^2+a_{j21}t+a_{j20}\\ l_{j3}\left(t\right)=a_{j33}{t}^3+a_{j32}{t}^2+a_{j31}t+a_{j30}\end{array}\text{\hspace{1em}(12)}$$
其中$l_{j1}(t)$，$l_{j2}(t)$，$l_{j3}(t)$分别代表3-5-3样条多项式的轨迹，多项式中的系数$a$可根据约束条件求出，并根据约束条件和约束边界可求出矩阵$A$，且约束条件和约束边界只与时间$t$有关。系数$a$可由式（13）（14）和（15）求出。式（13）的$t_1$，$t_2$，$t_3$分别表示第$i$关节的3段多项式插值的时间，式（14）表示关节角的位移矩阵，式（15）即系数$a$的求解方程式。其中，$x_{ij}$表示第$i$个关节第$j$段插值的位移，已知第$i$个关节各段的初始点$x_{j0}$，连个路径点$x_{j1}$和$x_{j2}$、终止点$x_{j3}$的位移，路径点之间的位移、速度和加速度连续以及初始点和终止点的速度（一般为0）、加速度。
$$A=\left[\begin{array}{cccccccccccccc}{t}_1^3& t_1^2& t_1& 0& 0& 0& 0& 0& -1& 0& 0& 0& 0& 0\\ 3t_1^2& 2t_1& 1& 0& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0\\ 6t_1& 2& 0& 0& 0& 0& -2& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& t_2^5& t_2^4& t_2^3& t_2^2& t_2& 1& 0& 0& 0& 0& -1\\ 0& 0& 0& 5t_2^4& 4t_2^3& 3t_2^2& 2t_2& 1& 0& 0& 0& 0& -1& 0\\ 0& 0& 0& 20t_2^3& 12t_2^2& 6t_2& 2& 0& 0& 0& 0& -2& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& t_3^3& t_3^2& t_3& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 3t_3^2& 2t_3^1& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 6t_3& 2& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0\end{array}\right]\text{\hspace{1em}(13)}$$
$$\theta ={\left[\begin{array}{cccccccccccccc}0& 0& 0& 0& 0& 0& x_{j3}& 0& 0& x_{j0}& 0& 0& x_{j2}& x_{j1}\end{array}\right]}^T\text{\hspace{1em}(14)}$$
$$a=A^{-1}\theta ={\left[\begin{array}{cccccccccccccc}{a}_{j13}& a_{j12}& a_{j11}& a_{j10}& a_{j25}& a_{j24}& a_{j23}& a_{j22}& a_{j21}& a_{j20}& a_{j33}& a_{j32}& a_{j31}& a_{j30}\end{array}\right]}^T\text{\hspace{1em}(15)}$$

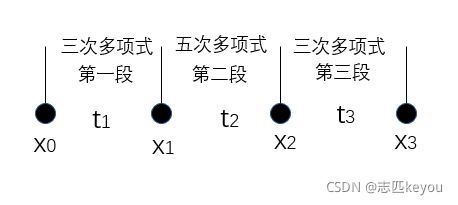
首先解释以下矩阵$A$所表示的含义:
所谓的3-5-3多项式规划所表示的就是，在关节规划中，关节在时间$t_1$使用三次多项式进行规划，在时间$t_2$使用五次多项式进行规划，在时间$t_3$使用三次多项式规划。式（15）也可以写成$Aa=\theta$，因此可以对应矩阵相乘得到$\theta$矩阵，首先是矩阵$A$的前三行与矩阵$a$相乘，可以发现第一行是三次多项式的位移，后面还有个$-1$是五次多项式当时间等于0时的位移；第二行是加速度，同样后面的$-1$是五次多项式当时间等于0时的速度；第三行是加速度，后面的$-2$是五次多项式当时间等于0时的加速度。同理第四至第六行也是一样。第七行至第九行是所谓的第三段，因此都没有减去$1$或者$2$，因此位移就等于$x_{j3}$。第十行表示的是$a_{j10}=0$，是在初始点时，时间为零，因此第一段的位移也为零，在三次多项式规划中，当时间为零时就可以得到此式。第十一行表示的是$a_{j11}=0$，在第一段三次多项式规划中，当时间为零时带入速度函数就可以得到此式。第十二行表示的是$a_{j12}=0$，在第一段三次多项式规划中，当时间为零时带入加速度函数就可以得到此式。第十三行表示的是$a_{j30}=x_{j2}$，在第三段三次多项式规划中，当时间为零时带入位移函数就可以得到此式。第十四行表示的是$a_{j20}=x_{j1}$，在第三段三次多项式规划中，当时间为零时带入位移函数就可以得到此式。

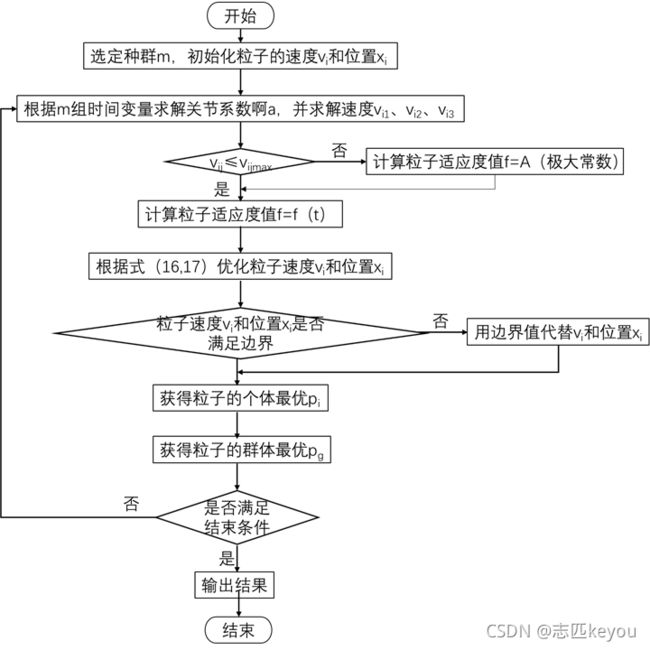
3. 基于PSO求解时间最优问题

粒子群优化算法（PSO）是一种智能的全局优化算法，它是根据鸟群在捕食过程中的个体之间的相互协作的启发，从而发明的一种优化算法。

在粒子群算法中，每一个粒子都有一个位置属性（$x_i$）和一个速度属性($v_i$)，位置属性就是表面的意思，就是粒子所处的位置，速度属性是粒子飞行的速度和距离，把需要优化的变量看做是粒子，所有的粒子都有一个由被优化的函数决定的适应值，通过粒子适应值的大小来决定最优的值。

在粒子群算法中随即给出一群粒子，通过循环迭代寻求最优解，在每次迭代过程中，粒子通过跟踪两个“位置”来更新自己，第一个“位置”是微粒$i$本身目前所经历的最好的位置，为$p_i$，第二个“位置”是群体微粒目前所经历的最好的位置，为$p_g$。在没有找到两个最优解时，粒子根据式（16）、式（17）来更新自己的速度和位置。

$$v_{id}^{k+1}=\omega \times v_{id}^k+c_1\times r_1\times (p_{id}-x_{id}^k)+c_2\times r_2\times (p_{gd}-x_{id}^k)\text{\hspace{1em}(16)}$$
$$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1}\text{\hspace{1em}(17)}$$
其中，惯性权重$\omega$的求解公式为$\omega =W_{max}-i(W_{max}-W_{min})/N_{max}$，$W_{max}=0.9$为最大惯性权重，$W_{min}=0.4$为最小惯性权重，$N_{max}=50$为最大迭代数目，$i$为迭代次数，$d$表示设计参数的维度，$c_1=2$与$c_2=2$为学习因子，$r_1$和$r_2$为$[0,1]$之间随机任意值，各个粒子的位置$x_{id}\in [-x_{\max },x_{\max }]$各个粒子的速度$v_{id}\in [-v_{\max },v_{\max }]$，任意随机产生的粒子的$x_{id}$和$v_{id}$都要符合该约束条件，如果随机产生的粒子$x_{id}$和$v_{id}$不符合约束条件，就用边界值代替。式（16）为粒子的速度更新函数，等号右边的第一项是之前的速度乘以惯性权重，第二项是微粒本身位置的优化，第三项是微粒在全局中的位置优化，式（17）为粒子的位置更新函数。

就这么说吧，就是在一定的范围内随机的产生很多粒子，这些粒子就会有自己的位置，然后这些粒子就会根据自己的位置寻找最优的位置（也就是最优解），但是怎么去寻找最优解，就是让这些粒子动起来，要使这些粒子动起来就有一个问题，就是怎么动，就要定义一个速度，这里的速度不仅有大小还有方向，所以就有式（16）所表示的速度更新函数，这里的速度更新函数就是根据上一次的速度乘以惯性权重、自身的位置所经历的最佳位置减去上一次的位置和所有粒子经历过的最佳位置减去上一次的位置，当然这里最佳的位置是根据适应度函数来决定的，还要乘以学习因子和随机数，直到找到最优的位置，或者就是当迭代的次数达到最大，完成整个迭代过程。一般在最大迭代次数之前就会有最佳的适应值。

当优化轨迹的时候，将待优化多项式的系数看做是待优化量，根据式（13）（也就是$A$矩阵）得到时间变量$t$，如果直接选择时间变量$t$搜索空间进行优化，可以将维数降到最低，这样就可以使得计算量大大的减小，也减小了粒子群算法寻优的复杂性和困难性。用粒子群算法对机器人末端的轨迹进行优化，这时的搜索空间维数为3，轨迹优化的最终目标是在满足动力学约束的条件下，所有关节运动的时间最短，因此适应度函数就为：
$$f(t)=min(t_{i1}+t_{i2}+t_{i3})\text{\hspace{1em}(18)}$$
$$\max \left\{\left|v_{ij}\right|\right\}\le v_{ij\max }\text{\hspace{1em}(19)}$$
$v_{ij}$和$v_{ijmax}$分别是第$i$个关节的实时速度和最大限制速度，利用粒子群算法可以对上面的问题进行解决。
这里的$i$指的是第几关节，$i=1,2,3,4,5$
这里的$j$指的是插值点的序号，$j=1,2,3,4$，一共是四个插值点，从上面的图中也可以看出来。

利用粒子群算法对机器人末端轨迹进行时间最短轨迹优化的方法：首先对机械臂的每个关节进行时间最短优化，然后对优化后的各个关节运动轨迹进行整体的优化，从而得到机械臂最终的时间最短轨迹优化路径。

利用粒子群算法对机器人第$i$个关节进行时间最优规划，通过粒子群优化循环迭代可以得到每个关节的时间最优轨迹，再把每个关节得到的结果用粒子群优化算法进行优化，可以得到机械臂整体的最优轨迹。

4. 进行仿真

仿真的话还是基于前面章节提到的5自由度机器人进行位置控制，根据逆运动学可以解出四个插值点所对应的关节的角度值，这里只对前三个关节进行求解。

起始点	路径点1	路径点2	终止点
（0,-800,-400）	(200,-300,-300)	(400,100,-300)	(500,300,-200)

关节	${\theta }_{j0}$	${\theta }_{j1}$	${\theta }_{j2}$	${\theta }_{j3}$
关节1	0	-56.3099	14.0362	30.9638
关节2	0	4.1328	-1.1667	-22.5516
关节3	0	113.0098	110.4723	102.1321

根据粒子群算法，在不同的速度约束下，对关节1进行优化，求解最优时间，对群体最优粒子的位置$p_g$进行每次迭代的记录，绘制图形，从而得到不同速度约束下，群体最优粒子的位置$p_g$变化图。

优化程序：

%粒子群优化算法:
%主函数源程序
clc
clear all;
clc;
m = 20;      %初始化20个随机粒子
D = 3;   %维度，就是这里对三个参数进行寻优 
pgf(1) = 100;   %给定的最大的适应度值
Wmax = 0.9;
Wmin = 0.4;
cl = 2;
c2 = 2;
Nmax = 50 ;  %最大迭代次数

for i = 1:m
    for j = 1:D
        x(i,j) = rand * (4.0-0.1)+0.1;    % 首先随机生成20行3列的矩阵，也就是所谓的初始化种群
        v(i,j) = -2+4 * rand;  %初始化速度，为一个粒子有一个初始速度
    end
    px(i,:) = x(i,:);   %每个粒子最优位置
    pf(i) = fitness(x(i,1),x(i,2),x(i,3),D)   %每个粒子的最优位置的适应度
    if pgf(1) > pf(i)           
        pgx = x(i,: );          
        pgf(1) = pf(i);       
    end
end

for i = 1:m        
    a(:,i) = Aa(x(i,1),x(i,2) ,x(i,3));    %将初始化的粒子带入到Aa函数里面求出a的值
    jv(1,i) = 3 * a(1,i) * x(i,1)^2+ 2 * a(2,i) * x(i,1)+a(3,i);
    jv(2,i) = 5 * a(5,i) * x(i,2)^4 +4 * a(6,i) * x(i,2)^3+ 3 * a(7,i) * x(i,2)^2+2* a(8,i) * x(i,2)+ a(9,i);
    jv(3,i) = 3 * a(11,i)* x(i,3)^2+ 2 * a(12,i) * x(i,3)+ a(13,i);    %求出每个关节的速度
    if jv(1,i)<=( -20 * pi/180)|jv(1,i)>= (20 * pi/180)|jv(2,i)<=( -20 * pi/180)|jv(2,i)>=(20 * pi/180)|jv(3,i)<=( -20 * pi/180)|jv(3,i)>=(20 * pi/180)    %将每个关节的速度限制在-20到20之间
        f = 100;                         
    else
        f = fitness(x(i,1 ),x(i,2),x(i,3),D); %总时间
    end
    if pf(i) > f
        px(i,:) = x(i,:);
        pf(i) = f;
    end
    if pgf > pf(i)
        pgf = pf(i);
        pgx = x(i,: );
    end
end

for k = 2:50    %迭代的次数
    pgf(k) = pgf(k - 1);
    w = (Wmax - k * ( Wmax - Wmin)/ Nmax) ;
    for i = 1:m
        for j= 1 : D
            v(i,j)= w * v(i,j)+ cl * rand * (px(i,j)- x(i,j))+ c2 * rand * (pgx(j)-x(i,j));
            if v(i,j)<-2
                v(i,j)= -2;
            end
            if v(i,j)>2
                v(i,j)= 2;
            end
            x(i,j) = x(i,j)+v(i,j)
            if x(i,j)<0.1
                x(i,j)= 0.1;
            end
            if x(i,j)>4
                x(i,j) = 4;
            end
        end
        a( : ,i) = Aa(x(i,1),x(i,2),x(i,3));
        jv(1,i)= 3 * a(1,i) * x(i,1)^2+ 2* a(2,i) * x(i,1)+ a(3,i);
        jv(2,i) = 5 * a(5,i) * x(i,2)^4+ 4 * a(6,i) * x(i,2)^3+ 3 * a(7,i) * x(i,2)^2+2*a( 8,i) * x(i,2) + a(9 ,i);
        jv(3,i) = 3 * a(11,i) * x(i,3)^2+ 2* a(12,i) * x(i,3)+ a(13,i);
        if jv(1,i)<= ( -20 * pi/180)|jv(1,i)>= (20 * pi/180)|jv(2,i)<=( -20 * pi/180)|jv(2,i) >=(20 * pi/180)|jv(3,i)<=( -20 * pi/180)|jv(3,i) >=(20 * pi/180)
            f = 100;
        else
            f = fitness(x(i,1),x(i,2),x(i,3),D);
        end
        if pf>f
            px(i,:) = x(i,:);
            pf(i) = f;
        end
        if pgf(k) > pf(i)
            pgf(k) = pf(i);
            pgx = x(i,:);
        end
    end
end

%适应度函数源程序(fitness.m)
function result = fitness(t1,t2,t3,D)
    sum = t1 + t2 + t3;
    result = sum ;
end

%多次多项式系数a求解程序(Aa. m)
function H = Aa(t1,t2,t3,D)
    x3 = 102.1321 * pi/180;
    x2 = 110.4723 * pi/180;
    x1 = 113.0098 * pi/180;
    x0 = 0;
    format long
    A=[t1^3   ,t1^2,t1,1 ,0      ,0       ,0    ,0   , 0,-1, 0   ,0   ,0  ,0;
        3*t1^2,2*t1,1 ,0 ,0      ,0       ,0    ,0   ,-1, 0, 0   ,0   ,0  ,0;
        6*t1  ,2   ,0 ,0 ,0      ,0       ,0    ,-2  , 0, 0, 0   ,0   ,0  ,0;
        0     ,0   ,0 ,0,t2^5    ,t2^4   ,t2^3  ,t2^2,t2, 1 ,0,   0   ,0 ,-1;
        0     ,0   ,0 ,0,5*t2^4  ,4*t2^3 ,3*t2^2,2*t2,1 , 0, 0,   0   ,-1, 0;
        0     ,0   ,0 ,0,20*t2^3 ,12*t2^2,6*t2  ,2   ,0 , 0, 0,   -2  ,0 , 0;
        0     ,0   ,0 ,0,0       ,0      ,0     ,0   ,0 , 0, t3^3,t3^2,t3, 1;
        0     ,0   ,0 ,0,0       ,0      ,0     ,0   ,0 , 0, 3*t3^2,2*t3,1,0;
        0     ,0   ,0 ,0,0       ,0      ,0     ,0   ,0 , 0, 6*t3,2 ,  0  ,0;
        0     ,0   ,0 ,1,0       ,0      ,0     ,0   ,0 , 0, 0   ,0   ,0 , 0;
        0     ,0   ,1 ,0,0       ,0      ,0     ,0   ,0 , 0, 0   ,0   ,0 , 0;
        0     ,1   ,0 ,0,0       ,0      ,0     ,0   ,0 , 0, 0   ,0   ,0 , 0;
        0     ,0   ,0 ,0,0       ,0      ,0     ,0   ,0 , 0, 0   ,0   ,0 , 1;
        0     ,0   ,0 ,0,0       ,0      ,0     ,0   ,0 , 1, 0   ,0   ,0 , 0];
    b = [0,0,0,0,0,0,x3,0,0,x0,0,0,x2,x1]';
    B = inv(A);
    H = B * b;
end