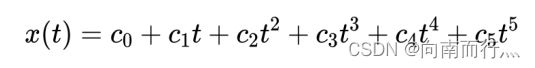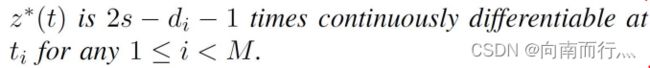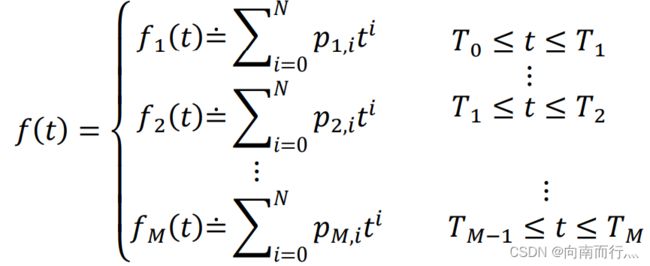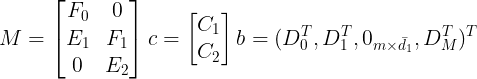轨迹优化——三维空间下通过BVIP生成最小jerk轨迹
写在前面的
这篇文章主要是记录下深蓝学院开的《移动机器人运动规划》这门课程中第五章-最优轨迹生成的作业即三维空间下通过BVIP生成最小jerk轨迹相关的内容及做作业时的过程。
其课程链接在下面，感兴趣的可以去报名学习：
移动机器人运动规划-深蓝学院
任务描述
如下图所示，给定三维空间下起始点和终点的位置、速度和加速度，以及（M-1）个中间位点的位置，那么这段轨迹就被分成了 M 段。其中每小段轨迹移动的时间 
也是给定的。
要求我们用最优条件来计算三维最小jerk轨迹的系数，因为这些系数能描述一条轨迹，这个后面也会讲。
至于最优条件怎么来的，这里就不说明了，后面会讲最优条件是什么。
边界值问题（Boundary value problem，BVP)
在讲BVIP时我们先来讲轨迹生成中的BVP问题，这一部分建议先看下面链接的相关内容：
Robotics: Aerial Robotics（空中机器人）笔记（六）:无人机运动规划
简单来说，就是我们已知机器人初始的状态（比如说初始的位置，速度，加速度等），以及最后的状态，也就是我们只考虑起始和最终的状态，不考虑中间的状态。
如下图所示，这是一个无人机接球的例子，只考虑无人机起始的状态和接球的状态来生成轨迹：
最优条件理论告诉我们：如果我们的输入是轨迹的 s 阶导数（如果是位置的话 s=1 ，加速度的话 s=2， jerk的话 s=3，依此类推），那么其描述轨迹的多项式的阶数就是 2s -1。我们现在要生成是jerk轨迹，那么多项式的阶数就是 2 * 3 - 1 = 5。
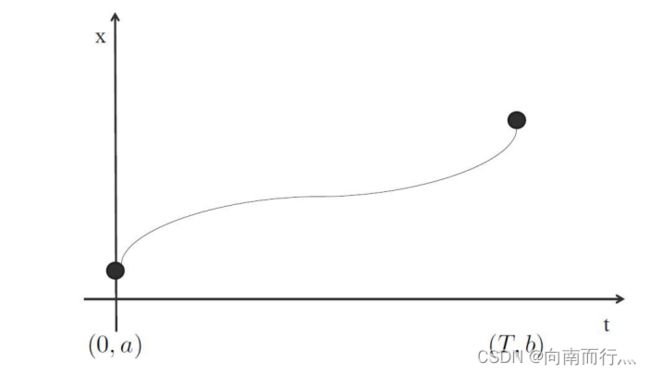
我们来看一维空间的情况，起点和终点的状态已知，求jerk轨迹：
那么我们的jerk轨迹就可以这么描述：
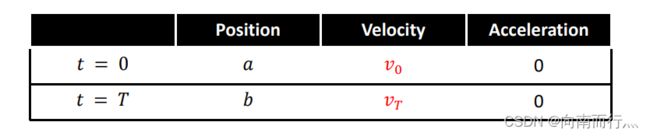
通过将 t=0, t=T代入到上面的多项式，以及多项式的一阶求导，二阶求导可得：
如果边界条件是这样的则是：
这时如果这段轨迹运行的时间 T 已知，那么就可以求出这条轨迹的参数 
了 。那么轨迹也就知道了。
那么如果我们要设计一条经过指定位点的轨迹，我们就需要指定每个位点的状态，包括位置，速度，加速度等等。 但有时候我们只是要让机器人经过某个位点，而不需要规定其在位点的速度，加速度等状态，那么这就是BIVP（Boundary-intermediate value problem）。
BIVP（Boundary-intermediate value problem）
最优条件理论告诉我们，如果我们的输入是轨迹的 s 阶导数，那么其 2s-d-1 阶导数也都是连续可导的。也就是说，如果我们的输入是 jerk（ s = 3 ），首先位置，速度，加速度肯定是连续的，这没有异议。但是包括 jerk 在内，snap（ s = 4 ）在位点上也是连续可导的。
我们知道，轨迹是一个多项式来描述，那么我们就可以通过解下面的线性方程来求解轨迹的系数：
对于最小jerk轨迹，我们把轨迹分成 M 段，每段可以用一个五阶的多项式来描述，通过最优条件理论，即每个位点左右两段轨迹的多阶导数的连续性以及位置的约束来求解轨迹的系数：
我们选择下图上方的 T 描述方式，也就是第二段轨迹的起始时刻为 0 ，这样计算起来数值比较稳定，解得更快。
这样，我们就把轨迹的优化问题转化成了线性方程组的求解问题，接下来我们将以下图为基础开始推导相关变量及编写程序。
公式推导及代码编写
我们的目的就是构建关于时间 T 的 M 矩阵和关于边界值的 b 矩阵，然后通过 M 矩阵的逆来求解系数矩阵 c ：
首先我们初始化两个矩阵，其中 pieceNum 表示的是轨迹的段数，也就是 M，因为我们算的轨迹是三维的，所以边界值的列数为 3 ，代表x，y，z：
Eigen::MatrixXd M = Eigen::MatrixXd::Zero(6 * pieceNum , 6 * pieceNum );
Eigen::MatrixXd b = Eigen::MatrixXd::Zero(6 * pieceNum , 3);接下来我们先把问题缩小，先看由三个点（起始点、终点和一个中间位点）构成的轨迹，注意这里的 
是指系数矩阵：
// coefficientMatrix is a matrix with 6*piece num rows and 3 columes
// As for a polynomial c0+c1*t+c2*t^2+c3*t^3+c4*t^4+c5*t^5,
// each 6*3 sub-block of coefficientMatrix is
// -- --
// | c0_x c0_y c0_z |
// | c1_x c1_y c1_z |
// | c2_x c2_y c2_z |
// | c3_x c3_y c3_z |
// | c4_x c4_y c4_z |
// | c5_x c5_y c5_z |
// -- --我们知道，最小jerk的轨迹是由一个五阶多项式来描述的：
其一阶导的形式：
依此类推：
我们首先知道了起始点的位置，速度和加速度，那么把 t=0代入进去就有:
再看回原式，就有第一个表达式：
其中：
那么我们就可以往 M 矩阵和 b 矩阵填入相应的元素：
Eigen::MatrixXd F_0(3,6);
F_0 << 1, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0,
0, 0, 2, 0, 0, 0;
M.block(0, 0, 3, 6) = F_0;
b.block(0, 0, 3, 3) << initialPos(0), initialPos(1), initialPos(2),
initialVel(0), initialVel(1), initialVel(2),
initialAcc(0), initialAcc(1), initialAcc(2);终止位置也同理，这里我们假设最后一段轨迹的表达式为：
那么就有：
因为我们现在是拿三个点组成的两段轨迹做例子，实际上下标2已经表示最后一段轨迹 M，再看回原式，就有最后一个表达式：
其中：
那么我们又可以往 M 矩阵和 b 矩阵填入相应的元素，相应的代码编写如下，其中 t 就是最后一段轨迹运行的时间：
double t(timeAllocationVector(pieceNum-1));
Eigen::MatrixXd E_M(3,6);
E_M << 1, t, pow(t, 2), pow(t, 3), pow(t, 4), pow(t, 5),
0, 1, 2*t, 3*pow(t, 2), 4*pow(t, 3), 5*pow(t, 4),
0, 0, 2, 6*t, 12*pow(t, 2), 20*pow(t, 3);
M.block(6 * pieceNum -3, 6 * (pieceNum - 1), 3, 6) = E_M;
b.block(6 * pieceNum -3, 0, 3, 3) << terminalPos(0), terminalPos(1), terminalPos(2),
terminalVel(0), terminalVel(1), terminalVel(2),
terminalAcc(0), terminalAcc(1), terminalAcc(2);接下来我们就要考虑中间点的边界条件问题了，此时我们注意到要计算的是：
也就是说，现在我们需要考虑中间点左右两端轨迹的表达式了，同时我们将轨迹相关的表达式都移到等式左边的话，右边就是 b 矩阵对应的元素。
首先中间位点需要满足以下约束，也就是该点如果作为前一段轨迹的终点，位置应该就是提供的中间位点的位置：
此时跟 
无关，那么我们可以令 
的第一行(C++索引为0)元素为0，就有：
之后根据最优条件理论我们可以知道，如果我们的输入是轨迹的 s 阶导数，那么其 2s-d-1 阶导数也都是连续可导的，接下来我们来写相应的表达式满足这个条件。
首先是轨迹在中间位点的位置是要连续的，那么就有前一段轨迹的终点位置等于后一段轨迹的起点位置：
移一下项就有：
其中：
我们再具体考虑速度，也就是轨迹在中间位点的速度也是连续的：
其中：
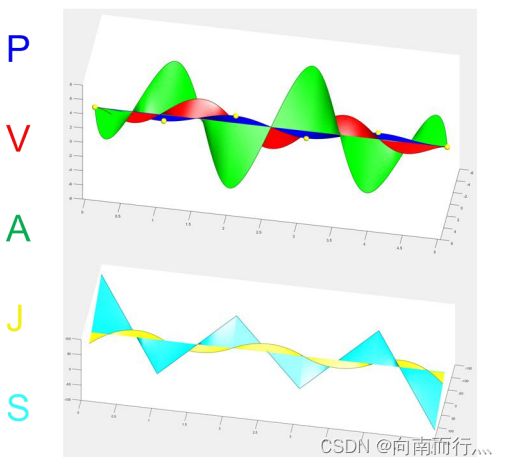
最优条件理论说了，如果我们生成的是jerk轨迹，那么在中间位点上直到snap都是连续的，如下图所示：
那么我们就可以依此类推，最终得到：
![\large \begin{bmatrix} D_T^1 & 0_{M \times \bar{d_1}} \end{bmatrix}^T=[IntermediatePos, 0, 0, 0, 0, 0]^T](http://img.e-com-net.com/image/info8/e9c944fff26d4141bab457e0b833bcb7.gif){kind=small}
那么随着中间点增多，我们就可以用循环把这些元素依次填进去：
for (int i=1; i < pieceNum ; i++){
double t(timeAllocationVector(i-1));
Eigen::MatrixXd F_i(6,6), E_i(6,6);
Eigen::Vector3d D_i(intermediatePositions.transpose().row(i-1));
E_i << 1, t, pow(t, 2), pow(t, 3), pow(t, 4), pow(t, 5),
1, t, pow(t, 2), pow(t, 3), pow(t, 4), pow(t, 5),
0, 1, 2*t, 3*pow(t, 2), 4*pow(t, 3), 5*pow(t, 4),
0, 0, 2, 6*t, 12*pow(t, 2), 20*pow(t, 3),
0, 0, 0, 6, 24*t, 60*pow(t, 2),
0, 0, 0, 0, 24, 120*t;
F_i << 0, 0, 0, 0, 0, 0,
-1, 0, 0, 0, 0, 0,
0, -1, 0, 0, 0, 0,
0, 0, -2, 0, 0, 0,
0, 0, 0, -6, 0, 0,
0, 0, 0, 0, -24, 0;
int j = 6 * (i-1);
M.block(3+6*(i-1), j + 6, 6, 6) = F_i;
M.block(3+6*(i-1), j, 6, 6) = E_i;
b.block(3+6*(i-1), 0, 6, 3) << D_i(0), D_i(1), D_i(2),
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0;
}最后，我们就得到了最终的 M 矩阵和 b 矩阵， 接下来通过对 M 矩阵求逆就可以解出系数矩阵 c：
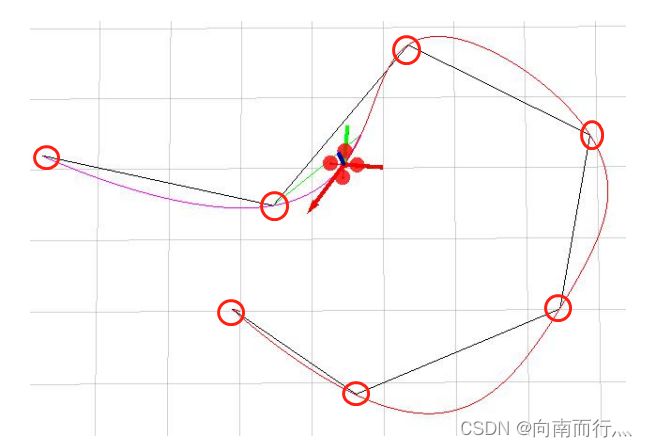
coefficientMatrix = M.inverse() * b;至此，完成作业的代码已经编写完成，其最终效果和实现最小jerk轨迹函数的完整代码如下：
void minimumJerkTrajGen(
// Inputs:
const int pieceNum,
const Eigen::Vector3d &initialPos,
const Eigen::Vector3d &initialVel,
const Eigen::Vector3d &initialAcc,
const Eigen::Vector3d &terminalPos,
const Eigen::Vector3d &terminalVel,
const Eigen::Vector3d &terminalAcc,
const Eigen::Matrix3Xd &intermediatePositions,
const Eigen::VectorXd &timeAllocationVector,
// Outputs:
Eigen::MatrixX3d &coefficientMatrix)
{
// coefficientMatrix is a matrix with 6*piece num rows and 3 columes
// As for a polynomial c0+c1*t+c2*t^2+c3*t^3+c4*t^4+c5*t^5,
// each 6*3 sub-block of coefficientMatrix is
// -- --
// | c0_x c0_y c0_z |
// | c1_x c1_y c1_z |
// | c2_x c2_y c2_z |
// | c3_x c3_y c3_z |
// | c4_x c4_y c4_z |
// | c5_x c5_y c5_z |
// -- --
// Please computed coefficientMatrix of the minimum-jerk trajectory
// in this function
// ------------------------ Put your solution below ------------------------
Eigen::MatrixXd M = Eigen::MatrixXd::Zero(6 * pieceNum , 6 * pieceNum );
Eigen::MatrixXd b = Eigen::MatrixXd::Zero(6 * pieceNum , 3);
Eigen::MatrixXd F_0(3,6);
F_0 << 1, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0,
0, 0, 2, 0, 0, 0;
M.block(0, 0, 3, 6) = F_0;
b.block(0, 0, 3, 3) << initialPos(0), initialPos(1), initialPos(2),
initialVel(0), initialVel(1), initialVel(2),
initialAcc(0), initialAcc(1), initialAcc(2);
for (int i=1; i < pieceNum ; i++){
double t(timeAllocationVector(i-1));
Eigen::MatrixXd F_i(6,6), E_i(6,6);
Eigen::Vector3d D_i(intermediatePositions.transpose().row(i-1));
E_i << 1, t, pow(t, 2), pow(t, 3), pow(t, 4), pow(t, 5),
1, t, pow(t, 2), pow(t, 3), pow(t, 4), pow(t, 5),
0, 1, 2*t, 3*pow(t, 2), 4*pow(t, 3), 5*pow(t, 4),
0, 0, 2, 6*t, 12*pow(t, 2), 20*pow(t, 3),
0, 0, 0, 6, 24*t, 60*pow(t, 2),
0, 0, 0, 0, 24, 120*t;
F_i << 0, 0, 0, 0, 0, 0,
-1, 0, 0, 0, 0, 0,
0, -1, 0, 0, 0, 0,
0, 0, -2, 0, 0, 0,
0, 0, 0, -6, 0, 0,
0, 0, 0, 0, -24, 0;
int j = 6 * (i-1);
M.block(3+6*(i-1), j + 6, 6, 6) = F_i;
M.block(3+6*(i-1), j, 6, 6) = E_i;
b.block(3+6*(i-1), 0, 6, 3) << D_i(0), D_i(1), D_i(2),
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0;
}
double t(timeAllocationVector(pieceNum-1));
Eigen::MatrixXd E_M(3,6);
E_M << 1, t, pow(t, 2), pow(t, 3), pow(t, 4), pow(t, 5),
0, 1, 2*t, 3*pow(t, 2), 4*pow(t, 3), 5*pow(t, 4),
0, 0, 2, 6*t, 12*pow(t, 2), 20*pow(t, 3);
M.block(6 * pieceNum -3, 6 * (pieceNum - 1), 3, 6) = E_M;
b.block(6 * pieceNum -3, 0, 3, 3) << terminalPos(0), terminalPos(1), terminalPos(2),
terminalVel(0), terminalVel(1), terminalVel(2),
terminalAcc(0), terminalAcc(1), terminalAcc(2);
coefficientMatrix = M.inverse() * b;
// ------------------------ Put your solution above ------------------------
}